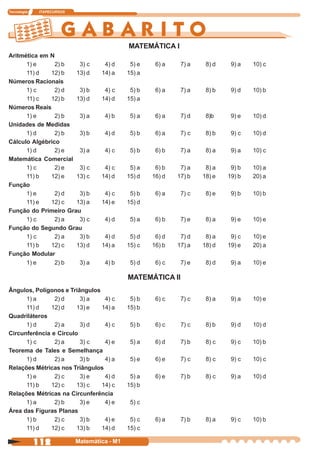
O documento apresenta um resumo de conceitos fundamentais de matemática, dividido em duas partes:
1) Aritmética em N, que inclui tópicos como sistema de numeração decimal e não decimal, operações algébricas e funções;
2) Geometria Plana, abordando conceitos geométricos como ângulos, polígonos, círculos e suas propriedades.




































![Tecnologia ITAPECURSOS
1) Sejam as funções reais f e g definidas por f(x) = 2x – 3 e g(x) = x2 + 1. Calcule:
a) (gof)(1) c) (gof)(x)
b) f(g(2)) d) f(g(x))
Solução:
a)
b)
c) símbolo (gof)(x) = g(f(x)) e aqui se pede para substituir, na função g, o x por f(x).
Portanto:
g(f(x)) = [f(x)]2 + 1 = (2x – 3)2 + 1 = 4x2 – 12x + 10
d) f(g(x)) = 2g(x) – 3 = 2(x2 + 1) – 3 = 2x2 – 1
2) Se f(x) = 2x – 1 e g(x) = 3x + K, ache K para que (fog)(x) = (gof)(x).
Solução:
f(g(x)) = 2g(x) – 1 = 2(3x + K) – 1 = 6x + 2K – 1
g(f(x)) = 3f(x) + K = 3(2x – 1) + K = 6x – 3 + K
Como fog = gof, teremos: 6x + 2K – 1 = 6x – 3 + K e daí, K = –2.
3) Sejam as funções f(x) = e g(x) = 2x + 3.
a) Determine o domínio de f e o de g.
b) Determine o domínio de fog e gof.
Solução:
a) D(f) = {x ∈ R: x ≠ 2}
D(g) = R
b) Domínio de fog.
Como já dissemos, o domínio de fog é formado pelos elementos do domínio de g para os quais g(x) está no
domínio de f. Logo:
x ∈ D(g) → x ∈ R
g(x) ∈ D(f) → 2x + 3 ≠ 2 ; x ≠ – ½
Então, D(fog) = {x ∈ R: x ≠ – ½ }
Matemática - M1 37](https://image.slidesharecdn.com/apmatemticam1-111212030220-phpapp01/85/Ap-matematica-m1-37-320.jpg)




















































![Tecnologia ITAPECURSOS
8) (PUC-MG) Considere f (x) = x - 3 e f [g(x)] = 3x + 4. O valor de g (3) é:
a) 6 b) 8 c) 10 d) 13 e) 16
9) (IH-MG) Na figura abaixo estão esboçados os gráficos das funções f(x) e g(x), definidas no intervalo [-4,5]. O
conjunto {x ∈ R / f(x) - g(x) ≤ 0} é:
a)
10) (UFOP-MG) Se , então f(x) – g(x) é:
a) 2x3 - 2x b) 2x c) -2 d) 0 e) 1
11) (FUVEST) A figura ao lado representa o gráfico
de uma função da forma para
-1 ≤ x ≤ 3.
Pode-se concluir que o valor de b é
a) –2 b) –1 c) 0 d) 1 e) 2
12) (FCMMG) Sejam
Então, f(g(x)) e g(f(x)) são, respectivamente, iguais a:
a) 0 e 0 b) 0 e 1 c) 1 e 0 d) 1 e 1
13) (M. Campos-MG) Sendo f -1(x) a função inversa de é igual a:
a) -1 b) 1 c) 2 d)
14) (UFOP-MG) Se f(x) = 1 - 3x e g(x) = k – x, então a solução da equação (fog) (2) = -12 é:
a) -17 b) -7 c) 11/3 d) 22/5 e) 19/3
15) (CEFET-MG) Se f (0) = 2 e f (n + 1) = [f (n)] 2 + 2, então f (2) é igual a:
a) 22 b) 26 c) 36 d) 38 e) 44
FUNÇÃO DO PRIMEIRO GRAU
1) (FCMMG) Suponha que a temperatura T do ar exalado através das narinas varie com a temperatura ambiente
A, obedecendo à seguinte lei T = b + m.A. Se T = 13 quando A = 5 e T = 17 quando A = 10, então o valor
de A para que T = 20,2 é:
a) 11 b) 12 c) 14 d) 15
98 Matemática - M1](https://image.slidesharecdn.com/apmatemticam1-111212030220-phpapp01/85/Ap-matematica-m1-98-320.jpg)


![Tecnologia ITAPECURSOS
11) (Univ. Itaúna-MG) O conjunto solução da 17) (PUC-MG) Duas funções, f e g, são dadas por
seus gráficos abaixo.
desigualdade é:
a) [ -2, 2 ] c) ]-∞, -2[
b) ] -2, 2 [ d) ]2,+∞ [
12) (PUC-MG) A soma dos números inteiros que não
pertencem ao domínio de é:
a) –2 b) –1 c) 0 d) 1 e) 2
13) (PUC-MG) Se x2 ≥ 9 então: A solução da inequação é:
14) (UFMG) Seja M o conjunto dos números naturais
tais que 2n2 - 75n + 700 ≤ 0.
Assim sendo, é CORRETO afirmar que:
a) apenas um dos elementos de M é múltiplo de 4.
b) apenas dois dos elementos de M são primos.
18) (N.Paiva-MG) Um carrinho de montanha russa
c) a soma de todos os elementos de M é igual a 79. desliza numa trajetória cuja equação é
d) M contém exatamente seis elementos. y = x2 - 5x - 6. Suponha que o carrinho parte do
ponto A de coordenadas (7,8) e desce até o ponto
15) (UEMG) O maior subconjunto de R para o qual B de ordenada -6. A maior distância hori-zontal
percorrida pelo carrinho em metros é:
está definida a função está
a) 2 b) 4 c) 6 d) 7
representado em:
19) (PUC-MG) Um terreno tem a forma de um
triângulo retângulo com lados medindo,
respectivamente, 60 m, 80 m e 100 m. A medida
da área do maior barracão retangular que se pode
construir nesse terreno, na posição indicada na
figura, em m2, é:
a) 850
b) 900
16) (Fund. João Pinheiro-MG) Certa noite, observou- c) 950
se que a temperatura em Diamantina, dada em d) 1.100
graus centígrados, obedeceu à lei T(h) = h2 - 7h e) 1.200
+ 18, em que h é medido em horas e T(h) é a
temperatura correspondente. Durante um deter- 20) (PUC-MG) O gráfico representa as funções
minado intervalo de tempo, essa temperatura y = ax2 + bx + c e y = mx + n.
manteve-se abaixo de 8°C. Assim sendo, a Se A (-2,4) e B (1,1) são seus pontos de interseção,
duração desse intervalo de tempo foi de: o valor da expressão 4a – 2b + c + m + n é:
a) 2 horas a) 5
b) 3 horas b) 7
c) 4 horas c) 8
d) 5 horas d) 10
e) 6 horas e) 13
Matemática - M1 101](https://image.slidesharecdn.com/apmatemticam1-111212030220-phpapp01/85/Ap-matematica-m1-101-320.jpg)

![Tecnologia ITAPECURSOS
MATEMÁTICA II
ÂNGULOS, POLÍGONOS E TRIÂNGULOS
1) (PUC-MG) Na figura, AB = AC, BD é bissetriz do
ângulo B e a medida do ângulo DBC é 33°30’. A 6) (FAFEOD-MG) Na figura a seguir, o triângulo ABC
medida do ângulo A, em graus, é: é isósceles, com AB = AC, e nele está inscrito o
triângulo eqüilátero DEF:
a) 46
b) 50
c) 56
d) 62
e) 67
2) (Univ. Itaúna-MG) Observe a figura.
Se as medidas, em graus, dos ângulos BDF e
No triângulo eqüilátero da figura, DE // AB e AE é DEA são, respectivamente, 50 e 80, então é
bissetriz de A . Então o valor de a, em radianos, CORRETO afirmar que a medida, em graus, do
é: ângulo CFE é igual a:
a) π / 3 a) 45 b) 55 c) 65 d) 75
b) π / 4
c) π / 6 7) (PUC-MG) Dois lados de um triângulo medem,
respectivamente, 4 m e 10 m. Os possíveis valores
d) π / 2 da medida do terceiro lado, em metros, oscilam
3) (FAFEOD-MG) Na figura abaixo, os segmentos no intervalo:
de reta AB, AC e CD são congruentes, b é um a) ] 6,10 [
ângulo externo, e a um ângulo interno do triângulo b) ] 4,10 [
ABD.
c) ] 6,14 [
Assinale a opção que contém a expressão correta
de b em termos de a: d) ] 10,14 [
e) ] 4,14 [
a) β = 3α.
b) β = 2α. 8) (UERJ) Dispondo de canudos de refrigerantes,
c) β = α/2. Tiago deseja construir pirâmides. Para as arestas
laterais, usará sempre canudos com 8 cm, 10
d) β = 2α/3. cm e 12 cm de comprimento. A base de cada
e) β = 3α/2. pirâmide será formada por 3 canudos que têm a
mesma medida, expressa por um número inteiro,
4) (N.Paiva-MG) A diferença entre o número de
diferente das anteriores. Veja o modelo:
diagonais de dois polígonos é 8. Se os dois
polígonos tiverem o número de lados expresso A quantidade de pirâmides de bases diferentes
por dois números inteiros consecutivos, a soma que Tiago poderá construir é:
do número de lados dos dois polígonos é: a) 10
a) 9 b) 17 c) 19 d) 21 b) 9
c) 8
5) (UFMG) Observe a figura.
d) 7
Nessa figura, AD = BD, 9) (UFPE) Na figura abaixo, BC e AC são bissetrizes
ACB = 60° e DAC é o dos ângulos DBE e DAB, respectivamente. Se o
dobro de ABD. ângulo ACB mede 21°30’, qual a medida em graus
do ângulo ADB?
A razão é igual a:
a) 43 d) 44
b) 41 e) 42
c) 40
Matemática - M1 103](https://image.slidesharecdn.com/apmatemticam1-111212030220-phpapp01/85/Ap-matematica-m1-103-320.jpg)