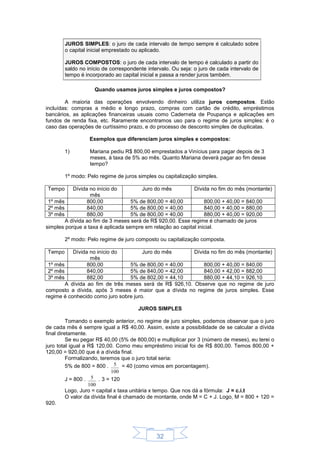
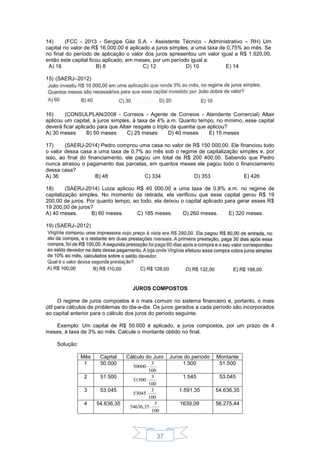
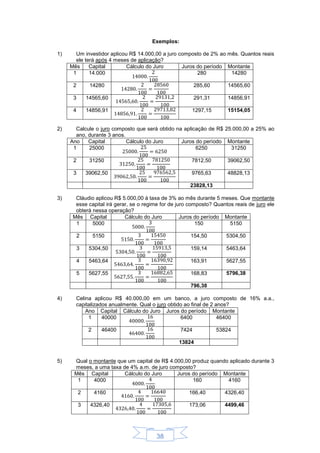
1) O documento descreve sequências e progressões aritméticas, definindo-as como listas ordenadas de números que seguem uma regra. 2) Ele fornece exemplos de sequências comuns e explica como encontrar a expressão geral de uma sequência e calcular termos específicos. 3) O documento também explica o que é uma progressão aritmética e fornece a fórmula para calcular qualquer termo de uma progressão aritmética.