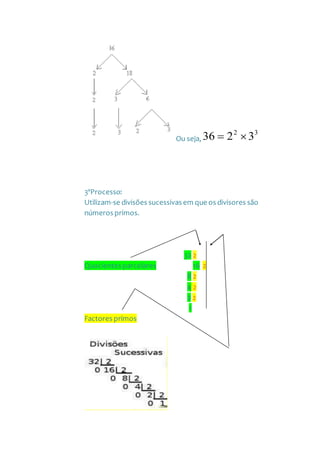
O documento aborda conceitos fundamentais de números primos e compostos, destacando suas definições e propriedades, incluindo a decomposição em fatores primos. Também discute operações básicas como adição, subtração, multiplicação e divisão de números racionais, apresentando regras e propriedades associadas. Além disso, menciona o máximo divisor comum (m.d.c) e o mínimo múltiplo comum (m.m.c), bem como a representação de números na reta numérica.

1. Introdução:
 1.Números primos e números
compostos;
 2.Adição e subtracção com
representação na recta numérica;
 3.Multiplicação e divisão em q –
propriedades;
 4.Potências, raiz quadrada e raiz
cúbica;
1.Números primos e númeroscompostos:
Paramelhor identificação de números primos e números
compostos deve-serecordar o conceito de divisor e de um
número natural.

2. No conjunto dos números naturais tem-se:
Múltiplos de um número natural são todos os números que se
obtêm multiplicando esse número porcadaum dos números
naturais.
Divisores de umnúmero natural são todos os números naturais que
o dividem exactamente.
Decomposição e factores primos:
Um número natural diferente de 1 diz-se:
 Número primo se e só tem exactamente dois divisores: o 1 e o
próprio número;
Ex:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,5961,67,71,73,79,83,89,9
7...
Nota: Para melhoridentificação de números primos e
números compostos deve-se recordaro conceito de divisor
e de um número natural.
 Número composto se e só se tem mais de dois divisores.
Ex:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28,
30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51,
52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74,
75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94,
95, 96, 98, 99, 100….etc.
Nota: o número 1 não é número primo nem número composto.

3. Dado um número naturalmaior que 1 e que não seja
número primo, é possívelrepresentá-lonaformade
produto cujos factores sejam números primos, ouseja, é
possíveldecompô-lo num produtode número primos.
Ex:
1ºProcesso:
Começa-se por transformar 36num produto de dois
factores .
Por exemplo, 9436  .
Os factores 4 e 9 não são primos. Mas, 224  e
339  .
332236  OU
22
3236 
2ºProcesso:
Partindo da decomposição, 18236 
Como 2 é número primo e 18é número composto, tem-se:

4. Ou seja,
32
3236 
3ºProcesso:
Utilizam-se divisões sucessivas em que os divisores são
números primos.
32 2
Quocientes parcelares 16 2
8 2
4 2
2 2
1
Factores primos

5. Daqui resultaque: 3222222  OU
5
2
Propriedade:
Qualquer número naturalcompostopode ser representado
como produto de números primos. Estadecomposição é
única, não considerando a ordem dos factores.
Estapropriedade é designada por Teorema fundamentalda
aritmética.
Máximo
divisor comum (m.d.c)e mínimo múltiplo comum(m.m.c)
Regras práticas:
1.Paradeterminar o m.d.c. de dois oumais números:
1º.Descompor os números dados em factores primos;
2º.Escolher os factores primos comuns elevados ao menor
expoente;
3º.O produto desses factores é o máximodivisor comum.
2.Paradeterminar o m.d.c. de dois oumais números:
1º.Decomporos númerosdados em factores primos;
2º.Escolher os factores primos comuns e não comuns
elevados maior expoente;
3º.O produto desses factores é o mínimo múltiplocomum.

6. Propriedade:
O produto do mínimo múltiplo comumpelo máximo divisor comum
de dois naturais é igual ao produto entre eles.
Recorda:
Dois números naturais a e b dizem-se primosentre si se m.d.c.
(a,b)=1.
2.Adição e subtracção comrepresentação narectanumérica
2.1.Representação de números racionais narectanumérica
São várias as situações em que há necessidade de indicar se um
certo número está“acimade zero”ou“abaixo de zero”.
Recorda:
Conjuntos numéricos
O conjunto dos números inteiros representa-se por Z.

7. Z =  ,...4,3,2,1,0,1,2,3,4,5,6..., 
O conjunto dos números inteiros negativos é Z

.
Z

=  1,2,3,4,5,6..., 
O conjunto dos números inteiros positivos é representado por
Z 
.
Z 
= ,...4,3,2,1 
Números naturais
0 1 2 3 4 5 6 7 8
Númerosinteiros númerosinteiros
Negativos positivos
Se reunirmos o conjunto dos números fraccionários obtemos o
conjunto dos númerosracionais que se representapor Q.
O conjunto dos números que podem ser representados por
uma fracção de números inteiros chama-se conjunto dos
númerosracionais e representa-se por Q.
Q

: Números racionais positivos;
Q

: Números racionais negativos.
Na rectanumérica, acada ponto correspondente um númeroe
a cada número corresponde um pontodarecta.

8. Ao número correspondente aum ponto darectadá-se o nome
de abcissa desse ponto.
Abcissaé a coordenadahorizontalde um referencial plano
de coordenadas cartesianas. Representando essereferencial
sob a formade um gráfico, obtemos aabcissa(x) medindo a
distância do ponto observadoao eixo das ordenadas (y),
perpendicular ao eixo das abcissas.
As abcissas dos pontos assinalados são -3, -1.5, 0 e 2.
No caso geraltem-se:
Valor absoluto ou módulo de um número racional a é igual à
distância do ponto que lhe corresponde, narectanumérica, à
origem e representa-se por a .
Dois números racionais diferentes de zero são simétricosse e
só se têm sinais diferentes (um positivo e outro negativo) e
têm o mesmo valor absoluto.
O número racional 0 .
Comparação de númerosracionais

9. 0 é menor que qualquer númeropositivo.
0é maior que qualquer número negativo.
Qualquer número positivo é maior que qualquer
número negativo.
Dados dois números positivos é maior o que tiver
maior valor absoluto.
Dados dois números negativos é maior o que tiver
menor valor absoluto.
2.2.Adição em Z
A soma de númeroscom o mesmo sinal é um número com igual
sinal e cujo valor absoluto é igual à somados valores absolutos
das parcelas.
A soma de números não simétricos com sinais diferentes é o
número que satisfaz as condições:
O seusinal é o da parcelade maior valor absoluto;
O seuvalor absoluto é igual à diferençados valores
absolutos das parcelas.
A soma de dois númerossimétricos é zero.
    0 aaaa
2.3.Adição em Q

10. As regras paraadicionar números inteiros e as propriedades
da adição em Z continuam válidas em Q.
Recorda
Paraadicionar ousubtrair números representados naforma
de fracção começa-se por representa-los através de fracções
com igual denominador e adicionam-se ousubtraem-seos
numeradores.
Propriedadesda adição em Q
Todas as propriedades daadição que conheces em Z
continuam válidas em Q.
Assim, tem-se:
Propriedades da adição em Q
Comutativa
abba 
Associativa    cbacba 
Existênciade elemento
neutro.
0-elemento neutro.
aaa  00
Existênciade elemento
simétrico
Todo o número racional
tem simétrico.
(-a é o simétrico de a)
2.4.Subtração em Q
Parasubtrair dois númerosracionais adiciona-se ao aditivo o
simétrico do subtractivo.

11. )( baba 
0 1 2 3 4 5 6 7 8 N
Z 
Assim, na escritados números inteiros positivos não é necessário
escrever o sinal+.Por exemplo, emvez de +3escreve-se 3.
3.Multiplicação e divisão em q – propriedades
3.1.Multiplicação em Q
Recorda
Sendo a,b,c e d números naturais tem-se:
.
db
ca
d
c
b
a



Sendo q um número racional negativo tem-se:
00'0  qq
Produto de um número natural por um racional

12. O produto de um número natural n por um racional q
é a soma de n parcelas iguais a q.
Assim, tem-se: q+q+…+q=nxq (ou qxn)
n parcelas
No caso geral, tem-se:
O produto de um número natural n por um número
racional q e representa-se por nxq e por qxn.
Prova-se que: )()( qnnqqn 