Mat exercicios resolvidos

(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2007 –MATEMÁTICA

MATEMÁTICA Assim, a arrecadação mensal é dada por:
1) primeiro mês: R$9000,00
QUESTÃO 31 2) segundo mês: R$16200,00
3) terceiro mês: R$32400,00
Analise as alternativas abaixo e marque a correta.
4) quarto mês: R$21600,00
a) Se B = {m ∈ N | m 2 < 40} , então o número de elementos do Total: R$79200,00
conjunto B é 6. Dividindo o total por 10000, notamos que, se cada camiseta fosse
1 1 vendida por R$7,92, o mesmo montante teria sido arrecadado. Logo, a
b) Se α = + , então α ∈ [( R − Q) ∩ ( R − Z )] alternativa correta é a alternativa A.
2 −1 2 +1
c) Se c=a+b e b é divisor de a, então c é múltiplo de a,
necessariamente. QUESTÃO 33
d) Se A =]1, 5[ e B =] − 3, 3[ , então B − A =] − 3, 1[ . Considere no Plano de Argand-Gauss os números complexos z1 = –x
– 2i, z2 = –2i, z3 = –2 + 3i e z4 = x + yi, onde x e y são números reais
Resolução Alternativa B quaisquer e i2 = –1.
Analisando cada alternativa: Sobre o conjunto desses números complexos que atendem
a) Observe que B = {0,1,2,3,4,5,6}, ou seja, B possui 7 elementos. simultaneamente às condições
Assim, a alternativa está incorreta.
I) Re( z1 ⋅ z2 ) ≤ Im( z1 ⋅ z2 )
1 1 2 +1+ 2 −1 2 2
b) α = + = = =2 2. II) | z3 + z4 |≤ 2
2 −1 2 +1 ( )(
2 −1 2 +1) 2 −1
é correto afirmar que
Assim, temos que α é um número irracional, ou seja, não é racional a) representa uma região plana cuja área é menor que 6 unidades de
nem inteiro. Assim, α ∈ (IR − Q) ∩ (IR − Z) . área.
b) possui vários elementos que são números imaginários puros.
c) Se c = a + b e b é divisor de a, segue que a = k.b, para algum inteiro c) possui vários elementos que são números reais.
k. Assim, temos que c = k.b + b, ou seja, c = b(k+1). Portanto, o d) seu elemento z de menor módulo possível possui afixo que
número c é múltiplo de b, o que não significa que c seja múltiplo de a. pertence à reta (r) 3x + 2y = 0
Alternativa incorreta.
d) Seja A = ]1;5[ e B = ]-3;3[. Assim, B – A = {x / x está em B e x não Resolução Alternativa D
está em A} = ]-3;1] ≠ ]-3;1[. Alternativa incorreta. ⎧z1 = − x + 2i
⎪
⎨ ⇒ z1 ⋅ z2 = ( − x + 2i ) ⋅ (2i ) = −4 − 2 xi
OBS: no item (a), admitimos que 0 é um número natural, embora em ⎪z2 = 2i
⎩
Análise Matemática tal número seja considerado inteiro, e não natural. A condição I então fica:
QUESTÃO 32 Re( z1 ⋅ z2 ) ≤ Im( z1 ⋅ z2 ) ⇒ −4 ≤ −2 x ⇒ x ≤ 2
Um fabricante de camisetas que pretendia vender seu estoque no A condição II, por sua vez, pode ser escrita como:
prazo de 4 meses, mantendo o preço de cada camiseta, obteve o | z3 + z4 |≤ 2 ⇒| z4 − ( − z3 ) |≤ 2 ⇒| z4 − (2 − 3i ) |≤ 2
seguinte resultado:
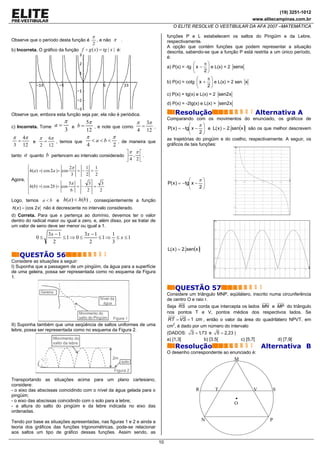
- no primeiro mês, vendeu 10% de seu estoque; Observe que esta condição nos diz que os números z4 que satisfazem
- no segundo, 20% do restante das mercadorias; e a esta condição são aqueles cuja distância até o número complexo (–
- no terceiro, 50% do que sobrou z3) = 2 – 3i é menor ou igual a 2, ou seja, trata-se de um círculo de
Ao ver que sobraram 3.600 camisetas, no quarto mês, o fabricante centro (2,–3) e raio 2.
1 No plano de Argand-Gauss, temos:
reduziu o preço de cada uma em 33 % , conseguindo assim liquidar
3 y
todo seu estoque e recebendo R$ 21.600,00 pelas vendas deste mês.
É correto afirmar que o fabricante
a) arrecadaria a mesma importância total, durante os 4 meses, se
cada camiseta fosse vendida por x reais, x∈[7,8] 2
b) tinha um estoque que superava 834 dúzias de camisetas.
c) no terceiro mês, vendeu uma quantidade de camisetas 200% a mais
x
que no segundo mês.
d) no primeiro mês, recebeu mais de R$ 9.000,00
Resolução Alternativa A
Seja x o total de camisetas do estoque. De acordo com o enunciado,
temos que: –3
- No primeiro mês foram vendidos 10% do estoque, restando então
90%.x.
- No segundo mês o total de vendas foi de 20% do restante, ou seja,
sobra no estoque um total de 80%.90%.x = 72%.x. A intersecção das condições I e II será então tomar os pontos do
- Ao final do terceiro mês, ele vende 50% da mercadoria que está no círculo sombreado acima que têm parte real menor ou igual a 2. Isso
estoque, ou seja, sobra no estoque 50%.72%.x = 36%.x. corresponde à metade da esquerda desse círculo:
Portanto, no início do quarto mês o vendedor tem 36% do seu estoque
inicial disponível para vendas, num total de 3600 camisetas. Logo,
y
36%.x = 3600 ⇒ x = 10000 camisetas.
Observe que:
1) primeiro mês: 1000 camisetas vendidas
2) segundo mês: 1800 camisetas vendidas 2
3) terceiro mês: 3600 camisetas vendidas x
1
Para o quarto mês, ele fez uma redução de 33 % nos preços das
3
camisetas, ou seja, reduziu 1/3 do preço, conseguindo vender todas
as que restavam no estoque e arrecadando R$21.600,00 por elas.
Seja p o preço unitário por camiseta antes da redução de preços. Do –3
enunciado, temos:
2 2
⋅ p ⋅ 3600 = 21600 ⇒ ⋅ p = 6 ⇒ p = 9
3 3 a) Falsa. A área desse semicírculo de raio 2 será dada por:

1

(19) 3251-1012

1 distância permanece igual a 35 m. Assim, a alternativa B também está
S = π 22 = 2π ≈ 6,28 > 6 correta.
2 c) A distância total percorrida será a soma dos termos de uma PA, que
b) Falsa. O número –3i é o único número complexo imaginário puro ⎛ 2a1 + (n − 1)r ⎞
nessa região, conforme o gráfico. pode ser calculada por Sn = ⎜ ⎟ r . Assim, temos que,
⎝ 2 ⎠
c) Falsa. Não há intersecção com o eixo x (eixo real), logo não há
nenhum número real nesse semicírculo. após 10 segundos, o cão terá percorrido uma distância de
d) Verdadeira. Os elementos do círculo (condição II) que são o de (2 ⋅ 2 + 9 ⋅ 2).10
S10 = = 110 m, enquanto o gato terá percorrido
menor e o de maior módulo podem ser obtidos geometricamente 2
traçando a reta que liga o centro (2,–3) à origem:
(2 ⋅ 3 + 9 ⋅ 1).10
uma distância de S10 = = 75 m. Assim, após os 10
y 2
segundos o cão terá percorrido exatamente 110 m = 35 + 75, ou seja,
ele alcançará o gato. Assim, a alternativa C também está correta.
d) No oitavo segundo, levando em consideração que o gato percorre
distâncias em PA:
2 an = a1 + (n − 1) ⋅ r ⇒ a8 = 3 + 7 = 10
Assim, o gato percorre 10 m, e não 14. Assim, a alternativa D está
x incorreta.
A
QUESTÃO 35
Sejam as seqüências de números reais (-3, x, y,…) que é uma
progressão aritmética de razão r, e (x, y, 24,...) que é uma progressão
geométrica de razão q.
–3 O valor de
r
pertence ao intervalo:
q
⎡ 1⎡ ⎡1 ⎡
a) ⎢0, ⎢ b) ⎢ ,1⎢ c) [1,2[ d) [ 2,3[
B ⎣ 2⎣ ⎣2 ⎣
Resolução Alternativa C
Por hipótese, temos:
PA ( -3,-3+r,-3+2r,...)
O ponto A é o de menor módulo e o ponto B é o de maior módulo. A PG ( x, xq, xq2,...)
Assim, temos as seguintes igualdades:
reta AB tem equação:
x = – 3 + r; y= – 3 + 2r; y = xq; 24 = yq = (– 3 + 2r)q
0 0 1 Assim,
24=(– 3 + 2r).q (1)
2 −3 1 = 0 ⇒ 3 x + 2y = 0 – 3 + 2r = (– 3 + r)q (2)
x y 1 −3 + r −3 + 2r 9
Logo, = ⇔ 4r 2 − 36r + 81= 0 ⇔ (2r − 9)2 = 0 ⇔ r =
Assim, o elemento z de menor módulo possível, cujo afixo −3 + 2r 24 2
corresponde ao ponto A, pertence não só círculo, mas de fato ao
semicírculo considerado, e também pertence á reta 3x + 2y = 0. Substituindo em (1), temos:
9
24 = ( −3 + 2. ). q ⇔ 24 = 6q ⇔ q = 4 .
QUESTÃO 34 2
Um cão e um gato, ambos parados, observam-se a uma distância de 9
r 9
35 m. No mesmo instante, em que o cão inicia uma perseguição ao Portanto, = 2 = = 1,125 .
gato, este parte em fuga. q 4 8
O cão percorre 2 m no primeiro segundo, 4 m no seguinte, 6 m no
terceiro segundo e, assim, sucessivamente. O gato, apavorado,
percorre 3 m no primeiro segundo, 4 m no seguinte, 5 m no terceiro
QUESTÃO 36
segundo e, assim, sucessivamente. Considere π = 3,14 e i = −1 e marque a alternativa correta.
Considerando que os dois animais se deslocam sempre sem a) Se S(x) = x2(x-a) + bx – c, onde a, b, e c são números reais
interrupção em seu movimento e numa trajetória retilínea de mesmo positivos, admite duas raízes simétricas, então
sentido, assinale a alternativa INCORRETA. 1
a) Até o quinto segundo, o cão terá percorrido uma distância igual log a + log = co logb
c
àquela que o separa do gato naquele instante.
b) O polinômio P(x) ao ser dividido por (x-1) deixa resto 6 e ao ser
b) Ao final dos três primeiros segundos, o cão ainda está 35 m distante
dividido por (x+3) deixa resto -2. Se P(x) dividido por Q(x) = x2 + 2x – 3
do gato.
deixa resto R(x), então R(0) = 2P(-3)
c) Em dez segundos, o cão alcançará o gato.
d) No oitavo segundo, o gato percorre 14 metros. c) Se os números complexos 2π, 2i e i-5 são raízes do polinômio A(x)
de coeficientes reais e termo independente nulo, então, o grau de A(x)
Resolução Alternativa D é, necessariamente, um número par maior do que 4
Note que a distâncias percorridas por segundo do cão e do gato são d) Se no polinômio B(x) = x4 + ax3 + bx2 + cx + 16 os coeficientes a, b
progressões aritméticas. Assim: e c são números reais, então as possíveis raízes racionais de B(x)
Cão: (2,4,6,8,10,...) estão entre os divisores de 16, necessariamente.
Gato: (3,4,5,6,7,...)
Analisando cada uma das alternativas, temos:
a) Até o quinto segundo, o cão terá percorrido 2+4+6+8+10 = 30 m, Analisando cada alternativa, temos:
enquanto o gato terá percorrido 3+4+5+6+7 = 25 m, ou seja, o cão a) Correta: Seja S(x) = x3 − ax2 + bx − c um polinômio que admite
percorre 5 m a mais do que o gato. Como a distância entre cão e gato duas raízes simétricas. A partir das relações de Girard:
era, inicialmente, de 35 m, após o quinto segundo essa distância será −a
de 30 m. Assim, a alternativa A está correta. r1 + r2 + r3 = −
=a
b) Ao final dos três primeiros segundos, o cão terá percorrido 12 m,
1
enquanto o gato também terá percorrido a mesma distância. Logo, a Como a soma de duas raízes simétricas é zero, a terceira raiz é o
próprio a. Assim:
2

(19) 3251-1012

S(a) = a3 − aa2 + ba − c = 0 ⇒ c = ab Uma pessoa fará uma viagem e em cada uma de suas malas colocou
um cadeado contendo um segredo formado por cinco dígitos. Cada
Aplicando logaritmo em ambos os lados:
dígito é escolhido dentre os algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Na
c = ab ⇒ log c = log a + logb ⇒ log a − log c = − logb primeira mala, o segredo do cadeado começa e termina com dígito par
1 e os demais são dígitos consecutivos em ordem crescente. Na
⇒ log a + log = co logb segunda mala, o segredo do cadeado termina em dígito ímpar e
c
apenas o 1º e 2º dígitos são iguais entre si.
b) Incorreta: Seja R(x) o resto da divisão de P(x) por x2 + 2x − 3 = Dessa maneira, se ela esquecer:
(x – 1)(x + 3). Assim, existe um polinômio Q(x) tal que a) o segredo do cadeado da primeira mala, deverá fazer no máximo
P(x) = Q(x)(x − 1)(x + 3) + R(x) . (52 x 83 ) tentativas para abri-lo.
Como o grau do polinômio divisor é 2, podemos escrever R(x) = Ax + b) o segredo do cadeado da segunda mala, o número máximo de
B. Pelo teorema do resto, temos: tentativas para abri-lo será de 1890.
P(1) = R(1) = 6 ⇒ A + B = 6 c) apenas os três dígitos consecutivos em ordem crescente do
P(−3) = R(−3) = −2 ⇒ −3A + B = −2 cadeado da primeira mala, ela conseguirá abri-lo com, no máximo, 8
Resolvendo o sistema, encontramos R(x) = 2x + 4. tentativas.
Assim, R(0) = 4, enquanto 2.P(-3) = -4. d) apenas os dois primeiros dígitos do cadeado da segunda mala,
c) Incorreta: Seja A(x) um polinômio com coeficientes reais. Pelo deverá tentar no máximo 10 vezes para abri-lo.
teorema das raízes complexas, se os números 2i e i – 5 são raízes de Resolução Alternativa C
A(x) então os números conjugados -2i e – i – 5 também são raízes. Pelo enunciado, temos:
Como 2π é raiz e o termo independente sempre é nulo, temos que 0 1) Primeira mala: primeiro e último algarismos são pares, os outros
também é raiz, e o grau de A(x) é, no mínimo, 6. Entretanto, não são dígitos consecutivos em ordem crescentes.
podemos afirmar nada com relação às multiplicidades de cada raiz, Nesse caso, note que temos 5 possibilidades para o primeiro
muito menos que as únicas raízes são essas; logo, não podemos algarismo, 5 possibilidades para o último, 8 possibilidades para o
garantir que o grau sempre será par. segundo (uma vez que o segundo número nunca pode ser 8 ou 9) e
d) Incorreta: Observe que uma condição fundamental para que o apenas 1 possibilidade para o terceiro e quarto números, uma vez que
teorema das raízes racionais funcione é que TODOS os coeficientes eles devem estar em ordem crescente. Assim, o total de possibilidades
do polinômio sejam inteiros. Como sabemos que os coeficientes a, b e é dado por 52.8 = 200.
c são reais (não necessariamente inteiros), não podemos afirmar que Assim, a alternativa (a) está incorreta, uma vez que 200 < 52.83. Além
as possíveis raízes racionais de B(x)=x4+ax3+bx2+cx+16 estão entre disso, note que existem apenas 8 seqüências de três números
os divisores de 16. consecutivos montada a partir dos números 0,1,2,3,4,5,6,7,8 e 9, de
modo que se ela se esquecer dos três dígitos consecutivos então ela
QUESTÃO 37 precisará apenas de 8 tentativas para abrir a mala.
2) Segunda mala: último algarismo ímpar, com apenas o primeiro e
20
⎛1 3⎞ segundo algarismos iguais entre si.
Sabendo-se que x0 = −i , x1 = 3 e x2 = ⎜ + i ⎟ são raízes de
⎜2 2 ⎟ Nesse caso, existem 5 possibilidades para o último número, 9
⎝ ⎠ possibilidades para o primeiro (que não pode ser igual ao último, uma
P ( x ) = x 6 − 3 x 5 + x 4 − 4 x 3 + 3 x 2 − ax + 3 , onde i é a unidade imaginária vez que apenas o primeiro e o segundo são iguais), 1 possibilidade
e a é número real, marque a alternativa FALSA. para o segundo (ele deve ser igual ao primeiro), 8 possibilidades para
a) O número a também é raiz de P ( x ) . o terceiro, que não pode ser igual ao último nem ao primeiro/segundo;
e 7 possibilidades para o quarto, que não pode ser igual a nenhum dos
b) A soma das raízes reais de P ( x ) é um número par. anteriores. Assim, o total de possibilidades é dado por 5.9.1.8.7 =
c) O produto das raízes imaginárias de P ( x ) é diferente de a 2520.
d) P ( x ) é divisível por x 2 + x + 1 . Assim, a alternativa (b) está incorreta, pois 2520 > 1890. Além disso,
note que, caso ela esqueça apenas os dois primeiros dígitos do
Resolução Alternativa C cadeado da segunda mala, então ela não precisará fazer 10 tentativas
Seja P(x) = x6 − 3x5 + x 4 − 4x3 + 3x2 − ax + 3 um polinômio tal para abrir a mala, uma vez que os outros algarismos devem ser
diferentes dos dois primeiros. Assim, na pior das hipóteses, ela deverá
que x0 = -i é raiz. Como a é real, então todos os coeficientes de P(x) fazer 7 tentativas, o que torna a alternativa (d) incorreta.
são reais, daí segue que i também é raiz de P.
P(i) = i6 − 3i5 + i4 − 4i3 + 3i2 − ai + 3 = −1 − 3i + 1 + 4i − 3 − ai + 3 = 0
QUESTÃO 39
⇒ i − ai = 0 ⇒ a = 1 Uma pessoa deve escolher (não importando a ordem) sete, dentre dez
Alternativa A (correta): cartões numerados de 1 a 10, cada um deles contendo uma pergunta
Calculando P(1), temos: P(1) = 1 − 3 + 1 − 4 + 3 − 1 + 3 = 0 diferente. Se nessa escolha houver, pelo menos três, dos cinco
Assim, a = 1 é raiz real de P(x). primeiros cartões, ela terá n formas de escolha.
Alternativa B (correta): Sendo assim, pode-se afirmar que n é um número
As raízes reais de P(x) são 1 e 3, uma vez que temos 6 raízes, sendo a) quadrado perfeito. b) múltiplo de 11.
c) ímpar. d) primo.
4 delas complexas ( x0 , x0 , x2 , x2 ), logo a soma das raízes reais de P é
um número par. Resolução Alternativa B
Alternativa C (FALSA): De acordo com o enunciado, a pessoa deve escolher 3,4 ou 5 cartôes
20 dos 5 primeiros (pelo menos três) e o que falta para completar os 7
⎛1 3⎞ ⎛ 20π ⎞ ⎛ 2π ⎞ 1 3 cartões dos 5 restantes. Como a ordem não importa, temos:
Seja x2 = ⎜ + i ⎟ = cis ⎜ = cis ⎜ =− + i.
⎜2
⎝ 2 ⎟
⎠ ⎝ 3 ⎟⎠ ⎝ 3 ⎟⎠ 2 2 ⎛ 5 ⎞⎛ 5 ⎞ ⎛ 5 ⎞⎛ 5 ⎞ ⎛ 5 ⎞⎛ 5 ⎞
⎜ ⎟⎜ ⎟ + ⎜ ⎟⎜ ⎟ + ⎜ ⎟⎜ ⎟ = 110 , possibilidades para escolher os
⎝ 3 ⎠⎝ 4 ⎠ ⎝ 4 ⎠⎝ 3 ⎠ ⎝ 5 ⎠⎝ 2 ⎠
1 3
Logo, o número x2 = − − i também é raiz de P(x). cartões (que é um múltiplo de 11).
2 2
⎛1 3⎞
QUESTÃO 40
2 2
Assim, x0 ⋅ x0 ⋅ x2 ⋅ x2 = x0 ⋅ x2 = 1⋅ ⎜ + ⎟ = 1 = a
⎝4 4⎠ Analise as proposições seguintes.
Alternativa D (correta): (02) Se 1(1!) + 2(2!) + 3(3!) + … + n(n !) = (n + 1)!− 1 , com
Observando que as raízes de x2 + x + 1 são dadas por x2 e x2 , temos n ∈ {1,2,3,4,…} , então, o valor de
que P(x) é divisível por x2 + x + 1. 1(1!) + 2(2!) + + 10(10!) + 1
é igual a 18.
8!(1 + 2 + 3 + 4 + + 10)
QUESTÃO 38
3

(19) 3251-1012

p
⎛ m ⎞ n 4

(04) O valor de ∑ ⎜ m − 1⎟ é p2 . ∑a 2j b j 1 = ∑ a2 j ⋅ b j 1 ⇔ n = 4 e portanto não podemos afirmar que c21
m =1 ⎝ ⎠ j =1 j =1
4
(08) Uma caixa (I) contém 6 garrafas com rótulo e duas
garrafas sem rótulo; outra caixa (II) contém 4 garrafas
= ∑a
j =1
2j ⋅ bj1
com rótulo e uma sem rótulo. Uma caixa é selecionada
Obs: O produto escalar entre duas n-uplas é definido por:
aleatoriamente e dela uma garrafa é retirada. A
u=(x1,x2,...,xn) e v=(y1,y2,...,yn),
probabilidade dessa garrafa retirada ser sem rótulo é de
22,5%. u,v = ( x1, x2 ,..., xn ),( y1, y 2 ,..., y n ) = x1y1+x2y2+...+xnyn.
(16) Dois dígitos distintos são selecionados aleatoriamente II) A proposição é verdadeira, pois usando o fato de que det(A) =
dentre os dígitos de 1 a 9. Se a soma entre eles é par, a det(At), det(AB)=detA.detB e det(kA)=kndetA, onde n é a ordem da
5 matriz, temos:
probabilidade de ambos serem ímpares é . AYB=2Bt ⇒ det(AYB)=det(2Bt) ⇔ detA.detY.detB=2ndetB,
8
A soma das proposições verdadeiras é igual a: 2n
Logo, det Y =
a)14 b)24 c) 26 d) 30 det A
Resolução Alternativa C Como det A =
1
=
1
= 4 temos:
(02) A proposição é verdadeira, pois por hipótese: det A−1 1
4
1(1)!+ 2(2)!+ ... + 10(10)!+ 1 11!− 1 + 1 11! 990
= = = = 18 2n 2n
8!(1+ 2 + ... + 10) 8!(55) 8!.55 55 det Y = = = 2n − 2
det A 4
(04) A proposição é falsa, pois a soma pedida é a soma das diagonais
III) A proposição é verdadeira:
do Triângulo Aritmético de Pascal. Como a soma das diagonais é dada
Por indução, temos:
p
⎛ m ⎞ ⎛ p + 1⎞
por: ∑ ⎜ ⎟=⎜ ⎟ ⎡1 0 ⎤ ⎡1 0 ⎤ ⎡ 1 0 ⎤
m =1 ⎝ m − 1⎠ ⎝ p − 1⎠ n=2: A2 = ⎢ ⎥.⎢ ⎥=⎢ ⎥
⎣1 1⎦ ⎣1 1⎦ ⎣ 2 1⎦
⎛ p + 1⎞
⎟ = ( p + 1).p ≠ p ;
2
Temos portanto que ⎜ ⎡ 1 0⎤
⎝ p − 1⎠ Assumindo para n=k: Ak = ⎢ ⎥ , temos:
(08) A proposição é verdadeira, pois o evento desejado ocorre quando ⎣ k 1⎦
escolhendo a caixa (I) retiramos uma garrafa sem rótulo ou ⎡ 1 0 ⎤ ⎡1 0 ⎤ ⎡ 1 0⎤ k +1
escolhendo a caixa (II) retiramos uma garrafa sem rótulo. Podemos n=k+1: Ak .A = ⎢ ⎥.⎢ ⎥=⎢ ⎥=A
⎣ k 1⎦ ⎣1 1⎦ ⎣k + 1 1⎦
calcular a probabilidade deste evento ocorrer de
1 2 1 1 9
P= . + . = = 22,5%
2 8 2 5 40 QUESTÃO 42
(16) A proposição é verdadeira, pois se a soma dos dígitos é par, Um suspeito de assaltar dois caixas de um supermercado foi intimado
temos as seguintes possibilidades: a prestar depoimento e fez a seguinte declaração:
Par e Par ou Impar e Impar. “No primeiro caixa foram roubados dois pacotes de notas de 20 reais,
De 1 a 9, temos 4 números pares e 5 ímpares. cinco pacotes de notas de 50 reais e um pacote de notas de 100 reais,
O número de eventos Par e Par é dado por: 4.3=12 e o número de totalizando 100 mil reais. No segundo caixa, foram roubados um
eventos Ímpar e Ímpar é 5.4 = 20. pacote de notas de 20 reais e três pacotes de notas de 100 reais, num
Assim, o espaço amostral é 32 e o número de eventos de interesse é total de 50 mil reais. Os pacotes de notas de mesmo valor tinham a
20 mesma quantidade de notas.
20 5 Cada pacote de notas de 100 reais tinha igual valor de cada pacote de
Logo a probabilidade é = . notas de 50 reais.”
32 8 Diante do depoimento do suspeito, pode-se concluir que:
Assim, a soma pedida é 26. a) ele pode ter falado a verdade.
b) ele falou, necessariamente a verdade.
QUESTÃO 41 c) havia, necessariamente, 940 notas em cada pacote de notas de 20
Analise cada proposição classificando-a como VERDADEIRA ou reais.
FALSA. d) ele mentiu, necessariamente.
I) Sejam as matrizes A = (aij)3xn e B = (bjk)nx4 (n ≥ 1) então a matriz C = Resolução Alternativa A
A·B é tal que o elemento c21 = ∑ a2 j ⋅ b j 1 De acordo com o enunciado, podemos formar o seguinte sistema:
II) A e B são matrizes inversíveis de ordem n. Se AYB = 2Bt, onde Bt é ⎧2.20 x + 5.50 y + 1.100z = 100 000
a transposta de B, o determinante da inversa de A é igual a ¼ e o ⎪
⎨ 1.20 x + 3.100 z = 50 000 onde x é o número de pacotes
determinante de B é igual a ½, então o determinante da matriz Y é ⎪
igual a 2n-2 ⎩ y = 2z
⎡1 0 ⎤ n ⎡ 1 0⎤ *
com notas de 20 reais, y é o número de pacotes com notas de 50 reais
III) Seja a matriz A = ⎢ ⎥ então A = ⎢ n 1⎥ , n ∈ N e z é o número de pacotes com notas de 100 reais.
⎣1 1⎦ ⎣ ⎦ Substituindo a terceira equação na primeira, temos:
É correto afirmar que são verdadeiras
a) todas as proposições b) apenas II e III.
⎧40 x + 600z = 100 000
⎨
c) apenas I e II. d) apenas I e III. ⎩20 x + 300z = 50 000
Resolução Alternativa B Logo, como o sistema é possível (embora indeterminado), o assaltante
I) A proposição é falsa, pois para obter um elemento cij do produto de pode ter falado a verdade.
duas matrizes usamos o produto escalar entre os elementos da linha i
da primeira matriz e os elementos da coluna j da segunda matriz, já QUESTÃO 43
que cada fila forma uma n-upla ordenada com os seus elementos. A circunferência (λ ) x2 + y2 – 2x – 2y + k = 0 passa pelo ponto A(0,1).
Assim, usando as hipóteses da proposição:
Sabendo-se que o ponto P de (λ ) mais próximo da origem coincide
C = (AB)3x4 tem como elemento 21:
n com o baricentro do triângulo MNQ, onde M(0,k), N(2k,0) e Q(xQ,yQ) é
c21= a21b11+a22b21+a23b31+a24b41+...+ a2nbn1= ∑ a2 j b j 1 . correto afirmar que a área do triângulo MNQ é um número do intervalo
j =1
⎡ 3⎡ ⎡3 ⎡ ⎡ 5⎡ ⎡5 ⎡
a) ⎢1, ⎢ b) ⎢ ,2⎢ c) ⎢2, ⎢ d) ⎢ ,3⎢
⎣ 2⎣ ⎣ 2 ⎣ ⎣ 2⎣ ⎣2 ⎣

4

(19) 3251-1012

Resolução Alternativa B Resolução Alternativa A
Considerando que o ponto (0,1) está na circunferência, temos 02 + 12 (I) Verdadeira. Se P pertence simultaneamente à bissetriz dos
– 2.0 – 2.1 + k = 0, logo k = 1. quadrantes ímpares (reta y = x) e à bissetriz dos quadrantes pares
Assim, a circunferência em questão é descrita pela equação: (x – 1)2 + ⎧y = x
(y – 1)2 = 1. (reta y = –x), então ele satisfaz o sistema ⎨ . Logo, P = (0,0).
O ponto P da circunferência mais próximo da origem pode ser obtido ⎩y = − x
geometricamente ao construirmos a reta que passa pela origem (0,0) e Assim, temos o gráfico a seguir: a reta y = k é paralela ao eixo x,
pelo centro (1,1) da circunferência. passando pelo ponto (0,k). Assim, o ponto S, simétrico do ponto P em
y relação a esta reta, é o ponto
S = (0,2k), cuja soma das coordenadas é igual a 2k.
y

S(0,2k)
M
y=k
P N
k

x
A partir do gráfico, temos que a distância da origem ao ponto P é dada P(0,0) x
por 2 − 1 . Como este ponto está na reta x = y, temos que esta
distância é a diagonal de um quadrado. Assim: (II) Falsa. Se y 2 − 3 y ≤ x < 0 ⇒ y 2 − 3 y < 0 .
2− 2 Graficamente, a solução desta inequação em y é:
2 −1= x 2 ⇒ x =
2
⎛2− 2 2− 2⎞
Portanto, o ponto P ⎜
⎜ 2
, ⎟ é o baricentro do triângulo MNQ.
+ +
⎝ 2 ⎟⎠
Podemos obter as coordenadas do ponto Q, a partir das coordenadas
do baricentro:
0
– 3

2 − 2 2 + xQ 2 − 2 1 + yQ 0<y <3
= e =
2 3 2 3 Como y é um número inteiro, os únicos valores possíveis nesse
⎛2−3 2 4−3 2⎞ intervalo são y = 1 ou y = 2.
Assim Q = ⎜ , ⎟. ⎧
⎪ y = 1 ⇒ y − 3 y = 1 − 3 ⋅ 1 = −2
2 2
⎜ 2 2 ⎟ Se ⎨ .
⎝ ⎠
⎪ y = 2 ⇒ y − 3y = 2 − 3 ⋅ 2 = −2
2 2
⎩
O triângulo MNQ tem como vértices os pontos M(0,1), N(2,0) e Nesse caso, y 2 − 3 y ≤ x < 0 ⇒ −2 ≤ x < 0 ⇒ x=–2 ou x=–1
Q(xQ,yQ), cuja área é dada por: Logo, existem quatro pontos P(x,y) que atendem às condições: (–1,1),
0 1 1 (–1,2), (–2,1) e (–2,2).
1 1 (III) Verdadeira. A distância de um ponto P(x,y) até o eixo das
AMNQ = 2 0 1 = xQ + 2y Q − 2 .
2 2 abscissas é |y|, enquanto a distância desse mesmo ponto até o ponto
xQ yQ 1
Q(0,6) é dada por ( x − 0)2 + ( y − 6)2 . Assim, o lugar geométrico em
Substituindo as coordenadas de Q temos: questão é:
1 2 x 2 + y 2 − 12y + 36
1 2−3 2 1 9 2 | y |= x + ( y − 6)2 ⇒ y 2 = ⇒
AMNQ == +4−3 2 −2 = 3− 2 4
2 2 2 2
x2
Aproximando 2 = 1, 4 , temos: 3 y 2 + 12y − 36 − x 2 = 0 ⇒ y 2 + 4 y − = 12
3
1 Completando quadrados nessa equação, temos:
AMNQ= 3 − 6,3 = 1,65 , que está entre 1,5 e 2.
2 x2 ( y + 2)2 x 2
y 2 + 2 ⋅ y ⋅ +22 − = 12 + 22 ⇒ − =1
3 16 48
QUESTÃO 44 Esta é a equação de uma hipérbole centrada no ponto (0,–2), com as
Classifique em (V) verdadeira ou (F) falsa cada afirmativa abaixo medidas a 2 = 16 e b2 = 48 .
sobre o ponto P(x,y) no plano cartesiano. Logo, c 2 = a 2 + b 2 = 16 + 48 = 64 ⇒ c = 8 .
( ) Se o ponto P pertence simultaneamente às bissetrizes dos
c 8
quadrantes ímpares e dos quadrantes pares, então o ponto simétrico A excentricidade da elipse é então dada por: e = = =2
de P em relação à reta y = k (k ∈ *) tem a soma das coordenadas a 4
igual a 2k.
( ) Sendo {x,y} ⊂ , então existem apenas dois pontos P(x,y) que QUESTÃO 45
Considere as curvas, dadas pelas equações
⎧x < 0
⎪ (I) 16x2 + 4y2 + 128x – 24y + 228 = 0
atendem às condições ⎨ 2
⎪y − 3y ≤ x
⎩ (II) y = 7 - |x|
(III) y2 – 6y – x + 5 = 0
( ) Os pontos P(x,y) tais que a sua distância ao eixo das abscissas é
Analise cada afirmação a seguir, classificando-a em VERDADEIRA ou
igual à metade da distância de P ao ponto Q(0,6) formam uma
FALSA
hipérbole de excentricidade igual a 2.
Sobre as afirmativas tem-se
(01) O gráfico de (I) é representado por uma elipse, de (II) por duas
a) apenas uma falsa.
retas e de (III) por uma parábola.
b) apenas duas falsas.
(02) O centro de (I) é um ponto de (II) e coincide com o vértice de (III).
c) todas falsas.
(04) A soma das coordenadas do foco de (III) é um número menor que
d) todas verdadeiras.
-1

5

(19) 3251-1012

π ⎛ 3⎞ 3
(08) A excentricidade de (I) é igual a cos b) Se a função s: D é tal que s( x ) = f ⎜ x + ⎟ , então s(0) = −
6 ⎝ 2⎠ 2
A soma dos itens verdadeiros é um número do intervalo c) O domínio da função r: E tal que r(x)= f(x)-3 é o intervalo real [-6
a)[1,3] b)[4,7] c) [8,11] d) [12,15]
, 6]
Resolução Alternativa C d) A função r: E tal que r(x)= f(x) - 3 NÃO possui raízes em
(01) Falso
( x + 4)2 ( y − 3)2 Resolução Alternativa D
(I) A equação pode ser reescrita como + = 1 , que Analisando cada item:
4 16
a) Correta: O gráfico da função h é o mesmo da função f deslocado
representa uma elipse com eixo maior vertical e centro no ponto C = (- 3/2 no eixo y.
4,3) Analisando os pontos de máximos e mínimos de f, podemos observar
(II) Da definição de módulo, temos: que no intervalo [-3,3/2] a função é descrita por f(x) = - x, o que implica
⎧ y = 7 − x, se x ≥ 0 que seus pontos de máximo e mínimo são respectivamente 3 e -3/2.
⎨ , ou seja, tal equação representa duas semi- Assim, o ponto de máximo da função h é 3 + 3/2 = 9/2 e o ponto de
⎩ y = 7 + x, se x < 0
retas no plano cartesiano e não duas retas. ⎡ 9⎤
mínimo é -3/2 + 3/2 = 0 e portanto a imagem de h é dada por ⎢0, ⎥ .
(III) Essa última equação pode ser reescrita como ⎣ 2⎦
(y-3)2 = x + 4, que é uma parábola com eixo de simetria horizontal e ⎛ 3⎞ ⎛3⎞ 3
vértice no ponto V = (-4,3) b) Correta: s(0) = f ⎜ 0 + ⎟ = f ⎜ ⎟ = −
⎝ 2⎠ ⎝2⎠ 2
(02) Verdadeiro
Do item anterior, vemos que P=(-4,3) é o centro da elipse e o vértice c) O domínio de r é o mesmo domínio de f. Determinando os valores
da parábola. Além disso, P pertence ao gráfico de (II) pois x = -4 ⇒ y de a:
= 7-|-4| = 3 Temos que o coeficiente angular no intervalo [-a,-3] é dado por
(04) Falso ⎛ 3⎞
0 − ⎜− ⎟
1 3−0 ⎝ 2⎠ ⇒ a −5 = 3 ⋅ 2 ⇒ a = 6 .
(y – 3)2 = x + 4 ⇒ p = , onde p é o parâmetro da parábola (distância =
2 ( −3 ) − ( −5 ) ( −5 ) − ( −a ) 2 3
do foco a reta diretriz). Portanto, o domínio de f e de r é dado pelo intervalo real:
Sendo o vértice da parábola o ponto V = (-4,3) e dado que seu eixo de [-a , a] = [-6 , 6]
simetria é horizontal obtemos o foco F por: d) Incorreta: a função r: E tal que r(x)= f(x) - 3 apresentará raiz real
p 7 para x=-3.
F = (−4 + ,3) = (− ,3)
2 2 Do enunciado f(-3)=3 ⇒ r(-3) = f(-3)-3= 3-3=0
1 Logo -3 é raiz da função r.
Logo xf + yf = -
2
(08) Verdadeiro
( x + 4)2 ( y − 3)2
Na equação da elipse + = 1 , o primeiro denominado
4 16
representa o valor de a2 (onde a é o semi-eixo maior da elipse) e o
segundo denominador representa o valor de b2 (onde b é o semi-eixo
menor da elipse). Assim: a = 4 e b = 2
Da relação fundamental da elipse a 2 = b 2 + c 2 (onde c é a metade da
distância focal), temos:
c= 2 3
c
Logo a excentricidade, definida como e = vale
a
3 π
= cos
2 6
Portanto, soma 02+08=10.
QUESTÃO 47
QUESTÃO 46 Considere todo x ∈ que torne possível e verdadeira a igualdade
Na figura abaixo, está representado o gráfico da função real f:[- log[f ( x − 1)] = log x − 2 x 2 + 1 , onde f é uma função real de A em B
2 4

a,a] , onde f(0)=0. e marque a alternativa correta.
a) O conjunto imagem de f é Im = + − {1}
b) f é uma função injetora.
c) Se B = + − {1} , então existe a inversa de f .
d) f tem domínio A = { x ∈ / | x |> 1}
Observe que x 4 − 2 x 2 + 1 = ( x 2 − 1)2 =| x 2 − 1| , e portanto,
log x 4 − 2 x 2 + 1 = log | x 2 − 1|
Pelas condições de existência do logaritmo, o logaritmando deve ser
positivo, portanto devemos ter
Analise as alternativas abaixo e marque a INCORRETA. i) | x 2 − 1|> 0 (o que acontece se e somente se x ≠ ±1 )
3 ii) f ( x 2 − 1) > 0 .
a) O conjunto imagem da função h: A B, definida por h ( x ) = f ( x ) +
2 Nos pontos onde isso acontece, vale:
⎡ 9⎤ log[f ( x 2 − 1)] = log | x 2 − 1|⇒ f ( x 2 − 1) =| x 2 − 1| .
é Im = ⎢0, ⎥
⎣ 2⎦ Assim, temos que f (w ) =| w |

6

(19) 3251-1012

Verificando a segunda condição de existência citada, note que, (gogof-1) (5/2) = g(g(f–1(5/2)))=g(g(1))=g(0)=4>0.
f (w ) =| w | , que é sempre não negativa. c) Incorreta:
Esta função se anula somente quando w = 0 ou seja
Estudando os sinais da expressão
[f ( x )]2 temos:
f ( x 2 − 1) = 0 ⇔ x 2 − 1 = 0 ⇔ x = ±1 g( x )
Logo o domínio da função f é − {1, −1} ⎧ 2
⎪[f ( x )] > 0 ⇔ x ≠ − 3 ⎧g ( x ) > 0 ⇔ 1 < x < 4
2
Assim, o gráfico da função f deve ser: ⎪ ⎪
⎨ e ⎨g ( x ) = 0 ⇔ x = 1 ou x = 4
y ⎪[f ( x )]2 = 0 ⇔ x = − 2 ⎪g ( x ) < 0 ⇔ x < 1 ou x > 4
⎪
⎩ 3 ⎩
A expressão não é definida para x=1 ou x=4. Assim:
⎧ [f ( x )]2 2
⎪ =0⇔ x=−
⎪ g( x ) 3
⎨
⎪ [f ( x )]
2
1 2
> 0 ⇔ x < 1 e x ≠ − ou x > 4
⎪
⎩ g( x ) 3
13 1
–1 1 x d) Incorreta: f(x) – g(x) = − x 2 + x − 3 , cujas raízes são e6eé
2 2
1
não positiva para x ≤ ou x ≥ 6 .
a) Verdadeira: conforme o gráfico, todos os pontos não-negativos do 2
eixo y, exceto o 1, foram atingidos, e portanto Im(f ) = + − {1} .
b) Falsa: por exemplo, temos f ( −2) = f (2) = 2 . QUESTÃO 49
c) Falsa: se fixarmos o contradomínio da função f como sendo Considere as funções reais
B = + − {1} , apenas a tornaremos uma função sobrejetora, mas ela f : R+ * → R tal que f ( x ) = x − 2
x
continuará sendo não injetora. Se não é uma função injetora, com ⎛ 1⎞
mais razão não é bijetora e, portanto, não admite inversa. g : R → R+ * tal que g ( x ) = ⎜ ⎟
⎝2⎠
d) Falsa: conforme demonstrado no início, o domínio da função é
− {1, −1} . h : R+ * → R tal que h( x ) = − log2 x

e marque a alternativa correta.
QUESTÃO 48 g( x )
As funções f: do 1º grau e g: [b, +∞[ do 2º grau estão a) O domínio da função k definida por k ( x ) = é o conjunto dos
h( x )
representadas no gráfico abaixo. números reais positivos.
f ( x ) ⋅ h −1( x )
b) A função j definida por j ( x ) = se anula em dois pontos
(g f )( x )
distintos.
c) A função m definida por m( x ) = −1 + (g f )( x ) não possui raiz.
d) Se g(h(a)) = 8 e h(g (2b )) = log3 9 , então (a − b ) é um número
primo.

Resolução Alternativa D
a) Falsa, pois para x = 1 , temos h(1) = 0 , e portanto a função
g( x )
k( x ) = não está definida para x = 1. O domínio da função k seria
h( x )
R+ * − {1}
Com base nas informações acima é correto afirmar que:
a) o menor valor de b que torna a função g sobrejetora é um número b) Falsa.
inteiro. Temos h(w ) = − log2 w e chamando h(w ) = x , temos:
b) (gogof-1) (5/2) > 0
h −1( x ) = w . Assim, x = − log2 w = − log2 h −1( x ) ⇒
[f ( x )]
2

c) > 0 ⇔ {x ∈ | x < 1 ou x > 4} ⎛ 1⎞
x

g( x ) log2 h −1( x ) = − x ⇒ h −1( x ) = 2− x = ⎜ ⎟ = g ( x ) .
⎝2⎠
d) f(x)-g(x)≤0 ⇔ { x ∈ | x ≤ 0 ou x ≥ 6}
f (x) x −2
⎛ 1⎞ ⎛ 1⎞
Resolução Alternativa B Por outro lado, (g f )( x ) = g (f ( x )) = ⎜ ⎟ =⎜ ⎟ .
Da observação do gráfico, é possível descobrir que: ⎝2⎠ ⎝2⎠
x
3 ⎛ 1⎞
f (x) =
x +1 ( x − 2) ⋅ ⎜ ⎟
2 f ( x ) ⋅ h −1( x ) ⎝ 2 ⎠ = ( x − 2) , de modo que a
Logo, j ( x ) = = x −2
Assim, x= -2/3 será raiz desta função. (g f )( x ) ⎛ 1⎞ 4
⎜ ⎟
g( x ) = x 2 − 5 x + 4 ⎝2⎠
Assim, x=1 e x=4 serão raízes da função g, e seu ponto de mínimo função j se anula apenas num ponto, quando x=2
Δ 9 ⎛ 1⎞
x −2
será y v = − =− . c) Falsa. Pelo item anterior, (g f )( x ) = ⎜ ⎟ , e assim, temos
4a 4 ⎝2⎠
⎧ 9⎫ x −2
a) Incorreta, pois a imagem de g(x)= ⎨ y ∈ R | y ≥ − ⎬ . Logo, para que ⎛ 1⎞
⎩ 4⎭ m( x ) = −1 + (g f )( x ) = ⎜ ⎟ − 1 .
⎝2⎠
g(x) seja sobrejetora, o valor mínimo de b é – 9/4, que é racional.
b) Correta, pois observando o gráfico, temos que, da função inversa, Resolvendo a equação m( x ) = 0 , temos
f(1)=5/2 ⇔ f–1(5/2) =1. Ainda observando o gráfico, temos:
7

(19) 3251-1012

⎛ 1⎞
x −2
⎛ 1⎞
x −2 educação, R$5.000,00 com o total pago à Previdência, e R$1.500,00
⎜ 2 ⎟ − 1 = 0 ⇒ ⎜ 2 ⎟ = 1⇒ x = 2 por dependente.
⎝ ⎠ ⎝ ⎠ Nessas condições, sabendo-se que o valor do imposto pago por este
Assim, a função m possui uma raiz. trabalhador, no ano de 2007, foi de R$3.515,00, o número de
d) Verdadeira. Observe que g h( x ) = x para todo x ∈ R+ * e dependentes considerado foi:
a) 2 b) 3 c) 4 d) 6
h g(w ) = w para todo w ∈ R , já que as funções g e h são funções
inversas uma da outra. Logo: Resolução Alternativa C
Seja x o total de dependentes. As deduções do imposto de renda
⎧8 = g (h(a )) = a ⇒ a = 8
⎨ desse trabalhador somam um total de:
⎩2 = log3 9 = h( g (2b )) = 2b ⇒ b = 1 R$9400,00 + x.R$1500,00
Portanto: a − b = 8 − 1 = 7 , que é um número primo. O valor limite máximo (não incluído) de alguém que paga imposto com
uma alíquota de 15% é calculado por:
15%. ( 30000 ) − 2250 = 2250
QUESTÃO 50
"A Arrecadação da CPMF, devido à ampliação de sua abrangência, e Assim, analisemos o imposto pago, utilizando a alíquota de 27,5%:
ao aumento da alíquota, cresceu mais de 140% nos últimos anos (em I=27,5%. ⎡50000-(9400+1500x)⎤ -6000=3515
⎣ ⎦
bilhões de reais por ano)".
9515
Revista Veja - 14/03/2007 40600 − 1500x = = 34600 ⇒ 1500x = 6000
0,275
6000
⇒x= =4
1500
Logo, o total de dependentes é 4.

QUESTÃO 52
Sabendo-se que b é um número real tal que b > 1 e que a função real
−x
f: B é tal que f(x) = 2 − b , analise as alternativas abaixo e
marque a FALSA.
a) A função f admite valor mínimo.
1
b) x ≤ - 1 ⇔ 2 - ≤ f(x) < 2
b
c) A função f é par.
d) Se B = [0, 2[ então f é sobrejetora.
Seja f(x) = 2 − b−|x| . Assim, f(−x) = 2 − b|− x| = 2 − b|x| = f(x) , e a
função f é par. Logo, a alternativa (c) está correta.
Supondo que o crescimento da arrecadação representado no gráfico Como b > 1, podemos reescrever a função como
acima é linear do ano 2005 ao ano de 2007 e que y% representa o 1 1
aumento da arrecadação do ano de 2005 ao ano de 2006, é correto f(x) = 2 − b−|x| = 2 − , onde 0 < |x| ≤ 1 .
b|x| b
afirmar que y é um número do intervalo:
a) [8, 9[ b) [9, 10[ c) [10, 11[ d) [11, 12[ Daqui, segue que 1 ≤ f(x) ≤ 2 , de modo que f(x) admite um mínimo
e um máximo. Além disso, fica evidente que o conjunto-imagem de f é
Resolução Alternativa B o intervalo [1;2], de modo que a alternativa (a) está correta, enquanto
De acordo com o gráfico, de 2005 a 2007, a arrecadação da CPMF a alternativa (d) está incorreta.
salta de R$29,2 bilhões de reais para um valor estimado de R$34,8 Para verificar a validade da alternativa (b), note que se
bilhões.
1 1 1 1 1
Supondo linear o gráfico entre os anos citados, temos que a x ≤ −1 ⇒ |x| ≤ ⇒ − |x| ≥ − ⇒ f(x) ≥ 2 −
29,2 + 34,8 b b b b b
arrecadação em 2006 é dada por =32 bilhões. 1
2 Temos também que lim = 2 e portanto 2 − ≤ f(x) ≤ 2
O aumento de arrecadação, tomando com base o ano de 2005, x →−∞ b
R $32bi
corresponde a: ≈ 1,09 . Desta forma a arrecadação
R $29,2bi QUESTÃO 53
aumentou cerca de 9% de 2005 para 2006. Sabendo-se que a função real f: D → B definida por
Portanto y pertence ao intervalo [9, 10[ x
f(x) = é inversível e que D e B são conjuntos os mais amplos
1− x
QUESTÃO 51 possíveis, é FALSO afirmar que
Considere a tabela para cálculo do imposto de renda a ser pago à a) f é crescente para todo x tal que x < 1 ou x > 1.
Receita federal no ano de 2007 – ano base 2006 (valores b) a equação da assíntota horizontal de f é y = -1.
arredondados para facilitar os cálculos). c) se g é tal que g(x) = |f-1(x)|, então não existe x real tal que g(x) = 1
Rendimento para base Alíquota Parcela a deduzir d) f-1(0) + f-1(-½) < 0
de cálculo (R$) (%) (R$)
até 14.999,99 Isento -
Resolução Alternativa C
a) Correta.
De 15.000,00 a 30.000,00 15 2.250,00 Tome x,y ≠ 1, e suponha que f(x) > f(y):
acima de 30.000,00 27,5 6.000,00
x y x y x(1 − y) − y(1 − x)
Para se conhecer o rendimento para base de cálculo, deve-se subtrair > ⇒ − >0⇒ >0
do rendimento bruto todas as deduções a que se tem direito. Esse 1−x 1−y 1−x 1− y (1 − x)(1 − y)
rendimento para base de cálculo é multiplicado pela alíquota x−y
correspondente. Em seguida, subtrai-se a parcela a deduzir ⇒ >0
(1 − x)(1 − y)
correspondente, de acordo com a tabela acima, obtendo-se assim o
valor do imposto de renda a ser pago. Se x,y < 1, temos que (1-x)(1-y) > 0. Da mesma forma, se x,y > 1,
Um trabalhador, cujo rendimento bruto foi de R$50.000,00 teve direito também encontramos (1-x)(1-y) > 0. Em ambos os casos temos x – y
às seguintes deduções: R$4.400,00 com o total de gastos em > 0 e, conseqüentemente,
x > y. Assim, pela hipótese de que f(x) > f(y), f é crescente para todo x
8

(19) 3251-1012

> 1 ou x < 1. Observe que esse resultado só é válido nesse caso,
a 6
quando olhamos o domínio de maneira separada. Caso contrário, f Por Pitágoras EP = .
não seria crescente. Assim, a alternativa (a) está correta. 2
b) Correta. 3 6
x x −1 1 1 Assim cos θ = ; senθ = e tgθ = 2 .
Reescrevendo f(x) = = + = −1, 3 3
1−x 1− x 1−x 1− x
percebemos que o gráfico de nossa função corresponde à uma Observando tg θ, como 1 < 2 < 3 , temos 45° < θ < 60° ;
hipérbole de assíntota vertical x = 1. Fazendo x → ±∞ , notamos que
1 (01) VERDADEIRA: se 45° < θ < 60° ⇒ 90o < θ < 120o;
− 1 → −1 , de modo que y = -1 é a assíntota horizontal de
1−x (02) VERDADEIRA: tgθ = 2 , e como 1 < 2 < 3 , então
nossa função, o que torna a alternativa (b) correta. 45° < θ < 60° ;
c) Incorreta.
2.tgθ 2 2
Note que se g(x) =| f −1(x) | , existe algum ponto x tal que (04) VERDADEIRA: tg (2θ ) = = = −2 2 = −2tgθ ;
1 − tg 2θ 1 − 2
f −1(x) = −1 , uma vez que −1 ∈ D . Assim, existe x tal que 6 3 2 2 tg 2θ 2 2
−1 (08) FALSA: sen(2θ ) = 2.senθ .cosθ = 2. . = ≠ =−
g(x) =| f (x) |=| −1 |= 1 , e a alternativa (c) está incorreta. 3 3 3 3 3
d) Correta. (16) FALSA:
Seja a função inversa de f dada por −1
f (x) = y , assim, ⎛ 3π ⎞ 1 1 1
cossec ⎜ −θ ⎟ = = = = − 3 ≠ tg 60°
y x ⎝ 2 ⎠ sen ⎛ 3π ⎞ −senθ 3
x= ⇒ y = x(1 − y) = x − xy ⇒ y = f −1(x) = . Desse ⎜ −θ ⎟ −
1−y 1+ x ⎝ 2 ⎠ 3
Soma das proposições verdadeiras: 01 + 02 + 04 = 07
−1
⎛ 1⎞ 2 = −1 <0, e a
modo, temos que f −1(0) + f −1 ⎜ − ⎟ = 0 +
⎝ 2⎠ 1
2
QUESTÃO 55
Considerando as definições e propriedades das funções
alternativa (d) está correta.
trigonométricas, marque a alternativa correta.
a) A função f definida por f ( x ) = sen2 x − cos2 x possui período e
QUESTÃO 54
No cubo da figura abaixo, considere P o ponto de encontro das imagem, respectivamente, iguais a π e ⎡0, 2 ⎤ .
⎣ ⎦
diagonais da face ABCD e Q o ponto de encontro das diagonais da
face EFGH e θ é medida do ângulo PÊQ. b) Se f e g são funções tais que f ( x ) = tgx e g ( x ) = x , sabendo-se
que existe a função j definida por j ( x ) = (fog )( x ) , então j é periódica.
⎤π π ⎡
c) No intervalo de ⎥ , ⎢ a função h definida por h( x ) = cos 2 x é
⎦4 2⎣
decrescente.
3x − 1
d) O domínio da função g definida por g ( x ) = 3.arcsen é
2
⎡1 ⎤
D = ⎢ ,1⎥
⎣3 ⎦
Analise as proposições seguintes. a) Incorreta. Vamos transformar a diferença sen2x – cos2x numa
(01) 2θ é um ângulo maior que 90º única função trigonométrica:
(02) θ é um ângulo do intervalo [45º, 60º] sen 2 x − cos 2 x = 1 ⋅ sen 2 x − 1 ⋅ cos 2 x =
(04) tg 2θ = -2tg θ 1 1
1 12 + 12 ( ⋅ sen 2 x − ⋅ cos 2 x) =
(08) sen 2θ = tg2θ 2 2
3 1 +1 1 + 12
2

⎛ 3π ⎞ 2 2 π π
(16) cossec ⎜ − θ ⎟ = tg60º 2( sen2 x − cos 2 x) = 2 (cos sen2 x − sen cos 2 x) =
⎝ 2 ⎠ 2 2 4 4
O número que representa a soma das proposições verdadeiras é ⎛ π⎞ ⎛ π⎞
múltiplo de: 2 ⋅ sen⎜ 2 x − ⎟ . Logo, f ( x) = 2 ⋅ sen⎜ 2 x − ⎟
⎝ 4⎠ ⎝ 4⎠
a) 2 b) 3 c) 5 d) 7
Resolução Alternativa D ⎛ π⎞ ⎛ π⎞
Como − 1 ≤ sen⎜ 2 x − ⎟ ≤ 1 ⇒ 0 ≤ sen⎜ 2 x − ⎟ ≤ 1 ⇒
Do enunciado,podemos formar o triângulo PEQ a seguir: ⎝ 4⎠ ⎝ 4⎠
⎛ π⎞
0 ≤ 2 sen⎜ 2 x − ⎟ ≤ 2 ⇒ 0 ≤ f ( x) ≤ 2 ⇒ Im( f ) = [0, 2 ]
⎝ 4⎠
O gráfico da função f é:

a 2
Do triângulo PEQ, temos: EQ = ; PQ = a
2

9

Mat exercicios resolvidos

Recomendados

Recomendados

Mais conteúdo relacionado

Mais procurados

Mais procurados (20)

Destaque

Destaque (20)

Semelhante a Mat exercicios resolvidos

Semelhante a Mat exercicios resolvidos (20)

Mais de comentada

Mais de comentada (20)

Último

Último (20)

Mat exercicios resolvidos