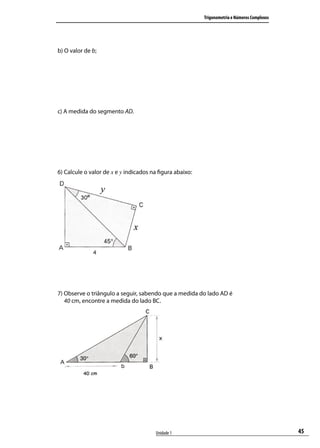
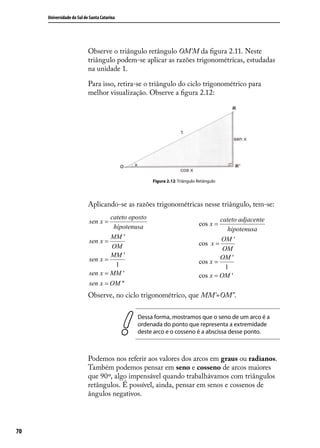
Este documento fornece informações sobre o curso de Trigonometria e Números Complexos oferecido pela Universidade do Sul de Santa Catarina (Unisul). Ele apresenta os créditos do curso, a ementa, os objetivos gerais e específicos, a carga horária e a equipe responsável pelo curso.


































![Trigonometria e Números Complexos
Existem três casos a considerar:
O triângulo ABC é retângulo;
O triângulo ABC é obtusângulo;
O triângulo ABC é acutângulo.
Faremos a demonstração quando o triângulo for acutângulo. Os
outros dois casos você irá demonstrar na resolução do exercício 19
das atividades de auto-avaliação ao final desta unidade.
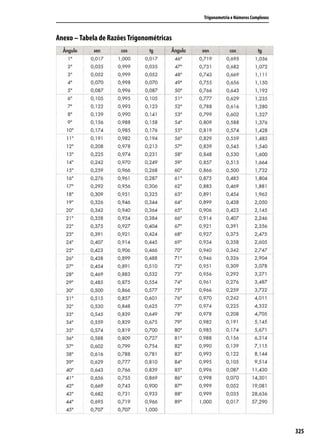
Considere o triângulo ABC acutângulo, representado na figura
1.15:
Figura 1.15: Representação do triângulo para demonstração
Sejam AH1 e BH2 as alturas relativas aos lados BC e AC
respectivamente.
No triângulo retângulo AH1C, temos que
^ h1 ^
sen C = ⇒ h1 = b.sen C . [1]
b
No triângulo retângulo AH1B, temos que
^ h1 ^
sen B = ⇒ h1 = c.sen B . [2]
c
Comparando [1] e [2], temos:
^ ^ b c
b.sen C = c.sen B ⇒ ^
= ^ [A]
sen B sen C
Unidade 1 37](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-37-320.jpg)
![Universidade do Sul de Santa Catarina
No triângulo retângulo BH2C, temos que
^ h2 ^
sen C = ⇒ h2 = a.sen C . [3]
a
No triângulo retângulo AH2B, temos que
^ h2 ^
sen A = ⇒ h2 = c.sen A . [4]
c
Comparando [3] e [4], temos:
^ ^ a c
a.sen C = c.sen A ⇒ ^
= ^ [B]
sen A sen C
De [A] e [B] podemos concluir que:
a b c
^
= ^
= ^
sen A sen B sen C
Lei dos cossenos
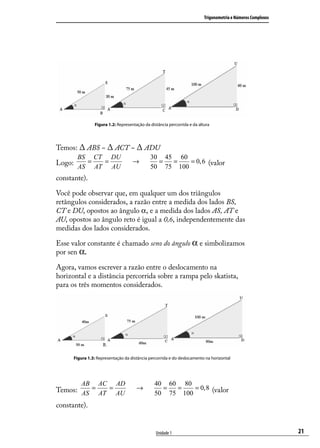
Na duplicação da BR-101, em um dos pontos do trecho sul, é
necessário a construção de uma ponte que una os pontos A e
B conforme a figura a seguir. O engenheiro responsável pela
obra só conseguiu as seguintes medidas: AC=30m, BC=50m e a
medida do ângulo entre esses lados 120º. Ele necessita descobrir
qual a extensão da ponte.
Modelo real Modelo matemático
Figura 1.16: Modelo real e matemático do problema enunciado no exemplo.
38](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-38-320.jpg)


![Trigonometria e Números Complexos
Figura 1.19: Representação dos triângulos para demonstração.
Aplicando o Teorema de Pitágoras em ambos os triângulos,
temos:
b2 = m2 + h2 a 2 = h2 +(c-m)2
h2 = b2 - m2 [1] a 2 = h2 + c2 -2.c.m + m2 [2]
Substituindo [1] em [2], temos:
a 2 = b2 - m2 + c2 -2.c.m + m2
a 2 = b2 + c2 -2.c.m [3]
^ ^ m
Note no triângulo A H C que temos: cos A =
b
Logo m = b.cos [4]
Substituindo [4] em [3], temos:
a 2 = b2 + c2 -2.b.c. cosÂ
De forma análoga, você demonstra que:
^
b2 = a 2 + c2 -2.a.c. cos B .
^
c2 = a 2 + b2 -2.a.b. cos C .
Unidade 1 41](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-41-320.jpg)



















































![Trigonometria e Números Complexos
Você sabia...
Na natureza encontra-se uma série de fenômenos ditos
periódicos, ou seja, que se repetem sem alteração cada vez
que transcorre um intervalo de tempo determinado.
Como exemplo de fenômenos periódicos, é possível citar as
ondas do mar, sonoras, ou mesmo ondas eletromagnéticas.
Função Seno
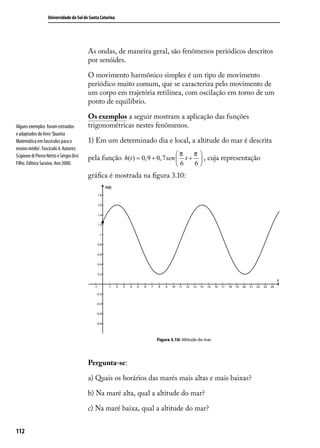
Observe a figura 3.1:
Figura 3.1: Função Seno
A função seno é uma função f: IR → IR que, a todo arco de
medida x∈IR, associa a ordenada y do ponto P.
f(x) = senx
O domínio da função seno é D(f)=IR
A imagem da função seno, Im (f), é o intervalo [-1,1].
Unidade 3 97](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-97-320.jpg)
![Universidade do Sul de Santa Catarina
Função Cosseno
Observe a figura 3.2:
Figura 3.2: Função Cosseno
A função cosseno é uma função f: IR → IR que a todo arco
de medida x∈IR associa a abscissa x do ponto P.
f(x) = cos x
O domínio da função cosseno é D(f)=IR.
A imagem da função cosseno, Im (f), é o intervalo [-1,1].
Gráfico da Função Seno: Senóide
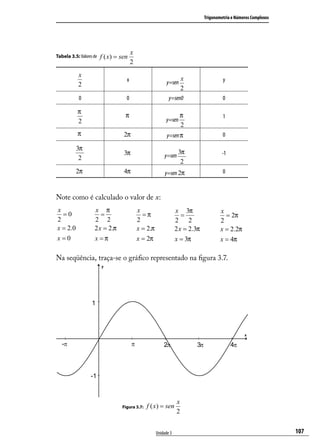
Seja f(x) = sen x
Inicialmente, constrói-se a tabela com x variando [-2π, 2π].
Tabela 3.1: Valores do seno
3π π π 3π
x -2π − -π − 0 π 2π
2 2 2 2
sen x 0 1 0 -1 0 1 0 -1 0
98](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-98-320.jpg)
![Trigonometria e Números Complexos
Observe o gráfico na figura 3.3:
Figura 3.3: f(x) = senx
Observando o gráfico da função f(x)=sen x, no intervalo
[-2 π ,2 π ], tem-se que:
A função é periódica de período 2 π , pois a função repete
os seus valores nos intervalos [-2 π ,0] e [0,2 π ], ou seja,
toda vez que somamos 2 π a um determinado valor de x,
a função seno assume o mesmo valor.
O estudo da variação nos mostra que f(x)=sen x tem um
valor mínimo -1, um valor máximo 1 e assume todos os
valores reais entre -1 e 1, logo, a imagem da função é o
intervalo Im=[-1,1].
O domínio da função f(x)=sen x é D= [-2 π ,2 π ].
Nos intervalos ]−2π , −π [ e ]0; π [ , a função f(x)=sen x
assume valores positivos.
Unidade 3 99](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-99-320.jpg)
![Universidade do Sul de Santa Catarina
Nos intervalos ]−π , 0[ e ]π ; 2π [ , a função f(x)=sen x
assume valores negativos.
A função f(x)=sen x é crescente nos intervalos
−3π π π 3π
−2π ; 2 , − 2 , 2 e 2 ; 2π .
A função f(x)=sen x é decrescente nos intervalos
−3π −π π 3π
2 ; e ; .
2
2 2
A função f(x)=sen x é ímpar pois f(x) = -f(-x).
A função f(x)=sen x possui valor máximo quando
−3π rad e x = π rad.
x=
2 2
−π
A função f(x)=sen x possui valor mínimo quando x =
2
3π
rad e x = rad.
2
Generalizando algumas características da função f(x)= sen x
tem-se:
O domínio da função é D(f)=IR, pois é possível
estender a senóide ao longo do eixo x.
O conjunto imagem da função é Im(f)=[-1,1].
A função f(x)= sen x possui valor máximo para
π
x ∈ IR | x = + 2kπ , k ∈ Z .
2
A função f(x)= sen x possui valor mínimo para
3π
x ∈ IR | x = + 2 kπ , k ∈ Z .
2
100](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-100-320.jpg)
![Trigonometria e Números Complexos
Você lembra?
Você já estudou na disciplina ‘Tópicos da Matemática
Elementar I’ cada uma das características das funções
y=sen x e y=cos x, citadas. Assim, você deve lembrar das
definições formais de função periódica, função par e ímpar.
Então:
Função Periódica: Dizemos que uma função é periódica se
existe um número real T diferente de zero, tal que f(x+T)=f(x)
para todo
x ∈D(f).
Função Par e Ímpar: Uma função f(x) é par, se para todo x no
seu domínio temos f(x)=f(-x).
Uma função é ímpar se, para todo x no seu domínio temos
f(x)=-f(-x).
Gráfico da Função Cosseno: Cossenóide
Seja f(x) = cos x
Inicialmente, constrói-se a tabela com x variando [-2π, 2π].
Tabela 3.2: Valores do cosseno
3π π π 3π
x -2π − -π − 0 π 2π
2 2 2 2
cos x 1 0 -1 0 1 0 -1 0 1
Unidade 3 101](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-101-320.jpg)
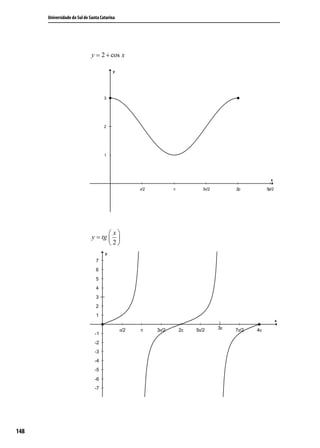
![Universidade do Sul de Santa Catarina
Agora observe o gráfico na figura 3.4:
Figura 3.4: f(x) = cos x
Observando o gráfico da função f(x)=cos x, no intervalo
[-2 π ,2 π ], tem-se que:
A função é periódica de período 2 π , pois a função repete
os seus valores nos intervalos [-2 π ,0] e [0,2 π ], ou seja,
toda vez que somamos 2 π a um determinado valor de x,
a função cosseno assume o mesmo valor.
O estudo da variação nos mostra que f(x)=cos x tem um
valor mínimo -1, um valor máximo 1 e assume todos os
valores reais entre -1 e 1, logo, a imagem da função é o
intervalo Im=[-1,1].
O domínio da função f(x)=cos x é D= [-2 π ,2 π ].
3π π π 3π
Nos intervalos −2π , − , − , e ; 2π a
2 2 2
2
função f(x)=cos x assume valores positivos.
3π π π 3π
Nos intervalos − ,− e ; , a função
2 2 2 2
f(x)=cosx assume valores negativos.
102](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-102-320.jpg)
![Trigonometria e Números Complexos
A função f(x)=cos x é crescente nos intervalos [−π ;0] e
[π , 2π ].
A função f(x)=cos x é decrescente nos intervalos
[−2π ; −π ] e [0;π ].
A função f(x)=cos x é par, pois, f(x) = f(-x).
A função f(x)=cos x possui valor máximo quando
x = 0 rad .
A função f(x)=cos x possui valor mínimo quando x = −π
rad e x = π rad.
Generalizando algumas características da função f(x)= cos x
tem-se:
O domínio da função é D(f)=IR, pois é possível estender
a cossenóide ao longo do eixo x.
O conjunto imagem da função é Im(f)=[-1,1].
A função f(x)= cos x possui valor máximo para
{x ∈ IR | x = 2kπ , k ∈ Z }.
A função f(x)= cos x possui valor mínimo para
{x ∈ IR | x = π + 2kπ , k ∈ Z }.
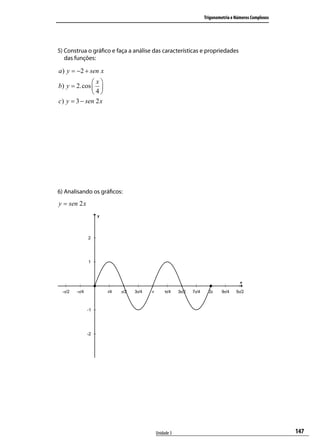
1) Construa e analise os gráficos das funções a seguir,
determinando o domínio, a imagem e o período.
a ) f ( x) = 2 + sen x
b) f ( x) = sen x − 1
a) Solução:
Inicialmente, constrói-se a tabela 3.3 para a elaboração do
gráfico:
Unidade 3 103](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-103-320.jpg)
![Universidade do Sul de Santa Catarina
Tabela 3.3: Valores de f(x)=2+sen x
x sen x y=2+sen x y
0 sen0=0 y=2+0 2
π sen
π =1
y=2+1 3
2 2
π sen π =0 y=2+0 2
3π sen 3π =-1 y=2+(-1) 1
2 2
2π sen 2π =0 y=2+0 2
Na seqüência, traça-se o gráfico no plano cartesiano representado
na figura 3.5.
Figura 3.5: f(x) = 2 + sen x
D=IR;
Im=[1,3];
P=2 π .
b) Solução:
Constrói-se a tabela 3.4 para a elaboração do gráfico:
104](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-104-320.jpg)
![Trigonometria e Números Complexos
Tabela 3.4: Valores de f(x)=sen x -1
x senx y=senx - 1 y
0 sen0=0 y=0-1 -1
π π
sen =1 y=1-1 0
2 2
π sen π =0 y=0-1 -1
3π sen
3π =-1
y=-1-1 -2
2 2
2π sen 2π =0 y=0-1 -1
Na seqüência, traça-se o gráfico no plano cartesiano representado
na figura 3.6.
Figura 3.6: f(x) = sen x -1
D=IR;
Im=[-2,0];
P=2 π .
Unidade 3 105](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-105-320.jpg)
![Universidade do Sul de Santa Catarina
Comparando os gráficos dos itens a e b com o gráfico da figura
3.3 no intervalo [0, 2 π ], você poderá observar que
f(x)=2+sen x pode ser obtida transladando-se o gráfico de y=sen x
em duas unidades no sentido positivo de Oy.
Quando se compara o gráfico de f(x) = sen x-1, observa-se que ele
pode ser obtido fazendo a translação de uma unidade do gráfico
f(x)=sen x, no sentido negativo de Oy.
x
2) Construa o gráfico da função f(x)=sen , dê o domínio, a
2
imagem e o período.
Você sabia...
Multiplicando o valor de x da função y=senx por um número
real, vamos observar que o período da função fica 2 π
dividido por este número. Por exemplo, y=sen(kx) o período
é P= .
Solução:
Inicialmente, constrói-se a tabela 3.5 para a elaboração do
gráfico. Para isso, calcula-se o período desta função, pois se nota
que o mesmo será diferente de 2 π .
Observe: P=
Como k = 1 , temos:
2
P=
Como o seno é uma função periódica de período 2 π , basta variar
o argumento x num intervalo de amplitude 2 π . Atribuindo
2
x
a valores adequados e pertencentes ao intervalo [0, 2π ] e
2
calculando x e y, temos:
106](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-106-320.jpg)

![Trigonometria e Números Complexos
Na seqüência, traça-se o gráfico no plano cartesiano,
representado na figura 3.8.
Figura 3.8: f(x) = cos 2x
D = IR;
Im = [-1,1];
P = π.
b) Solução:
Inicialmente, constrói-se a tabela 3.7 para a elaboração do
gráfico.
Calculando o período da função y= cos4x, tem-se:
Nesta função k=4, logo:
2π 2π π
P= = = .
4 4 2
Unidade 3 109](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-109-320.jpg)
![Universidade do Sul de Santa Catarina
Tabela 3.7: Valores de f(x) = cos 4x
4x x y=cos4x y
0 0 y=cos0 1
π π π
y=cos 0
2 8 2
π
π y=cos π -1
4
3π 3π 3π 0
2 8 y=cos
2
π
2π y=cos 2π 1
2
Na seqüência, traça-se o gráfico no plano cartesiano representado
na figura 3.9.
Figura 3.9: f(x) = cos 4x
D = IR;
Im = [-1,1];
π
P= .
2
110](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-110-320.jpg)





![Trigonometria e Números Complexos
Observando as representações geométricas, constrói-se a tabela
3.8 com os valores notáveis da tangente.
Tabela 3.8 Valores Notáveis da Tangente
π π π π 3π
x 0 π 2π
6 4 3 2 2
3 Não Não
tgx 0 1 3 existe 0 existe 0
3
Gráfico da Função Tangente: Tangentóide
Seja f(x) = tg x
Inicialmente, constrói-se a tabela 3.9 com x variando [-2π, 2π].
Tabela 3.9: Valores da tangente
3π π π 3π
x -2π − -π − 0 π 2π
2 2 2 2
Não Não Não Não 0
tg x 0 0 0 0
existe existe existe existe
Figura 3.16: f(x)=tg x
Unidade 3 119](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-119-320.jpg)
![Universidade do Sul de Santa Catarina
Observando o gráfico da função f(x)=tg x, no intervalo
[-2 π ,2 π ], representada na figura 3.16, tem-se que:
A função é periódica de período π , pois a função repete os seus
valores nos intervalos [0, π ] e [ π ,2 π ], ou seja, toda vez que
somarmos π a um determinado valor de x, a função tangente
assume o mesmo valor.
Quando x tende aos valores em que a tg x não existe, o gráfico
da tangente tende ao infinito positivo ou negativo.
O estudo da variação nos mostra que, no intervalo
[-2 π ,2 π ], f(x)=tg x é sempre crescente.
O domínio da função f(x)=tg x é:
3π 3π π π π π 3π 3π
D( f ) = −2π , − ∪ − , − ∪ − , ∪ , ∪ , 2π
2 2 2 2 2 2 2 2
A imagem da função f(x)=tg x é Im(f)=IR.
3π π π 3π
Nos intervalos −2π , − , −π , − 2 , 0, 2 e π , 2 , a
2
função f(x)=tg x assume valores positivos.
3π π π 3π
No intervalo − , −π , − , 0 , , π e , 2π , a
2 2 2 2
função f(x)=tg x assume valores negativos.
A função f(x)=tg x é ímpar, pois tg x=-tg (-x.)
Generalizando, tem-se:
O domínio da função f(x)=tgx é
π
D( f ) = x ∈ IR|x ≠ + kπ , k ∈ Z .
2
A imagem da função f(x)=tg x é Im(f)=IR.
120](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-120-320.jpg)



![Universidade do Sul de Santa Catarina
Gráfico da Função Cotangente
Seja f(x) = cotg x
Inicialmente, constrói-se a tabela 3.10, usando a relação
cos x
cot g x = , ( sen x ≠ 0) , com x variando [-2π, 2π].
sen x
Tabela 3.10: Valores da cotangente
3π π π 3π
x -2π − -π − 0 π 2π
2 2 2 2
Não Não Não Não Não
cotgx 0 0 0 0
existe existe existe existe existe
Figura 3.18: f(x)=cotg x
Observando o gráfico da função f(x)=cotgx, no intervalo
[-2 π ,2 π ], representada na figura 3.18, tem-se que:
124](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-124-320.jpg)
![Trigonometria e Números Complexos
A função é periódica de período π .
Quando x tende aos valores em que a cotg x não existe,
o gráfico da cotangente tende ao infinito positivo ou
negativo.
O estudo da variação nos mostra que no intervalo
[-2 π ,2 π ], f(x)=cotg x é sempre decrescente.
O domínio da função f(x)=cotg x é
D( f ) = ]−2π , −π [∪ ]−π , 0[∪ ]0, π [∪ ]π , 2π [ .
A imagem da função f(x)=cotg x é Im(f)=IR.
3π π π 3π
Nos intervalos −2π , − , −π , − , 0; e π ; ,
2
2 2 2
a função f(x)=cotg x assume valores positivos.
3π π
No intervalo − , −π , − 0 , π ; π e 3π ; 2π a
2
2 2 2
função f(x)=cotg x assume valores negativos.
A função f(x)=cotg x é ímpar pois cotg x=-cotg (-x).
Generalizando, tem-se:
O domínio da função f(x)=cotg x é
D( f ) = {x ∈ IR|x ≠ kπ , k ∈ Z}.
A imagem da função f(x)=cotg x é Im(f)=IR .
Acompanhe, a seguir, alguns exemplos envolvendo a cotangente.
1) Determine o valor de cot g 37π .
6
Solução:
Primeiramente, calcula-se a 1ª determinação positiva de 37π :
6
37π 36π π
= +
6 6 6
37π
Temos que π rad é a primeira determinação positiva de .
6 6
π 3
cos
37π π 6 = 2 = 3 .2 = 3
Então: cot g = cot g =
6 6 sen π 1 2 1
6 2
Unidade 3 125](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-125-320.jpg)




![Universidade do Sul de Santa Catarina
Logo:
1
sec x = , (cos x ≠ 0)
cos x
Utilizando semelhança de triângulos, novamente temos que, o
∆OM’M é semelhante ao ∆OMD.
OD OM
=
OM MM'
OD 1
=
1 sen x
OD . sen x = 1
1
OD =
sen x
Logo:
1
cos ec x = , ( sen x ≠ 0)
sen x
Gráfico da Função Secante
Seja f(x) = sec x
Inicialmente, constrói-se a tabela 3.11, usando a relação
1
sec x = , com x variando [−2π , 2π ].
cos x
Tabela 3.11: Valores da secante
3π π π 3π
x -2π − -π − 0 π 2π
2 2 2 2
Não Não Não Não
secx 1 -1 1 -1 1
existe existe existe existe
130](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-130-320.jpg)
![Trigonometria e Números Complexos
Figura 3.20: f(x)=sec x
Observando o gráfico da função f(x)=sec x, representada na figura
3.20, no intervalo [−2π , 2π ], tem-se que:
A função é periódica de período 2 π .
O domínio da função f(x)=secx é:
3π 3π π π π π 3π 3π
D( f ) = −2π , − ∪ − , − ∪ − , ∪ , ∪ , 2π
2 2 2 2 2 2 2 2
A imagem da função f(x)=sec x é Im(f)= ]−∞; −1]∪ [1; +∞[.
A função f(x)=sec x é crescente nos intervalos
3π 3π π π
−2π , − 2 , − 2 , −π ,
0, 2 e 2 , π .
A função f(x)=sec x é decrescente nos intervalos
π π 3π 3π
−π , − , − , 0 , π , e , 2π .
2 2 2 2
3π π π 3π
Nos intervalos −2π , − , − , e ; 2π , temos
2 2 2 2
sec x ≥ 1.
Nos intervalos − 3π , − π e π ; 3π , sec x ≤ -1.
2
2 2 2
A função f(x)=sec x é par, pois, sec x = sec (-x).
Unidade 3 131](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-131-320.jpg)
![Universidade do Sul de Santa Catarina
Generalizando, tem-se:
O domínio da função f(x)=sec x é
π
D( f ) = x ∈ IR | x ≠ + kπ , k ∈ Z .
2
A imagem da função f(x)=sec x é Im(f)= ]−∞; −1]∪ [1; +∞[.
Gráfico da Função Cossecante
Seja f(x) = cosec x
Inicialmente, constrói-se a tabela 3.12, usando a relação
1
cos ecx = , com x variando [-2π, 2π].
senx
Tabela 3.12: Valores da cossecante
3π π π 3π
x -2π − -π − 0 π 2π
2 2 2 2
Não Não Não Não Não
cosecx 1 -1 1 -1
existe existe existe existe existe
132](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-132-320.jpg)
![Trigonometria e Números Complexos
Figura 3.21: f(x)=cosec x
Observando o gráfico da função f(x)=cosec x, no intervalo
[-2 π ,2 π ], representada na figura 3.21’, temos que:
A função é periódica de período 2 π .
O domínio da função f(x)=cosec x é:
D( f ) = ]−2π , −π [∪ ]−π , 0[∪ ]0, π [∪ ]π , 2π [ .
A imagem da função f(x)=cosec x é
Im (f)= ]−∞; −1]∪ [1; +∞[.
A função f(x)=cosec x é crescente nos intervalos
3π π π 3π
− 2 , −π , −π , − 2 , 2 ,π e
π , 2 .
A função f(x)=cosec x é decrescente nos intervalos
3π π π 3π
−2π , − 2 , − 2 , 0 , 0, 2 e 2 , 2π .
Nos intervalos ]−2π , −π [ e ]0, π [ , temos cosecx ≥ 1.
Nos intervalos ]−π ;0[ e ]π , 2π [, cosecx ≤ -1.
A função f(x)=cosecx é ímpar, pois, cosec (-x) = -cosec x.
Unidade 3 133](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-133-320.jpg)
![Universidade do Sul de Santa Catarina
Generalizando, tem-se:
O domínio da função f(x)=cosec x é
D(f) = {x ∈ IR | x ≠ kπ , k ∈ Z }.
A imagem da função f(x)=cosec x é
Im(f)= ]−∞; −1]∪ [1; +∞[.
Acompanhe alguns exemplos envolvendo as funções secante e
cossecante.
9π
1) Determine o valor de sec .
2
Solução:
9π
Primeiramente, calcula-se a 1ª determinação positiva de rad .
2
9π 8π π
= +
2 2 2
9π π
A primeira determinação positiva de rad é rad .
2 2
9π π
Então: sec = sec → não existe
2 2
9π
Logo, sec → não existe .
2
59π
2) Determine o valor de cos ec .
4
Solução:
59π
Primeiramente, calcula-se a 1ª determinação positiva de .
4
3π
Tem-se que rad é a primeira determinação positiva de
4
59π
rad .
4
59π 3π π
Assim, cos ec = cos ec = cos ec = 2 .
4 4 4
59π
Logo: cos ec = 2.
4
134](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-134-320.jpg)


![Trigonometria e Números Complexos
Função Arco Seno
π π
Redefine-se a função f(x) = sen x para o domínio − , e,
2 2
tem-se a função inversa da função seno como y = arc sen x, se, e
somente se, sen y = x, onde se tem que para cada x ∈ [−1, 1]
π π
corresponde y ∈ − , .
2 2
Observe o gráfico da função y = arc sen x, representado na figura
3.23:
Figura 3.23 : Função y = arc sen x
A partir do gráfico, na figura 3.23, tem-se as seguintes
características da função
y = arc sen x:
o domínio da função é D = [-1,1];
π π
a imagem da função é − , ;
2 2
é crescente em todo seu domínio.
Unidade 3 137](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-137-320.jpg)
![Universidade do Sul de Santa Catarina
Função Arco Cosseno
Da mesma forma, vamos redefinir a função f(x) = cos x para o
domínio [0,π].
A função inversa da função cosseno é definida como y = arc cos x,
se, e somente se, cos y = x, onde se tem que para cada x ∈ [−1, 1]
corresponde y ∈ [0, π ] .
Observe o gráfico da função y = arc cos x, representado na figura
3.24:
Figura 3.24: Função y = arc cos x
A partir do gráfico, na figura 3.24, tem-se as seguintes
características da função
y = arc cos x:
o domínio da função é D = [-1,1];
a imagem da função é [0,π ];
é decrescente em todo seu domínio.
138](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-138-320.jpg)
![Universidade do Sul de Santa Catarina
Função Arco Cotangente
A função inversa da função cotangente é definida como
π
y = arc cotg x = − arc tgx , onde, para cada x real, corresponde
2
y ∈ ]0, π [ .
Observe o gráfico da função y = arc cotg x, representado na figura
3.26:
Figura 3.26: Função y = arc cotg x
A partir do gráfico, na figura 3.26, tem-se as seguintes
características da função y = arc cotg x:
o domínio da função é D = IR;
a imagem da função ∈ ]0, π [ ;
yé
é decrescente em todo seu domínio.
Função Arco Secante
A função inversa da função secante é definida como
1
y = arc sec x = ar cos , onde, para cada x real, tal que x ≥ 1 ,
x
corresponde y = [0, π ] com y ≠ π .
140 2](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-140-320.jpg)
![Trigonometria e Números Complexos
Observe o gráfico da função y = arc sec x, representado na figura
3.27:
Figura 3.27: Função y = arc sec x
A partir do gráfico, na figura 3.27, tem-se as seguintes
características da função y = arc sec x:
o domínio da função é D = {x ∈ IR | | x | ≥ 1};
π
a imagem da função é [0, π ] e y ≠ ;
2
é crescente em todo o seu domínio, ]−∞, −1]∪ [1, +∞[.
Função Arco Cosecante
A função inversa da função cossecante é definida como
1
y = arccos x = arsen , onde, para cada x real, tal que, x ≥ 1 ,
x
π π
corresponde y = − , com y ≠ 0.
2 2
Observe o gráfico da função y = arc cosec x, representado na figura
3.28:
Unidade 3 141](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-141-320.jpg)
![Universidade do Sul de Santa Catarina
Figura 3.28: Função y = arc cosec x
A partir do gráfico, na figura 3.28, tem-se as seguintes
características da função y = arc cosec x:
o domínio da função é D = {x ∈ IR | | x | ≥ 1};
a imagem da função é − π , π e y ≠ 0;
2 2
é decrescente em todo o seu domínio, ]−∞, −1]∪ [1, +∞[.
Que tal alguns exemplos?
Exemplos:
1
1) Qual o valor de y = sec 2 arcsen ?
2
Solução:
1
y = sec 2 arcsen .
2
1
Fazendo x = arcsen , deve-se procurar um arco cujo seno é igual
2
142](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-142-320.jpg)
![Trigonometria e Números Complexos
a 1.
2
π
Então, o arco procurado deve ser x = rad , pois, de acordo com
6
π π
a definição, o arco deve pertencer ao intervalo − , .
2 2
1
Dessa forma, substituindo x em y = sec 2 arcsen , pode-se
2
escrever:
1 π π 1 1
sec 2 arcsen = sec 2 = sec = = = 2.
2 6 3 cos π 1
3 2
1
Logo, o valor de y = sec 2 arcsen é 2.
2
− 2
2) Qual o valor de E = 10. sen arccos
?
2
Solução:
− 2
E = 10. sen arccos
2
− 2
Fazendo x = ar cos , deve-se procurar um arco cujo cosseno é
2
igual a − 2 .
2
3π
Então, o arco procurado deve ser x = rad , pois, de acordo com
4
a definição, o arco deve pertencer ao intervalo [0,π ].
− 2
Dessa forma, substituindo x em E = 10. sen arccos
, pode-
2
se escrever:
− 2
E = 10. sen arccos
2
3π
E = 10. sen
4
2
E = 10.
2
E = 5 2.
Unidade 3 143](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-143-320.jpg)


















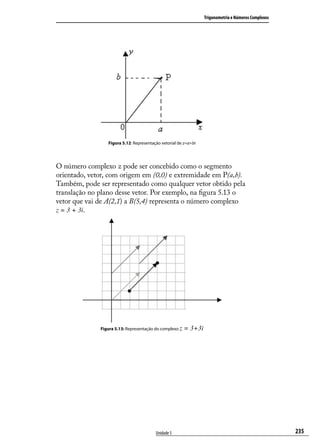
![Universidade do Sul de Santa Catarina
d 2 ( A, B ) = ( xB − x A ) 2 + ( yB − y A ) 2
d ( A, B ) = (xB − x A )2 + (yB − y A )2 .
Seja a figura 4.3:
Figura 4.3: Cosseno da diferença de arcos
Na circunferência trigonométrica tem-se:
os arcos a e b;
o arco a-b;
M representa a extremidade do arco a;
N representa a extremidade do arco b;
P representa a extremidade do arco a-b;
A representa a extremidade do arco nulo.
Observando a figura, conclui-se que as distâncias entre os pontos
P e A, M e N são iguais.
Escreve-se então: d 2 ( P, A) = d 2 ( M , N )
( X P − X A ) + (YP − YA ) = ( X M − X N ) + (YM − YN )
2 2 2 2
[1]
164](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-164-320.jpg)
![Trigonometria e Números Complexos
Note que:
as coordenadas do ponto P são: P(cos(a-b), sen(a-b));
as coordenadas do ponto M são: M(cosa,sena);
as coordenadas do ponto N são: N(cosb,senb);
as coordenadas do ponto A são: A(1,0).
Assim substituindo em [1] tem-se:
[cos(a − b) − 1] + [sen(a − b) − 0] = [cos a − cos b] + [sena − senb]
2 2 2 2
Desenvolvendo a equação e sabendo que:
sen 2 (a − b) + cos 2 (a − b) = 1 ;
sen 2 a + cos 2 a = 1 ;
sen 2b + cos 2 b = 1 .
Para facilitar o desenvolvimento da equação, vamos nomear seus membros
A e B, então:
A = cos (a − b ) − 1 + sen (a − b ) − 0 e B = [cos a − cos b ] + [sen a − sen b ] .
2 2 2 2
Desenvolvendo A, tem-se:
2 2
A = cos (a − b ) − 1 + sen (a − b ) − 0
A = cos 2 (a − b ) − 2 cos (a − b ) + 1 + sen 2 (a − b )
A = 2 − 2 cos (a − b )
Desenvolvendo B, tem-se:
B = [cos a − cos b ] + [sen a − sen b ]
2 2
B = cos 2 a − 2.cos a.cos b + cos 2 b + sen 2 a − 2.sen a.sen b + sen 2b
B = 2 − 2 (cos a.cos b + sen a.sen b )
Como A=B, tem-se:
2 − 2 cos(a − b) = 2 − 2 (cos a.cos b + sen a.sen b )
Unidade 4 165](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-165-320.jpg)
![Universidade do Sul de Santa Catarina
Para simplificar a equação, divide-se por (-2):
−1 + 1cos(a − b) = −1 + (cos a.cos b + sen a.sen b)
Logo :
cos(a − b) = cos a.cos b + sen a.sen b
As outras três fórmulas decorrem facilmente da que foi obtida.
cos(a + b) = cos a.cos b − sen a.sen b
Demonstração:
Substituindo b por –b tem-se:
cos (a − (−b) ) = cos a.cos(−b) + sen a.sen (−b) [2]
Você deve lembrar que seno é uma função ímpar e cosseno é par.
Logo, tem-se:
sen (−b) = − sen b .
cos(−b) = cos b .
Substituindo em [2] tem-se:
cos(a + b) = cos a.cos b − sen a.sen b .
Na seqüência, acompanhe a fórmula do seno da diferença e do
seno da soma:
Seno da diferença: sen (a − b) = sen a.cos b − cos a.sen b .
Demonstração:
Para esta demonstração, utiliza-se um teorema auxiliar:
Para todo x real, tem-se:
π
cos − x = senx
2
π
sen − x = cos x.
2
166](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-166-320.jpg)
![Trigonometria e Números Complexos
Dessa forma:
sen(a − b) = sen a.cos b − cos a.sen b
π
sen (a − b ) = cos − (a − b )
2
π
sen (a − b ) = cos − a + b
2
π π
sen (a − b ) = cos − a .cos b − sen − a .senb
2 2
sen (a − b ) = sena.cos b − cos a.senb.
Seno da soma: sen (a + b) = sen a.cos b + cos a.sen b .
Demonstração:
Substituindo b por –b, tem-se:
sen (a + b) = sen (a − (−b) ) = sen a.cos (−b) − cos a.sen (−b) [3]
Lembre-se que seno é uma função ímpar e cosseno é par.
Logo:
sen(−b) = − senb .
cos(−b) = cos b .
Substituindo em [3], tem-se:
sen (a + b) = sen a.cos b + cos a.sen b .
Finalmente, acompanhe as fórmulas da tangente da soma e da
diferença de dois arcos.
tga − tgb
tg (a − b) = .
1 + tga.tgb
Demonstração:
senx
Você já conhece a relação fundamental tgx = .
cos x
Na demonstração a seguir, ela será utilizada.
Unidade 4 167](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-167-320.jpg)








![Universidade do Sul de Santa Catarina
As diferentes equações possuem nomes específicos em função
de suas características específicas. Por exemplo: 2 x − 4 = 9 é
denominada equação irracional, pois contém a incógnita “x” sob
o radical.
Nesta seção, serão trabalhadas as equações trigonométricas que
recebem este nome porque são equações em que figuram as
funções trigonométricas com um arco desconhecido.
Para resolvermos as equações trigonométricas, devemos utilizar
artifícios e transformações que nos permitam chegar a equações
básicas do tipo senx=a, cosx=a e tgx=a, com a ∈ IR. Dessa forma,
podemos obter a variável “x” conhecendo o valor de a.
Veja agora alguns exemplos de equações trigonométricas:
a ) sen x = 0
b) 1 − cos 2 x + sen x = 0
c) sen 2 x = 2.cos x
Vale ressaltar que a solução de uma equação trigonométrica é o
conjunto dos valores da variável x que, caso existam, satisfazem a
equação dada.
Observe como encontrar o conjunto solução de algumas equações
trigonométricas:
1
1) Resolver a equação sen x = no intervalo [0,2π ].
2
Solução:
Você já sabe que o seno é positivo no primeiro e segundo
quadrante.
1 π
O arco cujo seno corresponde a é no primeiro quadrante e,
2 6
utilizando a simetria, pode-se encontrar o outro arco do segundo
quadrante: π − π = 5π .
6 6
Observe a representação da solução na figura 4.5.
176](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-176-320.jpg)
![Trigonometria e Números Complexos
1
Figura 4.5: sen x = ; [0; 2π ]
2
π 5π
Logo, a solução desta equação é S = , .
6 6
1
2) Resolver a equação sen x = , com x ∈ 0, π .
2 2
Observe que está sendo resolvida a mesma equação, porém com
intervalo de solução diferenciado. A figura 4.6 representa a
situação do problema.
1 π
Figura 4.6: sen x = ;x ∈ 0, 2
2
π 1 π
Logo, como sen = , então a solução é S = .
6 2 6
Unidade 4 177](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-177-320.jpg)


![Universidade do Sul de Santa Catarina
5) Dê a solução da equação sen 2x=2cos x no intervalo [0; 2π ].
Solução:
Utilizando a identidade do seno do arco duplo, tem-se:
sen 2 x = 2 cos x
2.sen x.cos x = 2 cos x
Resolvendo a equação:
2.sen x.cos x − 2.cos x = 0
2.cos x.( sen x − 1) = 0.
Você já sabe que o produto entre dois fatores só é nulo quando
um dos fatores for zero. Dessa forma:
2.cos x = 0 ou sen x − 1 = 0.
Assim, tem-se duas equações para resolver:
2.cos x = 0 sen x − 1 = 0
ou
cos x = 0 sen x = 1
Encontrando a solução para cos x = 0, no intervalo dado tem-se:
π 3π
x= ou x = .
2 2
Encontrando a solução para sen x = 1, no intervalo dado tem-se:
π
x= .
2
Logo, a solução da equação sen 2 x = 2 cos x no intervalo [0, 2π ] é
S = π , 3π .
2 2
180](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-180-320.jpg)


![Trigonometria e Números Complexos
2
Figura 4.9: cos x < −
2
Logo, a solução será:
3π 5π
S = x ∈ IR | <x< .
4 4
3) Qual é a solução da inequação tg x > 3 no intervalo [0, 2π ]?
Solução:
Figura 4.10: tgx > 3
Unidade 4 183](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-183-320.jpg)





![Trigonometria e Números Complexos
18) Qual o valor de (tg 10º + cot g 10º ).sen 20º ?
19) Se tg x + cot g x = 4 , quanto vale sen 2 x ?
2
20) Sendo a + b = 45º e tg a = , calcule tg b .
3
21) Resolver a equação sen 2 x + sen x − 2 = 0 para 0 ≤ x ≤ 2π .
22) No intervalo [0,π ], qual a solução da equação tg x − 1 = 0 .
Unidade 4 189](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-189-320.jpg)


















![Universidade do Sul de Santa Catarina
1) Considere os números complexos z1 = 2-2i e z2 = 1+3i e efetue
as seguintes operações:
a) (z1+z2)2
Solução:
(z1+z2)2 = [(2-2i)+(1+3i)]2
(z1+z2)2 = (3+i) 2
(z1+z2)2 = 32+2.3.i+i2
(z1+z2)2 = 9+6i+(-1)
(z1+z2)2 = 8+6i
b) (z2 ) .z1
2
Solução:
(z2 ) .z1 = (1 + 3i ) . (2 + 2i )
2 2
(z2 ) .z1 = (1 + 6i + 9i 2 ). (2 + 2i )
2
(z2 ) .z1 = (1 + 6i-9) . (2 + 2i )
2
(z2 ) .z1 = (−8 + 6i ). (2 + 2i )
2
(z2 ) .z1 = −16 − 16i + 12i + 12i
2 2
(z2 ) .z1 = −16 − 4i + 12.(−1)
2
(z2 ) .z1 = −28 − 4i
2
2) Determine o número complexo z, tal que i.z + (z + z) = 1 + 2i .
Solução:
Sabe-se que z=a+bi e , logo, substituindo na igualdade
i.z + (z + z) = 1 + 2i temos:
208](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-208-320.jpg)
![Trigonometria e Números Complexos
i.(a+bi)+[(a-bi)+(a+bi)]=1+2i
ai+bi2+2a = 1+2i
2a - b +ai = 1+2i
Utilizando-se a igualdade entre dois números complexos
obtém-se:
2a − b = 1
a=2
Substituindo, tem-se:
Logo, o número complexo z procurado é z = 2 + 3i.
3) Encontre o valor de x de modo que z = (2x+3i)2 seja um
imaginário puro.
Solução:
Desenvolvendo o produto notável na expressão (2x+3i)2 tem-se:
(2x+3i)2 = 4x2 + 12xi +9i2
(2x+3i)2 = 4x2 + 12xi - 9
(2x+3i)2 = (4x2 -9) + 12xi
Você já sabe que para que um número complexo seja imaginário
puro deve ter Re(z)=0 e Im(z) ≠ 0.
Unidade 5 209](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-209-320.jpg)




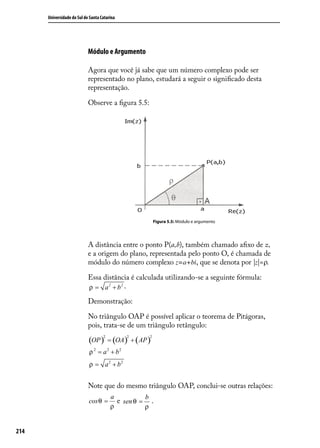







![Universidade do Sul de Santa Catarina
π
Logo, θ = rad ou θ = 45o .
4
Portanto, a forma trigonométrica de z=2+2i é:
z = ρ .(cos θ + isen θ )
π π
z = 2 2 . cos + isen
4 4
2) Escreva na forma algébrica o número complexo
z=5.(cos270º + i sen270º).
Solução:
Inicialmente calcula-se o valor do cos270º e sen270º.
cos270º = 0 e sen270º = -1
Agora se substitui esses valores no complexo
z = 5.(cos 270º +i.sen 270º )
z = 5.[0 + i.(−1)]
z = 5.(0 − i )
z = −5i
Portanto, a forma algébrica de z = 5.(cos 270º +isen270º ) é z=-5i.
Operações na forma trigonométrica ou polar
Multiplicação
Sejam os números complexos
z1 = ρ1(cosθ1 + isenθ1) e
z2 = ρ2(cosθ2 + isenθ2)
Efetuando a multiplicação entre z1 e z2 , tem-se:
z1. z2 = ρ1 (cosθ1 + isenθ1) . ρ2 (cosθ2 + isenθ2)
z1. z2=ρ1. ρ2 (cosθ1. cosθ2 + icosθ1. senθ2+ isenθ1. cosθ2+ i2senθ1.senθ2)
z1. z2=ρ1. ρ2 [(cosθ1.cosθ2-senθ1.senθ2) + i(cosθ1.senθ2+ senθ1.cosθ2)]
222](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-222-320.jpg)
![Trigonometria e Números Complexos
Utilizando as transformações trigonométricas, estudadas na unidade
4, tem-se:
z1. z2 =ρ1. ρ2 [cos(θ1+θ2)+isen(θ1+θ2)]
Note que para efetuar a multiplicação basta multiplicar os módulos e
somar os argumentos dos complexos.
Exemplo:
π π
Efetue z1. z2 , sendo z1 = 3. cos + i.sen e
3 3
2π 2π
z2 = 2.(cos + i.sen ) .
3 3
Solução:
Dos complexos retira-se os seguintes dados:
π
ρ1 = 3 e θ1 = 3
ρ = 2 e θ = 2π
2
2
3
Substituindo-se esses dados em z1. z2 =ρ1. ρ2[cos(θ1+θ2)+isen(θ1+θ2)]
tem-se:
π 2π π 2π
z1 .z2 = 3.2. cos + + isen +
3 3 3 3
3π 3π
z1 .z2 = 6. cos + isen
3 3
z1 .z2 = 6. (cos π + isenπ )
Divisão
Sejam os números complexos
z1 = ρ1(cosθ1 + isenθ1) e z2 = ρ2 (cosθ2 + isenθ2) com z2 ≠ 0
Unidade 5 223](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-223-320.jpg)











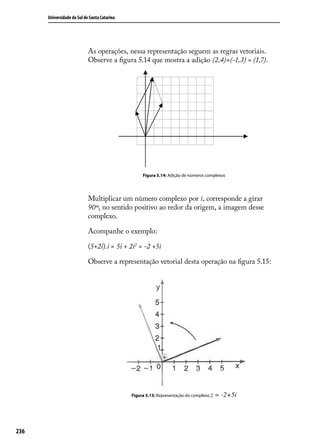




![Trigonometria e Números Complexos
8) Determine o valor real de x para que o produto
(12 – 2i).[18 + (x – 2).i] seja também um número real.
9) Dado o complexo z = a + bi. A soma de z com seu conjugado é 18 e o
produto de ambos é 145. Determine o módulo de ab.
10) Calcule a e b reais de modo que i 250 + i104 + 2i 37 = a + bi .
11) Calcule a potência de i para i8 n + 3, tal que n ∈ N*.
(2 + i )101.(2 − i )50
12) Simplificando , obtém-se:
(−2 − i )100 .(i − 2) 49
Unidade 5 241](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-241-320.jpg)














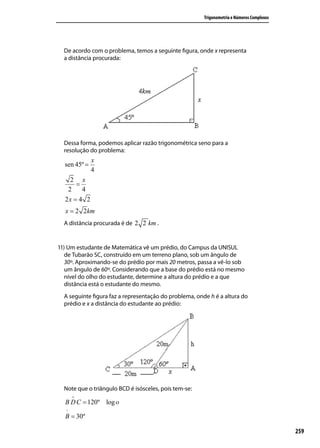


















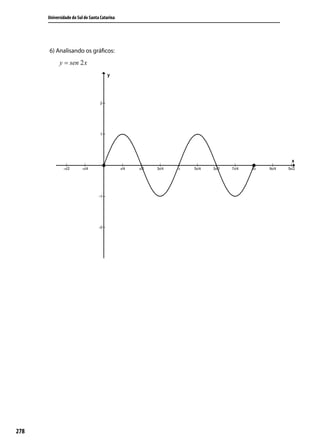
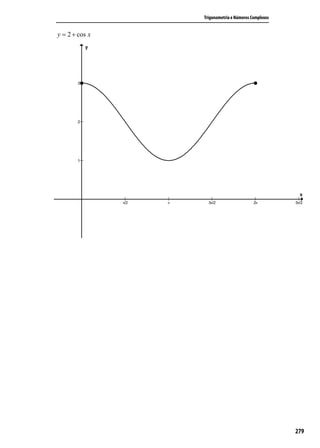
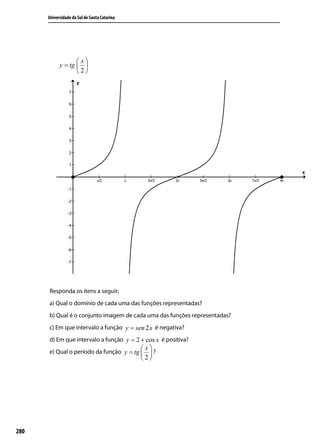
![Trigonometria e Números Complexos
a) y = sen 2 x D=R
y = 2 + cos x D=R
x
y = tg D = { x ∈ R / x ≠ π + k 2π }
2
b) y = sen 2 x Im = [ −1,1 ]
y = 2 + cos x Im = [ 1,3 ]
x
y = tg Im = ] − ∞ , ∞ [
2
π 3π
c) 2 ;π e 2 , 2π
d ) [0; 2π ]
e ) P = 2π
7) Determine o valor de k sabendo que sen x = 3k - 7.
Sabe-se que −1 ≤ sen x ≤ 1 , tem-se:
−1 ≤ senx ≤ 1
−1 ≤ 3k − 7 ≤ 1
7 − 1 ≤ 3k − 7 + 7 ≤ 1 + 7
6 ≤ 3k ≤ 8 (÷3)
6 3k 8
≤ ≤
3 3 3
8
2≤k ≤
3
8
Logo: k ∈ R | 2 ≤ k ≤
3
8) Qual a imagem da função f(x) = 5 + cos x?
f ( x) = 5 + cos x
a=5
b =1
a − b = 5 −1 = 4
a + b = 5 +1 = 6
Im = [4, 6]
281](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-281-320.jpg)
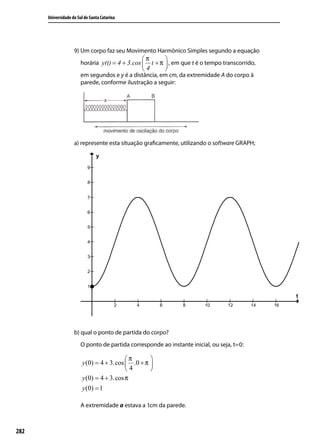


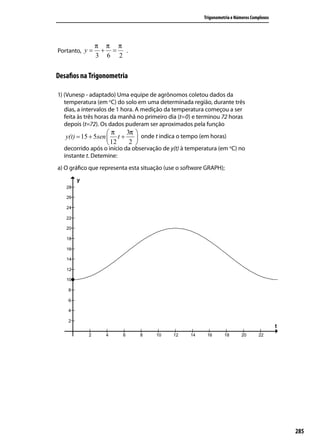















![Trigonometria e Números Complexos
21) Resolver a equação sen 2 x + sen x − 2 = 0 para 0 ≤ x ≤ 2π .
sen 2 x + senx − 2 = 0 0 ≤ x ≤ 2π
Observe que esta equação representa uma equação do 2o grau cuja a incógnita é sen x,
portanto pode - se utilizar a fórmula resolutiva deste tipo de equação :
∆ = 12 − 4.1.(−2 )
∆ = 1+ 8 = 9
−1 ± 9
senx =
2.1
−1 ± 3
senx =
2
4 2
sen x = − = −2 e sen x = = 1
2 2
Como −1 ≤ senx ≤ 1 então senx = 1
π
Portanto, x=
2
π
S =
2
22) No intervalo [0,π ], qual a solução da equação tg x − 1 = 0 .
301](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-301-320.jpg)

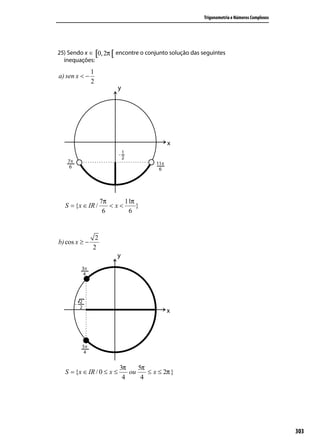
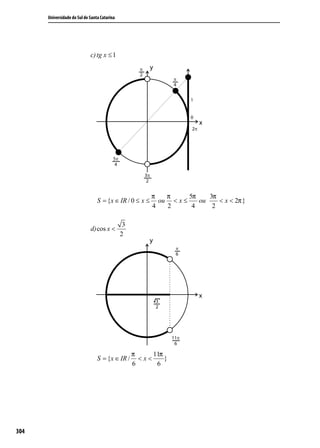




![Trigonometria e Números Complexos
5) Efetue:
a) (2 – i).(1 + 3i)
(2 − i ).(1 + 3i ) = 2 + 6i − i − 3i 2 = 2 + 6i − i + 3 = 5 + 5i .
1 1
b) + i . − i
2 2
1 1 1 1 1 2 1 1+ 4 5 .
− i . + i = − i + i − i = + 1 = =
2 2 4 2 2 4 4 4
c) (1 + i).(2 – i).(1 + 2i)
(1 + i ).(2 − i ) .(1 + 2i ) = 2 − i + 2i − i 2 .(1 + 2i ) = [2 − i + 2i + 1].(1 + 2i ) = (3 + i ).(1 + 2i ) =
3 + 6i + i + 2i 2 = 3 + 6i + i − 2 = 1 + 7i.
6) Expresse os seguintes números complexos na forma a+bi:
−2 + i (−2 + i ) −2i 4i − 2i 2 4i + 2 1 + 2i
a) = . = = = .
2i 2i −2i −4i 2 4 2
2i (4 + 2i ) (2 + 2i ) 8 + 4 ( 2) i
2
2
4+ 2i + 2 2i + 8 + 6 2i − 2 6 + 6 2i
b) = . = = = = 1 + 2i.
2i (2 − 2i ) (2 + 2i ) ( 2i )
2
2− 4− 4+2 6
(1 + i )
2
1 + 2i + i 2 1 + 2i − 1 2i (2 + i ) 4i + 2i 2 4i − 2 2 4
c) = = = . = 2
= = − + i.
2−i 2−i 2−i (2 − i ) (2 + i ) 4−i 4 +1 5 5
3
7) Qual o conjugado do número complexo z = ?
1 + 2i
Inicialmente coloca-se z na forma a + bi:
z=
3
.
(1 − 2i ) = 3 − 6i = 3 − 6i = 3 − 6 i
(1 + 2i ) (1 − 2i ) 1 − 4i 2 1 + 4 5 5
3 6 3 6
Como z = − i ⇒ z = + i.
5 5 5 5
309](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-309-320.jpg)
![Universidade do Sul de Santa Catarina
8) Determine o valor real de x para que o produto
(12 – 2i).[18 + (x – 2).i] seja também um número real.
Inicialmente escreve-se o número complexo dado na forma a + bi:
(12 − 2i ). 18 + (x − 2 )i = 216 + 12i.( x − 2) − 36i − 2i 2 . (x − 2 )
(12 − 2i ). 18 + (x − 2 )i = 216 + 12 xi − 24i − 36i + 2 x − 4
(12 − 2i ). 18 + (x − 2 )i = 212 + (12 x − 60)i
Dessa forma tem-se:
Im( z ) = 0 ⇒ 12 x − 60 = 0
12 x = 60
60
x=
12
x=5
9) Dado o complexo z = a + bi. A soma de z com seu conjugado é 18 e o
produto de ambos é 145. Determine o módulo de ab.
Expressando estas informações na linguagem matemática, tem-se:
z + z = 18
z.z = 145
Se z = a + bi, tem − se que z = a − bi. Substituindo no sistema, tem-se:
z + z = 18
a + bi + a − bi = 18
2a = 18
a=9
z.z = 145
(a + bi ).(a − bi ) = 145
a 2 − (bi ) = 145
2
92 − b 2i 2 = 145
81 + b 2 = 145
b 2 = 145 − 81
b 2 = 64
b = ± 64
b = ±8
Portanto, o módulo de a.b = 9.( ± 8) = 72.
310](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-310-320.jpg)





![Universidade do Sul de Santa Catarina
19) Calcule:
a) (1 – i) 6
3 3
(1 − i ) = (1 − i ) = 1 − 2i + i 2 = [1 − 2i − 1] = (−2i ) = −8i 3 = −8.(−i ) = 8i
6 2 3 3
b) 100
1 3
2 2 i
− +
1 3
z = − +i
2 2
1 3
n = 100 , a = − , b =
2 2
ρ = a 2 + b2
2 2
1 3 1 3
ρ = − + = + =1
2 2
4 4
1
−
a 1
cos θ = ⇒ cos θ = 2 = −
ρ 1 2
3
b 3
sen θ = ⇒ sen θ = 2 =
ρ 1 2
θ = 120o
z n = ρ n .[cos( nθ ) + i.sen( nθ )]
( )
z100 = 1100 . cos 100.120o + i.sen( 100.120o )
z100 = cos 12000o + i.sen12000o
Calcula-se a primeira determinação positiva de 12000 o :
z100 = cos 120o + i.sen120o
Faz-se a redução ao primeiro quadrante para o arco de 120 o
z100 = − cos 60o + i.sen60o
1 3
z100 = − + i.
2 2
316](https://image.slidesharecdn.com/aptrigonometrianumeroscomplexo-111212024552-phpapp01/85/Ap-trigonometria-numeros-complexo-316-320.jpg)