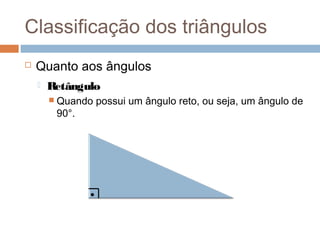
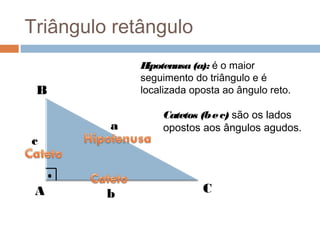
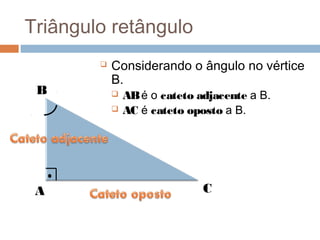
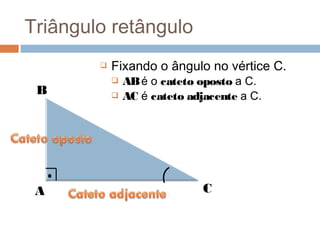
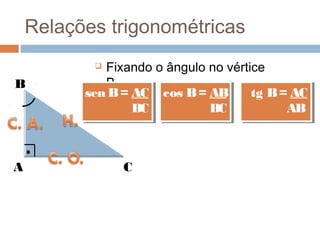
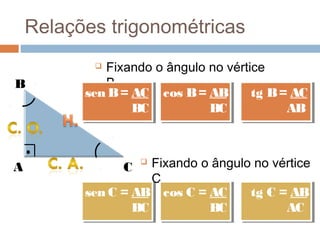
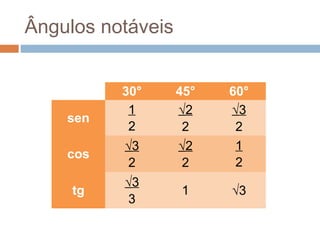
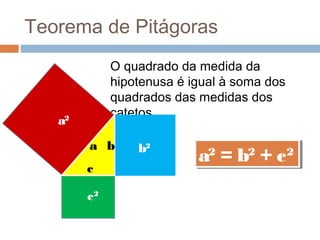
O documento apresenta os conceitos básicos de triângulos, classificando-os em equilátero, isósceles e escaleno de acordo com os lados, e em retângulo, agudo e obtuso de acordo com os ângulos. Também define as relações trigonométricas de seno, cosseno e tangente para ângulos de triângulos retângulos e apresenta o Teorema de Pitágoras.

1. TRIGONOMETRIA
Triângulo

2. Etimologia
três, três vezes Latim a ng ulum
e s q uina , d o bra , c a nto

3. Classificação dos triângulos
 Quanto aos lados
 Equilátero
 Vem do Latim a e q ui, “igual”, mais la te ra lis , “relativo a
lado”, de la tus , “lado”.
 Tem três lados iguais.

4. Classificação dos triângulos
 Isósceles
 Vem do Grego is o s , “igual”, mais s ke lo s , “perna”, aqui
com o sentido de “lado”.
 Tem dois lados iguais e um diferente.

5. Classificação dos triângulos
 Escaleno
 Erachamado, em Grego, s ka le no s , “desigual,
desparelho, grosseiro”, de s ka lle in, “cortar, limpar
vegetação”.
 Tem todos os lados diferentes.

6. Classificação dos triângulos
 Quanto aos ângulos
 Retângulo
 Quando possui um ângulo reto, ou seja, um ângulo de
90°.

7. Classificação dos triângulos
 Acutângulo
 Quandopossui os três ângulos agudos, ou seja,
menor do que 90°.

8. Classificação dos triângulos
 Obtusângulo
 Quando possui ângulo obtuso, ou seja, maior do que
90°.

9. Triângulo retângulo
 Chamamos de triâ ng ulo re tâ ng ulo àquele que
possui ângulo reto, isto é, medindo 90°.
 Os ângulos agudos são complementares, pois
somam 90°.
 Os lados recebem nomes específicos: c a te to s
e hip o te nus a .

10. Triângulo retângulo
H ipotenusa (a): é o maior
seguimento do triângulo e é
B localizada oposta ao ângulo reto.
Catetos (b e c) são os lados
a opostos aos ângulos agudos.
c
A b C

11. Triângulo retângulo
 Considerando o ângulo no vértice
B.
B  AB é o cateto adjacente a B.
 AC é cateto oposto a B.
A C

12. Triângulo retângulo
 Fixando o ângulo no vértice C.
 AB é o cateto oposto a C.
B  AC é cateto adjacente a C.
A C

13. Relações trigonométricas
seno de um ângulo = cateto oposto ao ângulo
hipotenusa
cosseno de um ângulo = cateto adjacente ao
ângulo
hipotenusa
tangente de um ângulo = cateto oposto ao
ângulo
hipotenusa

14. Relações trigonométricas
 Fixando o ângulo no vértice
B B.
sen B = AC cos B = AB
sen B = AC cos B = AB tg B = AC
tg B = AC
BC
BC BC
BC AB
AB
A C

15. Relações trigonométricas
 Fixando o ângulo no vértice
B B.
sen B = AC cos B = AB
sen B = AC cos B = AB tg B = AC
tg B = AC
BC
BC BC
BC AB
AB
A C
Fixando o ângulo no vértice
C.
sen C = AB cos C = AC
sen C = AB cos C = AC tg C = AB
tg C = AB
BC
BC BC
BC AC
AC

16. Ângulos notáveis
30° 45° 60°
1 √2 √3
sen
2 2 2
√3 √2 1
cos
2 2 2
√3
tg 1 √3
3

17. Teorema de Pitágoras
O quadrado da medida da
hipotenusa é igual à soma dos
quadrados das medidas dos
catetos.
a2
a b b2
a2 = b2 + c2
a2 = b2 + c2
c
c2

18. Referências
 http://origemdapalavra.com.br/palavras/triangulo
 http://www.colegioweb.com.br/matematica/classific

19. Acesse o blog e divirta!!!