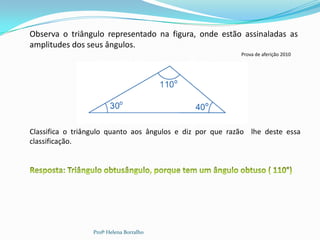
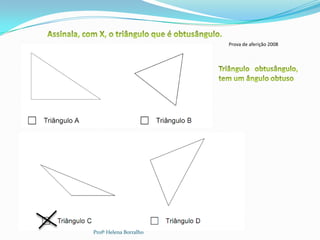
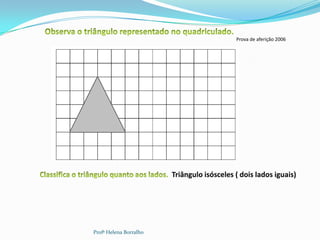
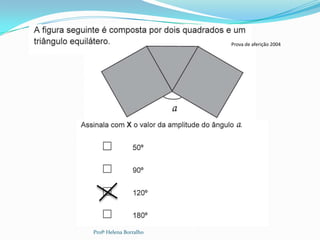
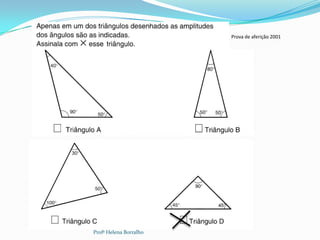
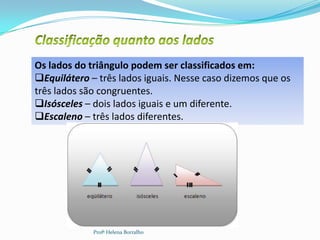
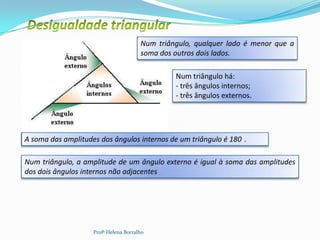
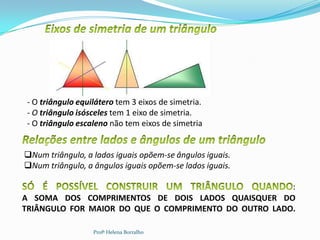
O documento discute as classificações de triângulos com base em seus lados e ângulos, incluindo triângulos equiláteros, isósceles, escalenos, retângulos, agudos e obtusos. Também aborda propriedades como a soma dos ângulos internos e a relação entre ângulos internos e externos.

1. Profª Helena Borralho

2. Os lados do triângulo podem ser classificados em:
Equilátero – três lados iguais. Nesse caso dizemos que os
três lados são congruentes.
Isósceles – dois lados iguais e um diferente.
Escaleno – três lados diferentes.
Profª Helena Borralho

3. Quanto aos ângulos do triângulo podem ser classificados em:
 Retângulo – quando possui um ângulo reto
Acutângulo – quando possui os três ângulos agudos.
Obtusângulo – quando possui um ângulo obtuso.
Profª Helena Borralho

4. Num triângulo, qualquer lado é menor que a
soma dos outros dois lados.
Num triângulo há:
- três ângulos internos;
- três ângulos externos.
A soma das amplitudes dos ângulos internos de um triângulo é 180 .
Num triângulo, a amplitude de um ângulo externo é igual à soma das amplitudes
dos dois ângulos internos não adjacentes
Profª Helena Borralho

5. Utilizando os dados da figura, calcula:
1. A medida de cada um dos ângulos internos do triângulo [MNP];
2. A soma dos ângulos externos do triângulo.
Considerando que os ângulos Como a soma dos ângulos internos de um
seguintes são suplementares, triângulo é um ângulo raso, vem:
temos
Considerando que os ângulos seguintes são
suplementares, temos:
Profª Helena Borralho

6. O triângulo [ABC] é retângulo em A;
[AH] é perpendicular a [BC] e o ângulo externo
em C mede 130º.
Calcula a medida da amplitude dos ângulos x, y
e z.
Amplitude do ângulo c= 180º-130º= 50º
Amplitude do ângulo x= 180º-(90º+50)= 40º
Amplitude do ângulo y= 90º-40= 50º
Amplitude do ângulo z= 180º - (90º+50)= 40º
Profª Helena Borralho

7. - O triângulo equilátero tem 3 eixos de simetria.
- O triângulo isósceles tem 1 eixo de simetria.
- O triângulo escaleno não tem eixos de simetria
Num triângulo, a lados iguais opõem-se ângulos iguais.
Num triângulo, a ângulos iguais opõem-se lados iguais.
:
A SOMA DOS COMPRIMENTOS DE DOIS LADOS QUAISQUER DO
TRIÂNGULO FOR MAIOR DO QUE O COMPRIMENTO DO OUTRO LADO.
Profª Helena Borralho

8. Há três maneiras diferentes de construir
triângulos!
Vamos fazê-lo com a ajuda destes três
amigos: a régua, o compasso e o
transferidor.
Profª Helena Borralho

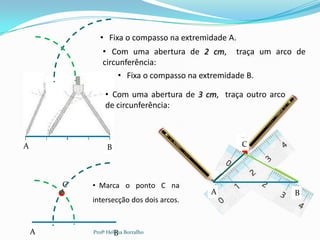
9. Para esta construção, vamos utilizar a régua e o compasso.
De um triângulo [ABC], sabemos que:
AB 4 cm BC 3 cm AC 2 cm
• Com a régua, traça o segmento de reta [AB] com 4 cm
de comprimento.
• Marca os pontos A e B.
A B
Profª Helena Borralho

10. • Fixa o compasso na extremidade A.
• Com uma abertura de 2 cm, traça um arco de
circunferência:
• Fixa o compasso na extremidade B.
• Com uma abertura de 3 cm, traça outro arco
de circunferência:
C
C
A B
C • Marca o ponto C na
A B
intersecção dos dois arcos.
A B
Profª Helena Borralho

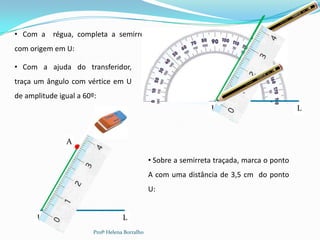
11. Para esta construção, deves utilizar a régua e o transferidor.
De um triângulo [LUA], sabemos que:
UL 4 cm UA 3,5 cm ˆ
LUA 60
• Com a régua, traça o segmento de reta [UL] com 4 cm de
comprimento.
• Marca os pontos U e L.
U L 11
Profª Helena Borralho

12. • Com a régua, completa a semirreta
com origem em U:
• Com a ajuda do transferidor,
traça um ângulo com vértice em U
de amplitude igual a 60º:
U L
A
• Sobre a semirreta traçada, marca o ponto
A com uma distância de 3,5 cm do ponto
U:
U L
Profª Helena Borralho

13. • Une agora o ponto L ao ponto A:
A
U L
Profª Helena Borralho

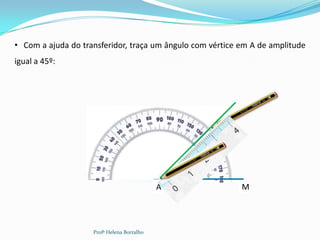
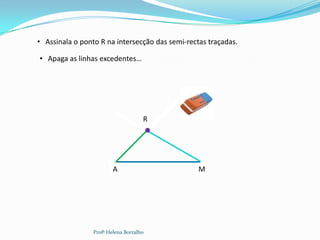
14. Para esta construção, deves utilizar a régua e o transferidor.
De um triângulo [MAR], sabemos que:
AM 4,5 cm ˆ
MAR 45 ˆ
AMR 30
• Com a régua, traça o
segmento de reta [AM] com 4,5
cm de comprimento.
• Marca os pontos A e M.
A M
• Com a régua, completa a 14
semirreta com origem em A.
Profª Helena Borralho

15. • Com a ajuda do transferidor, traça um ângulo com vértice em A de amplitude
igual a 45º:
A M
Profª Helena Borralho

16. • Com a régua, completa a semi-recta com origem em M:
• Com a ajuda do transferidor, traça um ângulo com vértice em M de
amplitude igual a 30º:
A M
Profª Helena Borralho

17. • Assinala o ponto R na intersecção das semi-rectas traçadas.
• Apaga as linhas excedentes…
R
A M
Profª Helena Borralho

18. Observa o triângulo representado na figura, onde estão assinaladas as
amplitudes dos seus ângulos.
Prova de aferição 2010
Classifica o triângulo quanto aos ângulos e diz por que razão lhe deste essa
classificação.
Profª Helena Borralho

19. A Maria desenhou um triângulo acutângulo. Qual das opções seguintes
contém as amplitudes dos ângulos do triângulo que a Maria desenhou?
Prova de aferição 2009
Profª Helena Borralho

20. Prova de aferição 2008
Profª Helena Borralho

21. Prova de aferição 2006
Triângulo isósceles ( dois lados iguais)
Profª Helena Borralho

22. Prova de aferição 2005
Profª Helena Borralho

23. Prova de aferição 2004
Profª Helena Borralho

24. Prova de aferição 2001
Profª Helena Borralho