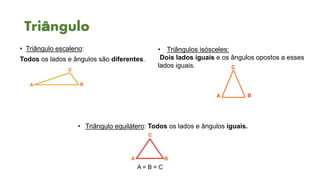
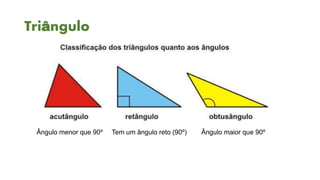
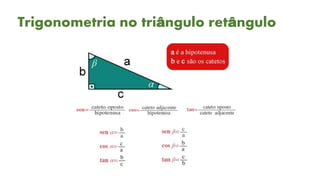
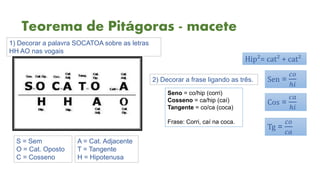
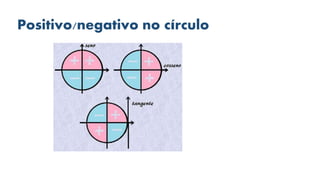
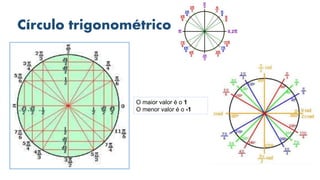
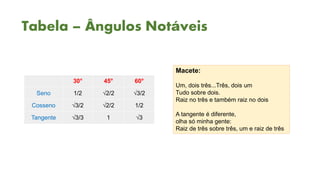
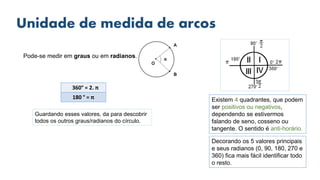
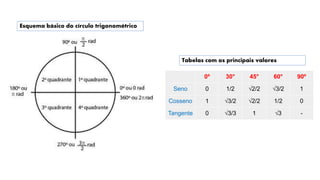
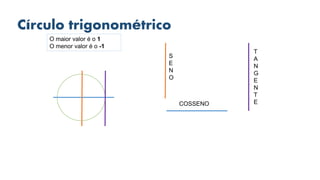
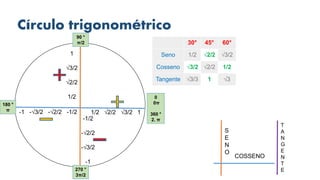
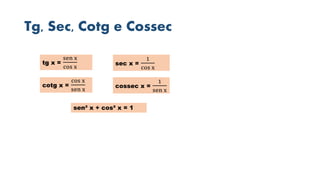
1) O documento aborda conceitos básicos de trigonometria, incluindo tipos de triângulos, teorema de Pitágoras, funções trigonométricas e suas relações no círculo trigonométrico. 2) São apresentados exemplos numéricos ilustrando aplicações das funções seno, cosseno e tangente em triângulos retângulos. 3) As tabelas de valores notáveis e as relações fundamentais entre as funções trigonométricas são explicadas detalhadamente.

1. • Triângulos
• Trigonometria no triângulo retângulo
• Teorema de Pitágoras
• Relação Fundamental
• sen, cos e tg
• Racionalizar
• Unidade de medida de arcos
• Círculo Trigonométrico
• Relação Fundamental e arcos complementares
• Tangente, seno, cosseno, secante, cossecante e cotangete

2. Triângulo
• Triângulo escaleno:
Todos os lados e ângulos são diferentes.
• Triângulos isósceles:
Dois lados iguais e os ângulos opostos a esses
lados iguais.
• Triângulo equilátero: Todos os lados e ângulos iguais.
A = B = C

3. Triângulo
Ângulo menor que 90º Tem um ângulo reto (90º) Ângulo maior que 90º

4. Trigonometria no triângulo retângulo

5. Teorema de Pitágoras
Hip²= cat² + cat²
O seno de um ângulo no triângulo retângulo é a razão entre o cateto
oposto e a hipotenusa.
O cosseno de um ângulo no triângulo retângulo é a razão entre o
cateto adjacente e a hipotenusa.
A tangente de um ângulo no triângulo retângulo é a razão entre o
cateto oposto e o cateto adjacente.
Hip²= cat² + cat²
Sen =
𝑐𝑜
ℎ𝑖
Cos =
𝑐𝑎
ℎ𝑖
Tg =
𝑐𝑜
𝑐𝑎

6. Teorema de Pitágoras - macete
Hip²= cat² + cat²
Sen =
𝑐𝑜
ℎ𝑖
Cos =
𝑐𝑎
ℎ𝑖
Tg =
𝑐𝑜
𝑐𝑎
1) Decorar a palavra SOCATOA sobre as letras
HH AO nas vogais
S = Sem
O = Cat. Oposto
C = Cosseno
A = Cat. Adjacente
T = Tangente
H = Hipotenusa
Seno = co/hip (corri)
Cosseno = ca/hip (caí)
Tangente = co/ca (coca)
Frase: Corri, caí na coca.
2) Decorar a frase ligando as três.

7. Tabela – Ângulos Notáveis
30° 45° 60°
Seno 1/2 √2/2 √3/2
Cosseno √3/2 √2/2 1/2
Tangente √3/3 1 √3
Macete:
Um, dois três...Três, dois um
Tudo sobre dois.
Raiz no três e também raiz no dois
A tangente é diferente,
olha só minha gente:
Raiz de três sobre três, um e raiz de três

8. Triângulo retângulo - exemplos
Exemplo 1. Sabendo que sen α =1/2 , determine o valor de x no triângulo retângulo abaixo:
Solução: A hipotenusa do triângulo é x e o lado com medida conhecida é o cateto oposto ao ângulo α.
Assim, temos que:

9. Triângulo retângulo - exemplos
Exemplo 2. Determine os valores de seno, cosseno e tangente dos ângulos agudos do triângulo
abaixo.
Solução: Temos que:

10. Triângulo retângulo - exemplos
Exemplo 3. Num triângulo retângulo a hipotenusa mede 8cm, e um dos ângulos internos possui
30°. Qual o valor dos catetos oposto (x) e adjacente (y) desse triângulo?
De acordo com as relações trigonométricas, o seno é representado pela seguinte relação:
Sen = cateto oposto/hipotenusa
Sen 30° = x/8
½ = x/8
2x = 8
X = 8/2
X = 4
Logo, o cateto oposto desse triângulo retângulo mede 4 cm.
A partir disso, se a hipotenusa = cateto oposto/cateto adjacente, tem-se:
hip = Co/Ca
8 = 4/y
8y=4
y = ½

11. Relação Fundamental
sen² α + cos² α = 1
Exemplo 4 : Sendo sen α = 3/5 , calcule cos α e tg α.
sen² α + cos² α = 1
(3/5)² + cos² α = 1
9/25 + cos² α = 1
cos² α = 1 – 9/25
cos² α =
25−9
25
= 16/25
cos α =± 16/25 = 4/5
OBS: A raiz sempre pode
ser positiva ou negativa
tg α =
𝐒𝐄𝐍 α
cos α
Tg α = 3/5 : 4/5
Tg α = 3/5 . 5/4
Tg α = 3/4

14. Racionalizar
Sempre que a raiz ficar em baixo, deve-se racionalizar, ou seja,
utilizar um método para que essa raiz fique em cima.
Suponha que, ao final da conta, seu resultado deu
Para racionalizar, basta multiplicar esse resultado com a
própria raiz ( 5) em forma fração.
Ao multiplicar duas raízes com o mesmo número, a raiz é eliminada.

15. Unidade de medida de arcos
Pode-se medir em graus ou em radianos.
360° = 2. π
180 ° = π
Guardando esses valores, da para descobrir
todos os outros graus/radianos do círculo.
Existem 4 quadrantes, que podem
ser positivos ou negativos,
dependendo se estivermos
falando de seno, cosseno ou
tangente. O sentido é anti-horário.
Decorando os 5 valores principais
e seus radianos (0, 90, 180, 270 e
360) fica mais fácil identificar todo
o resto.

16. Cálculo dos radianos

17. Cálculo dos radianos

18. Positivo/negativo no círculo

19. Círculo trigonométrico
O maior valor é o 1
O menor valor é o -1

20. 0º 30° 45° 60° 90º
Seno 0 1/2 √2/2 √3/2 1
Cosseno 1 √3/2 √2/2 1/2 0
Tangente 0 √3/3 1 √3 -
Esquema básico do círculo trigonométrico
Tabelas com os principais valores

21. Círculo trigonométrico
O maior valor é o 1
O menor valor é o -1
S
E
N
O
COSSENO
T
A
N
G
E
N
T
E

22. Círculo trigonométrico
S
E
N
O
COSSENO
T
A
N
G
E
N
T
E
-1 -√3/2 -√2/2 -1/2
1
√3/2
√2/2
1/2
30° 45° 60°
Seno 1/2 √2/2 √3/2
Cosseno √3/2 √2/2 1/2
Tangente √3/3 1 √3
-1/2
-√2/2
-√3/2
-1
1/2 √2/2 √3/2 1
180 °
π
0
0π
360 °
2. π
90 °
π/2
270 °
3π/2

23. Relação fundamental
sen² x + cos² x = 1
Arcos complementares
Quando a soma dos arcos é igual a 90°.
Exemplo: sen 85° e cos 5º ; sem 20º e cos 70º.
sen x = cos ( π
2
− x )
cos x = sen ( π
2
− x )

24. Relação fundamental
Arcos complementares
Exemplo 5 - Dado sem x = 1/3, com
π
2
< x < π , calcule cos x.
Primeiro, vemos onde está localizado o X.
Sen²x + cos² x = 1
1/3² + cos²x = 1
cos² x = 1 – 1/9 = 9-1/9
cos x =± 8/9 =
−2. 2
3
O resultado final é negativo, pois o cos do 1º quadrante é
negativo.
π
𝛑
𝟐 Está no primeiro
quadrante, onde
cos é negativo e
sen é positivo.
Exemplo 6 – Sabendo que sen 70° = 2,
calcule cos 20°.
Como são arcos complementares
(70+20 = 90) o resultado será o
mesmo para os dois.
Assim, cos 20° = 2.

25. Tg, Sec, Cotg e Cossec
tg x =
sen x
cos x
cotg x =
cos x
sen x
sec x =
1
cos x
cossec x =
1
sen x
sen² x + cos² x = 1