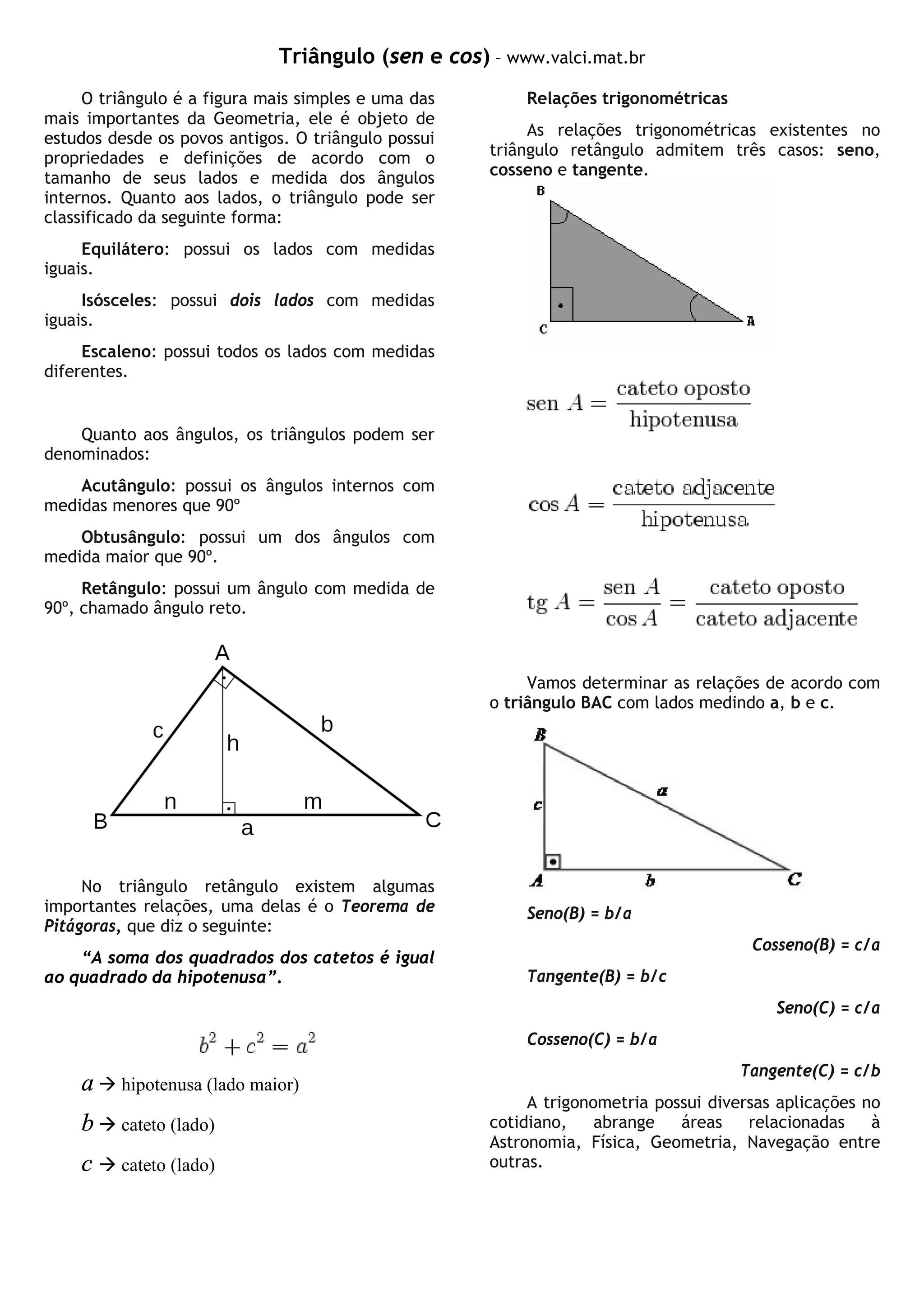
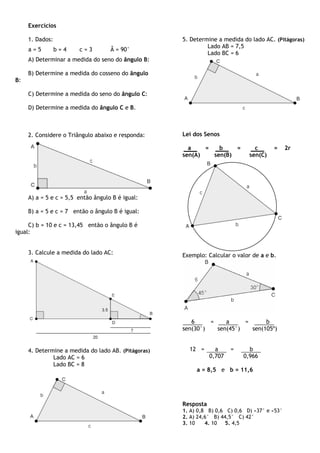
O documento discute o triângulo, suas propriedades e relações trigonométricas. Ele define os tipos de triângulos de acordo com o tamanho de seus lados e ângulos, e explica as relações de seno, cosseno e tangente em triângulos retângulos. Ele fornece exemplos para calcular medidas de lados e ângulos usando essas relações.

1. Triângulo (sen e cos) – www.valci.mat.br
O triângulo é a figura mais simples e uma das Relações trigonométricas
mais importantes da Geometria, ele é objeto de
estudos desde os povos antigos. O triângulo possui As relações trigonométricas existentes no
propriedades e definições de acordo com o triângulo retângulo admitem três casos: seno,
tamanho de seus lados e medida dos ângulos cosseno e tangente.
internos. Quanto aos lados, o triângulo pode ser
classificado da seguinte forma:
Equilátero: possui os lados com medidas
iguais.
Isósceles: possui dois lados com medidas
iguais.
Escaleno: possui todos os lados com medidas
diferentes.
Quanto aos ângulos, os triângulos podem ser
denominados:
Acutângulo: possui os ângulos internos com
medidas menores que 90º
Obtusângulo: possui um dos ângulos com
medida maior que 90º.
Retângulo: possui um ângulo com medida de
90º, chamado ângulo reto.
Vamos determinar as relações de acordo com
o triângulo BAC com lados medindo a, b e c.
No triângulo retângulo existem algumas
importantes relações, uma delas é o Teorema de Seno(B) = b/a
Pitágoras, que diz o seguinte:
Cosseno(B) = c/a
“A soma dos quadrados dos catetos é igual
ao quadrado da hipotenusa”. Tangente(B) = b/c
Seno(C) = c/a
Cosseno(C) = b/a
Tangente(C) = c/b
a à hipotenusa (lado maior)
A trigonometria possui diversas aplicações no
b à cateto (lado) cotidiano, abrange áreas relacionadas à
Astronomia, Física, Geometria, Navegação entre
c à cateto (lado) outras.

2. Exercícios
1. Dados: 5. Determine a medida do lado AC. (Pitágoras)
Lado AB = 7,5
a=5 b=4 c=3 Â = 90°
Lado BC = 6
A) Determinar a medida do seno do ângulo B:
B) Determine a medida do cosseno do ângulo
B:
C) Determine a medida do seno do ângulo C:
D) Determine a medida do ângulo C e B.
2. Considere o Triângulo abaixo e responda: Lei dos Senos
a = b = c = 2r
sen(A) sen(B) sen(C)
A) a = 5 e c = 5,5 então ângulo B é igual:
B) a = 5 e c = 7 então o ângulo B é igual:
C) b = 10 e c = 13,45 então o ângulo B é
igual:
3. Calcule a medida do lado AC: Exemplo: Calcular o valor de a e b.
6 = a = b
sen(30°) sen(45°) sen(105º)
4. Determine a medida do lado AB. (Pitágoras) 12 = a = b
Lado AC = 6 0,707 0,966
Lado BC = 8
a = 8,5 e b = 11,6
Resposta
1. A) 0,8 B) 0,6 C) 0,6 D) ≈37° e ≈53°
2. A) 24,6° B) 44,5° C) 42°
3. 10 4. 10 5. 4,5