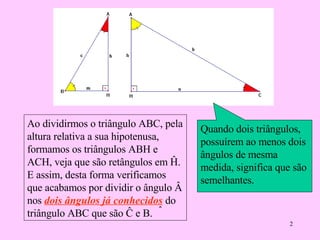
1) O documento discute as relações métricas em triângulos retângulos, dividindo o triângulo pela altura em dois novos triângulos semelhantes. 2) As proporções dos lados dos triângulos semelhantes levam a equações relacionando os lados dos diferentes triângulos. 3) A soma das projeções da hipotenusa sobre os catetos é igual à hipotenusa, relacionando ao Teorema de Pitágoras.

1. Relações Métricas no Triângulo ( Δ) Retângulo. Observe que o triângulo ABC é retângulo em Â, isto é a medida de  é 90º, e como a soma dos ângulos internos de qualquer triângulo é 180º, concluímos que a soma dos ângulos B e Ĉ é 90º. ˆ Ângulo de 90º

2. Quando dois triângulos, possuírem ao menos dois ângulos de mesma medida, significa que são semelhantes. Ao dividirmos o triângulo ABC, pela altura relativa a sua hipotenusa, formamos os triângulos ABH e ACH, veja que são retângulos em Ĥ. E assim, desta forma verificamos que acabamos por dividir o ângulo  nos dois ângulos já conhecidos do triângulo ABC que são Ĉ e B. ˆ

3. Observem agora os lados deste triângulo. Lado AB Lado BC Lado AC O lado AB “ vai do ângulo de 90º até o ângulo pintado de amarelo”. O lado AC “ vai do ângulo de 90º até o ângulo pintado de vermelho”. O lado BC “ vai do ângulo pintado de amarelo até o ângulo pintado de vermelho”. Ângulo de 90º

4. Observe que dividimos o triângulo ABC em dois novos triângulos ABH e ACH, que são semelhantes entre si, pois seus ângulos são congruentes “iguais” e seus lados são proporcionais.

5. Vamos agora comparar o triângulo ABC com o triângulo ABH. Como são semelhantes, seus lados são proporcionais, logo temos as seguintes relações: Lados do Δ ABC Lados do Δ ABH

6. Deduzimos as seguintes relações: 2ª) bm = ch 3ª) cc = am 1ª) ah = cb Não se esqueça que: “para passar o número que esta dividindo para o outro lado do sinal de igual o fazemos passar, multiplicando do outro lado”. Das proporções obtidas dos lados dos Δs semelhantes que são:ABC e ABH.

7. Comparando o triângulo ABC com o triângulo ACH. Como são semelhantes, seus lados são proporcionais, logo temos as seguintes relações: Lados do Δ ABC Lados do Δ ACH

8. Das proporções obtidas dos lados dos Δs semelhantes que são:ABC e ACH. Deduzimos as seguintes relações: 1ª) bh = cn 2ª) bb = an 3ª) bc = ah

9. Comparando o triângulo ABH com o triângulo ACH. Lados do Δ ABH Lados do Δ ACH Como são semelhantes, seus lados são proporcionais, logo temos as seguintes relações:

10. Das proporções obtidas dos lados dos Δs semelhantes que são:ABH e ACH. Deduzimos as seguintes relações: 1ª) bh = cn 2ª) ch = bm 3ª) hh = mn

11. Imagine estas projeções sendo como o sol “batendo”numa ripa de madeira inclinada numa parede, isto produz uma sombra, a qual chamaremos de projeção. Outra relação métrica é: a = m + n , ou seja m (segmento BH) é a projeção do cateto c sobre a hipotenusa e n (segmento CH) é a projeção do cateto b sobre a hipotenusa, logo a soma de m (BH) + n (CH) é igual a hipotenusa a (segmento BC).

12. Teorema de Pitágoras Hipotenusa Cateto Cateto Ângulo de 90º Os lados AB e AC do Δ ABC são chamados de Catetos. O lado BC do Δ ABC é contrário (está de frente) com o ângulo de 90º, por esse motivo leva o nome especial de Hipotenusa.

13. Temos a relação: hipotenusa ao quadrado é igual a soma dos quadrados dos catetos. Hip 2 = cat 2 + cat 2 a 2 = b 2 + c 2 Teorema de Pitágoras.

14. Resumo das fórmulas das relações métricas no Δ retângulo. 1ª) ah = bc 2ª) c 2 = am 3ª) bm = ch 4ª) bh = cn 5ª) b 2 = an 6ª) h 2 = mn 7ª) a = m + n 8ª) a 2 = b 2 + c 2

15. Espero que tenham gostado da aula em slides: Autor: Prof. Jose Fabio Braga Szmelcynger. E-mail: fabio@uli.com.br - fone 0xx1938079073 Data: 22/02/2004. Amparo-SP.