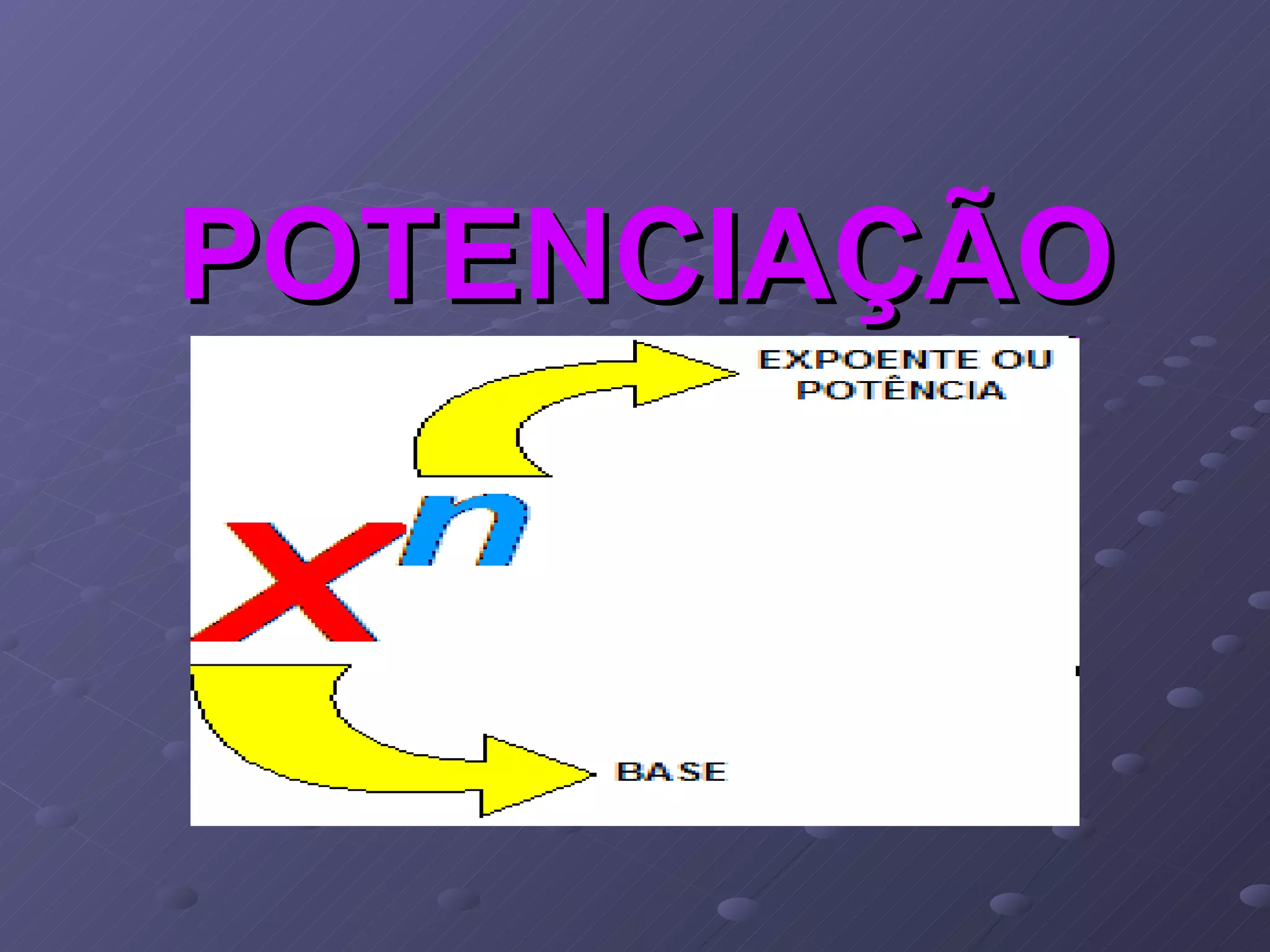
1) Potenciações representam multiplicações repetidas onde os fatores são iguais. 2) Uma potência é representada por baseelevadoaexpoente, onde a base é o fator e o expoente indica a quantidade de vezes que a base é multiplicada. 3) Existem propriedades para cálculo de potenciações, como somar expoentes para multiplicação de bases iguais e distribuir potências em produtos.

1. POTENCIAÇÃO

2. O QUE SÃO AS POTÊNCIAS: As potências surgiram no intuito de representar multiplicações onde os fatores eram iguais. Exemplo: 3 x 3 x 3 x 3 é o 3 vezes ele mesmo 4 vezes Multiplicação com Fatores iguais

3. Representação da Potenciação: Podemos representar a mesma multiplicação da seguinte forma: 3 x 3 x 3 x 3 = 3 4 ↓ Fatores iguais. Essa representação é conhecida como potenciação. Sempre que tivermos fatores iguais, podemos montar uma potência.

4. Representamos uma potência da seguinte forma: base expoente 3 4 =3 x 3 x 3 x 3 = 81 Chamamos de: base sempre valor do fator ; expoente é a quantidade de vezes que o fator se multiplica; potência é o resultado do produto.

5. Como se lê: 10 1 = dez elevado a potência um ou dez elevado a um. 7 2 = sete elevado a ao quadrado ou quadrado de sete. 18 3 = dezoito elevado ao cubo ou cubo de dezoito. 5 4 = cinco elevado a quarta potência, cinco elevado a quarta. 12 5 = doze elevado a quinta potência ou doze elevado a quinta. Nomes especiais: expoente 2 : chamamos de quadrado expoente 3 : chamamos de cubo Essas denominações vieram de: quadrado: área de um quadrado que é o produto de dois fatores iguais cubo: do volume do cubo que é o produto de três fatores iguais

6. Casos especiais: Expoente igual a: 1 (um) Toda potenciação cujo expoente é 1 tem como resultado o valor da base. Exemplo: 7 1 = 7 0 (zero) Toda potenciação cujo expoente é zero o resultado será sempre 1. Exemplo: 12 0 = 1

7. Base igual a: 1 (um) Toda vez que a base for 1, o resultado da potenciação será 1 Exemplo: 1 5 = 1 x 1 x 1 x 1 x 1 = 1 0 (zero) Toda vez que a base for 0, o resultado da potenciação será 0 Exemplo: 0 7 = 0 x 0 x 0 x 0 x 0 x 0 x 0 = 0 10 (dez) Para calcular uma potenciação com base igual a dez basta escrever zeros igual ao número do expoente. Exemplo: 10 8 = 100.000.000 (8 zeros)

8. Propriedades da Potenciação Existem certas regras, ou propriedades, das potenciações, que ao serem aplicadas facilitam o cálculo do resultado.

9. Multiplicação entre Bases Iguais A Regra é: Repete a Base e SOMA os Expoentes . Exemplos : 2 2 . 2 3 = 2 2 + 3 = 2 5 = 2 x 2 x 2 x 2 x 2 = 32 5 1 . 5 3 = 5 1 + 3 = 5 4 = 5 x 5 x 5 x 5 = 625

10. Divisão entre Bases Iguais A Regra é: Repete a Base e SUBTRAI os Expoentes . Exemplos : 2 8 ÷ 2 3 = 2 8- 3 = 2 5 = 2 x 2 x 2 x 2 x 2 = 32 5 7 . 5 3 = 5 7-3 = 5 4 = 5 x 5 x 5 x 5 = 625

11. Potência de Potência Regra é: Repete a Base e MULTIPLICA-SE os Expoentes Exemplos: (8 5 ) 6 = 8 5x6 = 8 30 (15 3 ) 9 = 15 3x9 = 15 27

12. Potência de um Produto Regra: DISTRIBUIR a Potência para as Bases Exemplos: (14 x 9) 5 = 14 5 x 9 5 (21 x 3) 8 = 21 8 x 3 8