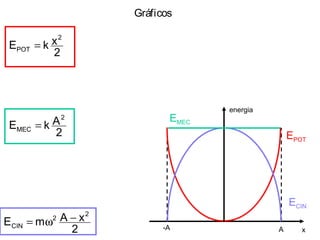
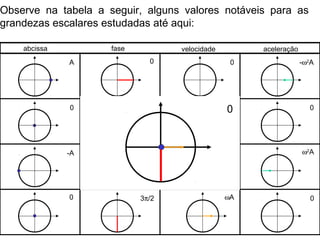
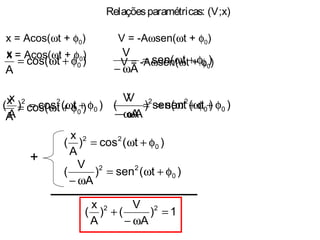
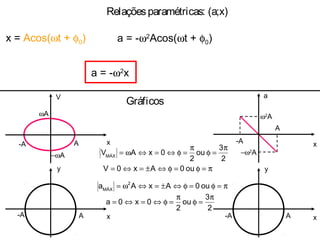
O documento descreve o movimento harmônico simples (MHS) de uma partícula, definindo suas principais características como: x(t) = Acos(ωt + φ0), onde x é a coordenada, A é a amplitude, ω é a frequência angular e φ0 é a fase inicial. Também apresenta as equações para a velocidade v(t) = -Aωsen(ωt + φ0) e aceleração a(t) = -Aω2cos(ωt + φ0), relacionando-as graficamente.

1. Seja P a projeção do movimento
da partícula sobre o eixo 0x.
A coordenada x de P varia com
o tempo segundo a função:
x = Acos(φ)
como
φ = ωt + φ0
temos,
x = Acos(ωt + φ0)
y
xA-A
φ
x
Observe que a função x
é periódica, com
período T e limitada
entre as abcissas -A e
A.
O movimento descrito pela projeção
P é chamado Movimento Harmônico
Simples ou M.H.S.
Podemos dizer então que uma
partícula executa um M.H.S quando
sua funçao horária dos espaços x(t) é
da forma:
x(t) = Acos(ωt + φ0), onde:
A-A
P

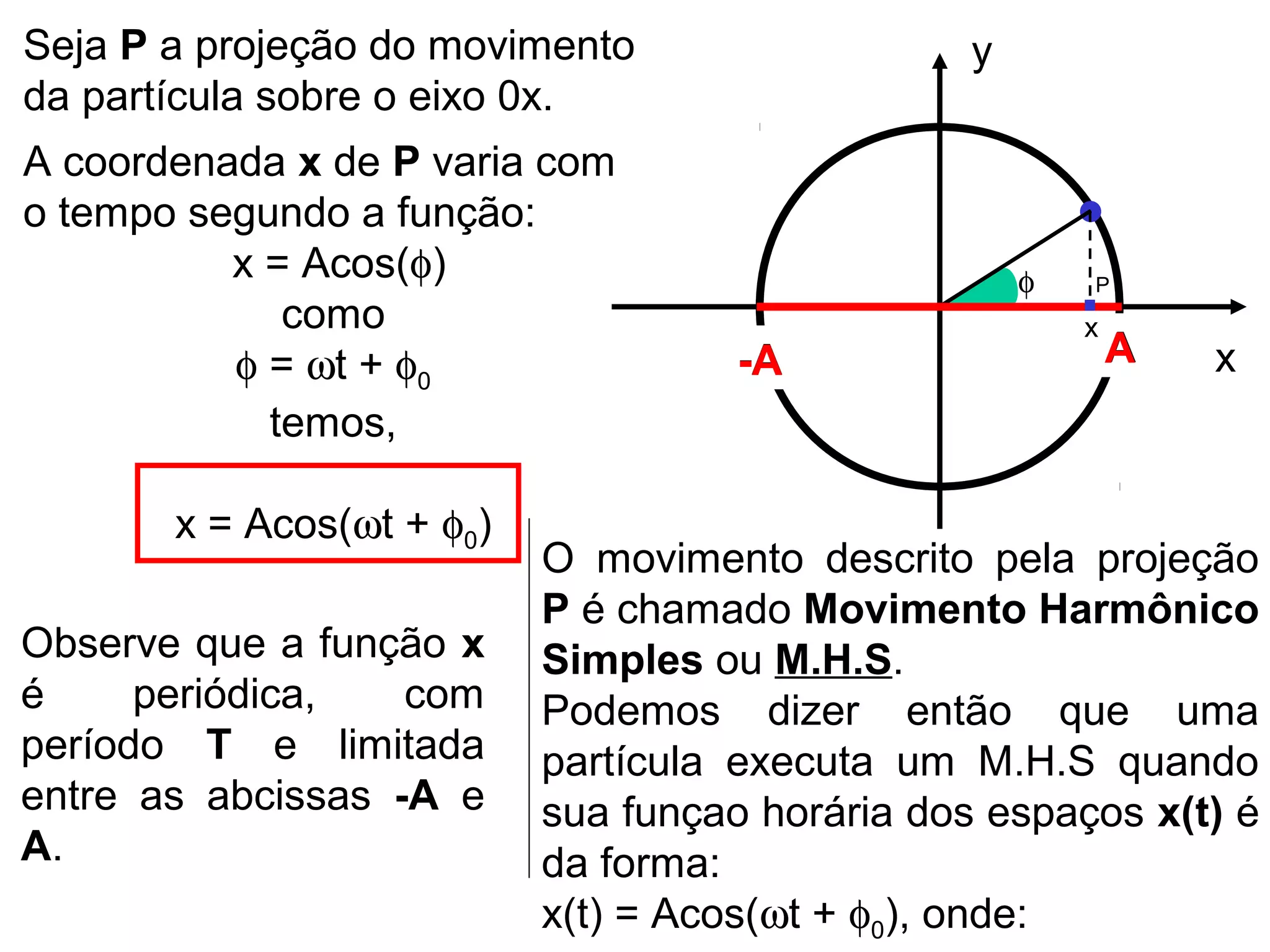
2. x(t) = Acos(ωt + φ0)
A: amplitude do movimento;
A
ωt + φ0 : fase do movimento;
ωt + φ0
ω: pulsação ou freqüência angular do movimento;
ω
φ0: fase inicial do movimento.
φ0
É importante lembrar que:
T
2π
=ω e
T
1
f =
Portanto,
f2
T
2
π=
π
=ω
Unidades
No Sistema Internacional de Unidades
(SI):
[x] = metro (m);
[t] = segundo (s);
[f] = hertz (s-1
ou Hz);
[φ] = radiano (rad);
[ω] = hertz (s-1
ou Hz) *.
* Por uma questão didática, usamos
habitualmente [ω] como rad/s ou rad.s-1
.

3. r
Velocidadeeaceleração escalaresdo M.H.S.
φ P
V
Em um dado instante
t, a partícula ocupa
uma posição angular φ
e possui uma
velocidade vetorial de
intensidade V dada
por:
V = ωA
V
Traçamos sobre a
partícula, uma reta
auxiliar r, paralela ao
eixo 0x. O ângulo
formado entre V e a
perpendicular a r é φ.
Projetando-se V
sobre r, obtemos a
componente na
direção 0x de V. A
intensidade V dessa
componente é dada
por:
V = V senφ
Note que V tem
sentido oposto ao do
Eixo 0X. Daí o sinal
negativo que surge
na expressão de V.
Como,
V = ωA
e
φ = ωt + φ0,
temos:
V = ωAsen(ωt + φ0)
φ
Observe agora a
projeção P da
partícula sobre o
eixo 0x.
Como vimos, P
realiza um M.H.S..
A velocidade
escalar V de P
coincide com a
componente em 0x
de V. Obtemos
assim a função da
velocidade escalar
V de P:
V = -ωΑsen(ωt + φ0)
y
x
- A AV

4. φ
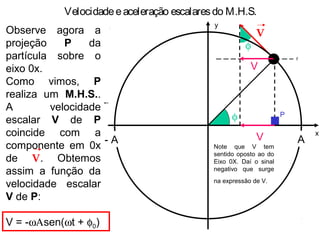
Velocidadeeaceleração escalaresdo M.H.S.
y
x
- A A
φ
Como a partícula
executa M.C.U., ela
possui tão somente
aceleção centripeta acp
de intensidade:
acp = ω2
A
acp
r
Traçamos a reta
auxiliar r pela
extremidade de acp
e paralela ao eixo
0x. O ângulo
formado entre acp e
r é φ.
a = acpcosφ
Obtemos a
componente de acp na
direção 0x fazendo sua
progeçao sobre r:
Como
acp = ω2
A
e
φ = ωt + φ0
temos:
a = acpcosφa = ω2
Acos(ωt + φ0)
a
A projeção P da
partícula sobre o
eixo 0x executa um
M.H.S. e sua
aceleração escalar
coincide com a
componente na
direção 0x de acp.
Portanto:
a= -ω2
Acos(ωt + φ0)
P
a
Note que a tem
sentido oposto ao do
Eixo 0X. Daí o sinal
negativo que surge
na expressão de a.
Unidades
No Sistema Internacional de
Unidades (SI):
[v] = m/s ou m.s-1
;
[a] = m/s2
ou m.s-2
.

5. T/4 T/2 3T/4 T 2T 3T 4T 5T 6T 7T
Gráficos
φ0 = 0
x
t
V
t
a
t
x = Acos(ωt + φ0)
V = -Aωsen(ωt + φ0)
a = -ω2
Acos(ωt + φ0)
A
-A
ω2
A
−ωA
ωA
−ω2
A

6. Observe na tabela a seguir, alguns valores notáveis para as
grandezas escalares estudadas até aqui:
abcissa fase velocidade aceleração
0 π/2 0-ωA
A 0 0 -ω2
A
-A π 0 ω2
A
0 3π/2 0ωA
A0-A0

7. x = Acos(ωt + φ0)
Relaçõesparamétricas: (V;x)
V = -Aωsen(ωt + φ0)x = Acos(ωt + φ0)
)tcos(
A
x
0φ+ω= V = -Aωsen(ωt + φ0))tsen(
A
V
0φ+ω=
ω−
)tcos(
A
x
0φ+ω= )t(cos)
A
x
( 0
22
φ+ω= )tsen(
A
V
0φ+ω=
ω−
)t(sen)
A
V
( 0
22
φ+ω=
ω−
)t(cos)
A
x
( 0
22
φ+ω=
)t(sen)
A
V
( 0
22
φ+ω=
ω−
+
)t(sen)t(cos)
A
V
()
A
x
( 0
2
0
222
φ+ω+φ+ω=
ω−
+ 1)
A
V
()
A
x
( 22
=
ω−
+

8. Relaçõesparamétricas: (a;x)
x = Acos(ωt + φ0) a = -ω2
Acos(ωt + φ0)
a = -ω2
Acos(ωt + φ0)a = -ω2
Acos(ωt + φ0)
x = Acos(ωt + φ0)
a = -ω2
x
Gráficos
y
x-A A
a
-A
A
ω2
A
−ω2
A
x
V
x
x
y
-A A
A-A
ωA
−ωA 2
3
ou
2
0xAVMÁX
π
=φ
π
=φ⇔=⇔ω=
π=φ=φ⇔±=⇔= ou0Ax0V
π=φ=φ⇔±=⇔ω= ou0AxAa 2
MÁX
2
3
ou
2
0x0a
π
=φ
π
=φ⇔=⇔=

9. Osciladores

10. Freqüênciado sistemamassa-mola
A força resultante qua atua no
sistema é a força elástica. Do
Princípio Fundamental da
Dinâmica temos,
FRES = FEL
ma = kx (1)
Como o sistema executa um
M.H.S.:
a = ω2
x (2)
Substituindo (2) em (1) temos,
ma = kx
ma = kxmω2
x = kx
mω2
x = kxmω2
= k
mω2
= k
m
k2
=ω
m
k2
=ω
m
k
=ω
Como ω = 2πf temos,
m
k
=ω
m
k
f2 =π

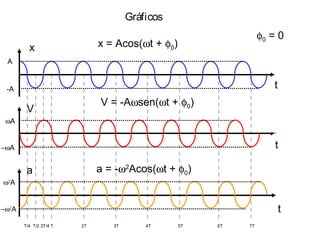
11. Energiano sistemamassa-mola
Sendo o sistema
conservativo, a energia
mecânica é constante:
EMEC = EPOT + ECIN
2
Vm
2
xkE
22
MEC +=
Para x = A ou x = -A
então V = 0, assim:
2
Vm
2
xkE
22
MEC += 0
2
AkE
2
MEC +=
0
2
AkE
2
MEC +=
2
AkE
2
MEC =Na verdade, para qualquer
M.H.S.,
2
AkE
2
MEC =
Unidades
No Sistema Internacional de
Unidades (SI):
[E] = joule ou J.
J = kgm2
/s2
ou kgm2
.s-2
.
2
XkE
2
POT =
2
VmE
2
CIN =

12. Gráficos
2
VmE
2
CIN = 1)
A
V
()
A
x
( 22
=
ω−
+Como
1)
A
V
()
A
x
( 22
=
ω−
+ 22
)
A
x
(1)
A
V
( −=
ω−
22
)
A
x
(1)
A
V
( −=
ω−
2222
xAV ω−ω=
temos,
2
VmE
2
CIN =
2
xAmE
2
2
CIN
−ω=
energia
x-A A2
xAmE
2
2
CIN
−ω=
EPOT
2
xkE
2
POT =
ECIN
2
AkE
2
MEC =
EMEC