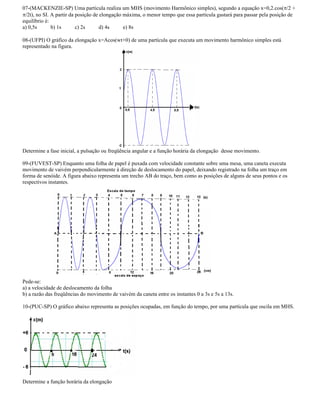
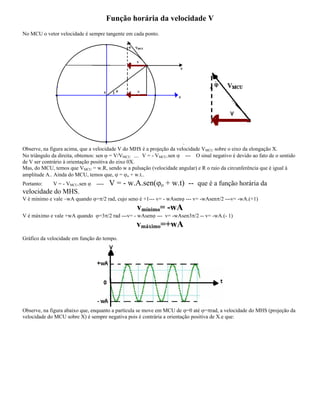
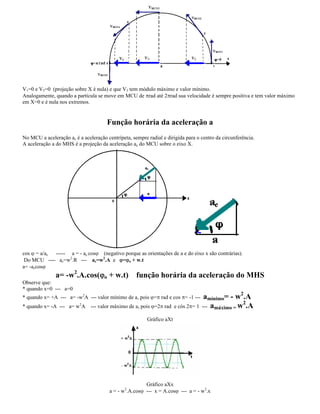
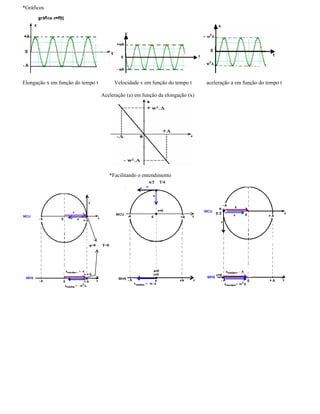
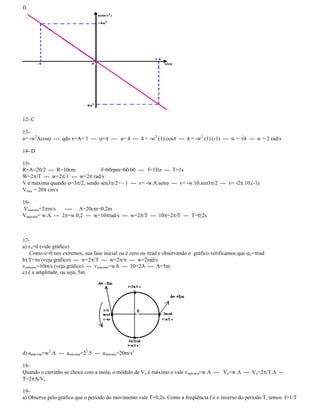
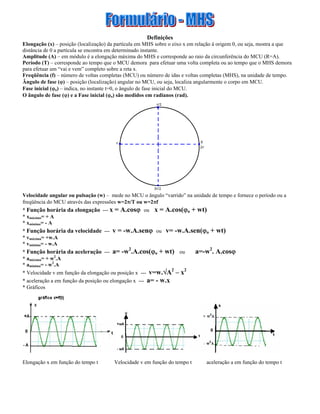
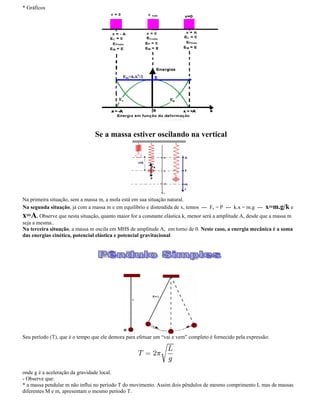
I. O documento apresenta os conceitos fundamentais do movimento harmônico simples, incluindo definições de elongação, amplitude, período, frequência, ângulo de fase, fase inicial e velocidade angular.
II. São descritas as funções horárias da elongação, velocidade e aceleração em termos destas grandezas.
III. Exemplos de exercícios sobre MHS são apresentados para ilustrar a aplicação destes conceitos.