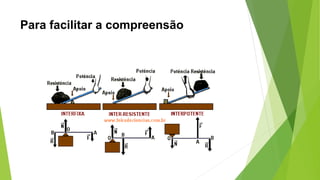
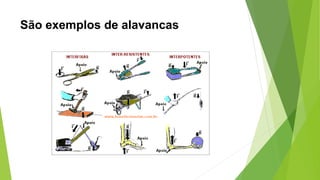
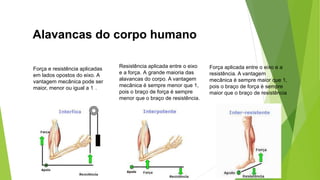
Este documento descreve as máquinas simples, especificamente as alavancas. Explica que as alavancas são classificadas em três tipos - interfixas, inter-resistentes e interpotentes - dependendo da localização do ponto de apoio em relação às forças aplicadas. Também define torque e momento resultante e discute os princípios do equilíbrio estático das alavancas segundo as leis de Newton.