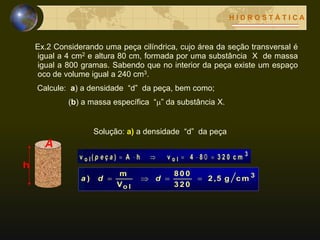
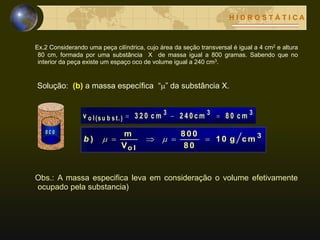
Este documento apresenta os conceitos básicos da hidrostática, que estuda os fluidos em equilíbrio. Os principais conceitos apresentados são: fluido, massa específica, densidade, pressão, pressão hidrostática, pressão absoluta. O documento estrutura a matéria em 4 blocos, abordando os teoremas de Stevin, Pascal e Arquimedes.

1. • a HIDROSTÁTICA estuda os FLUIDOS em equilíbrio.
H I D R O S T Á T I C A
•Professores: Hertz e Jeferson

2. • Considerando
• que o meio em que vivemos é, em
grande parte, composta de ar e água;
H I D R O S T Á T I C A
•Professores: Hertz e Jeferson
• e que nestes meios muitas de nossas atividades se desenvolvem (o
transporte no ar, em rios e mares), foi o que levou o homem estudar
o assunto.

3. • Observemos com atenção !
H I D R O S T Á T I C A
• As bases para estudar esses meios físicos :

4. • Conceitos Básicos:
1. Fluido
2. Massa específica da substância ()
3. Densidade de um corpo (d)
4. Pressão (p)
5. Pressão hidrostática ou efetiva (ph)
6. Pressão absoluta (pabs)
7. Teorema de Stevin
8. Teorema de Pascal
9. Teorema de Arquimedes
H I D R O S T Á T I C A

5. Bloco I
1.Fluido
2.Massa específica da substância ()
3.Densidade de um corpo (d)
H I D R O S T Á T I C A
- Iremos realizar esse estudo em 4 blocos:
Bloco III
7.Teorema de Stevin
8.Teorema de Pasca
Bloco II
4.Pressão (p)
5.Pressão hidrostática ou efetiva (ph)
6.Pressão absoluta (pab)
Bloco IV
8.Teorema de Arquimedes

6. Bloco I
1.Fluido
2.Massa específica da substância ()
3.Densidade de um corpo (d)
H I D R O S T Á T I C A

7. I- Conceitos Básicos:
1. Fluido – estado da matreira no qual a substância
que se encontra naquele estado não apresenta
forma definida. Assim são os líquidos e os gases.
H I D R O S T Á T I C A
São considerados fluidos os líquidos e os gases.
Vol Vol Vol

8. • Conceitos Básicos:
2. Massa específica da substância () – é a medida da razão
entre a massa de uma certa substância homogênea, em
determinada temperatura, e o volume por ela ocupado.
H I D R O S T Á T I C A
volume
massa
: definição
no S I no C G S
3
mk g 3
cmg
Ela é calculada dividindo-se a massa da substancia pelo
volume , efetivamente, por ela ocupado.

9. • Conceitos Básicos:
H I D R O S T Á T I C A
3. Densidade de um corpo (d) – é a razão entre a massa do
corpo, (objeto modelado) em determinada temperatura, e o
volume por ele ocupado.
3
3
3
101
:.
m
k g
cm
g
Obs

volume
massa
d: definição
Ela é calculada dividindo-se a massa do corpo pelo volume ,
total, por ela ocupado.

10. H I D R O S T Á T I C A
Ex.1 Considerando que foram garimpados 800g de um minério, dos quais
600g foram de uma substância X pura e homogênea e que o volume por X
ocupado foi igual a 400 cm3.
Calculando a massa específica (  ) da substância X temos:
3
x
o l
c mg1 ,5
4 0 0
6 0 0
V
m
  x
E x .1S o lu ç ã o

11. H I D R O S T Á T I C A
Ex.2 Considerando uma peça cilíndrica, cujo área da seção transversal é
igual a 4 cm2 e altura 80 cm, formada por uma substância X de massa
igual a 800 gramas. Sabendo que no interior da peça existe um espaço
oco de volume igual a 240 cm3.
Calcule: a) a densidade “d” da peça, bem como;
(b) a massa específica “” da substância X.
3
o lo l c m3 2 084vhA)(v  0p e ç a
3
o l
c mg2 ,5
3 2 0
8 0 0
V
m
)  dda
h
A
Solução: a) a densidade “d” da peça

12. H I D R O S T Á T I C A
Ex.2 Considerando uma peça cilíndrica, cujo área da seção transversal é igual a 4 cm2 e altura
80 cm, formada por uma substância X de massa igual a 800 gramas. Sabendo que no
interior da peça existe um espaço oco de volume igual a 240 cm3.
Solução: (b) a massa específica “” da substância X.
o c o
333
o l(su b s t.) c m8 02 4 0 c mc m3 2 0v 
3
o l
c mg1 0
8 0
800
V
m
)  b
Obs.: A massa especifica leva em consideração o volume efetivamente
ocupado pela substancia)

13. H I D R O S T Á T I C A
Bloco II
4.Pressão (p)
5.Pressão hidrostática ou efetiva (ph)
6.Pressão absoluta (pab)

14. II - Conceitos Básicos:
H I D R O S T Á T I C A
4. Pressão (p) – grandeza que mede a razão entre a intensidade normal de
uma força (FN) por unidade de área (A) onde a força se distribui.
NF

(A )área
A
F
p:definição N (pas cal)Pa
m
N
:te re m osSINo
2

F

NF

HF


15. II - Conceitos Básicos:
H I D R O S T Á T I C A
4. Pressão (p) – grandeza que mede a razão entre a intensidade normal de
uma força (FN) por unidade de área (A) onde a força se distribui.
NF

(A )área
A
F
p:definição N
Obs.: A pressão é uma medida inversamente proporcional a área
de sua atuação.
Obs.: Mantida a força e aumentando-se a área, a pressão
diminuirá proporcionalmente.

16. • Conceitos Básicos:
H I D R O S T Á T I C A
(A )área
NF

Ex. 3 Uma torre de 20 andares tem área da base igual a 850 m2.
Sabendo que a mesma apresenta massa igual a 20 toneladas, e que
também a aceleração da gravidade local é igual a 10 m/s2.
Calcular a pressa exercida na base da torre.
Pa235,3p
850
1020
p
4



E x .3S o lu ç ã o
N1 021 01 02 0gmPe s oF 53
N 


17. H I D R O S T Á T I C A
Ex.4 Um objeto em forma de paralelepípedo de massa 40 kg tem 80cm de
comprimento, 40cm de largura e 20cm de altura. Considerando a
aceleração da gravidade local é igual a 10 m/s2, e que o mesmo
encontra-se apoiada sobre um plano horizontal determine:
a) A área da face ( I )
b) A pressão exercida pela face ( II ) quando esta se encontrar apoiada
no piso, em unidade Pa.
c m8 0
c m4 0
c m2 0
II
III

18. H I D R O S T Á T I C A
a) A área da face ( I )
c m8 0
c m4 0
c m2 0
II
IIIE x .4S o lu ç ã o
2
c m1 6 0 0 2 08 0Aa ) I
Pa32
2
II
105pN/cm0,5
800
400
A
F
p
400N)1040P(Fe)cm8002004(Ab)


b) A pressão exercida pela face ( II ) quando esta se encontrar
apoiada no piso, em unidade Pa.

19. H I D R O S T Á T I C A
5. Pressão hidrostática (efetiva) - em um fluido em equilíbrio o
peso da coluna do fluido gera pressa hidrostática em cada
ponto do fluido.
hgp )B(h  
A
P
hp
P  peso da coluna líquida
A  área da seção transversal
  massa específica do fluido
g  aceleração da gravidade
h  altura da coluna em relação
ao ponto

20. H I D R O S T Á T I C A
6. Pressão absoluta ( pab) - levando-se em conta a pressão
atmosférica (p0) entende-se por pressão absoluta ou total a
soma da pressão hidrostática e a pressão atmosférica:
oab phgp  

21. H I D R O S T Á T I C A
Bloco III
7.Teorema de Stevin
8.Teorema de Pasca
https://pt.wikipedia.org/wiki/Simo
n_Stevin
https://pt.wikipedia.org/wiki/Blaise
_Pascal#/media/Ficheiro:Blaise_
Pascal_2.jpg

22. H I D R O S T Á T I C A
Obs.: Evidência do teorema de Stevin: todos os pontos que se
encontram em uma mesma cota, em um líquido homogêneo e em
equilíbrio, estarão sub uma mesma pressão “superfície
isobárica”.
•07 Teorema de Stevin - III -
“A diferença das pressões entre dois pontos de um fluido, em
equilíbrio, é igual ao produto entre a massa específica do fluido,
a aceleração da gravidade e a o desnível entre os pontos”.

23. H I D R O S T Á T I C A
•Teorema de Stevin - exercícios
01. Um longo tubo de vidro, fechado em sua extremidade superior, é
colocada, mergulhado, nas águas de um lago (μ (água) = 1000 kg/m3) com seu
eixo longitudinal coincidente com a direção vertical, conforme representa a
figura.
No local, a pressão atmosférica vale p = 1,0
atm e g = 10 m/s2. Se o nível da água no
interior do tubo sobe até uma profundidade
h = 5,0 m, medida em relação à superfície
livre do lago, qual é a pressão do ar contido
no interior do tubo?

24. H I D R O S T Á T I C A
•Teorema de Stevin - exercícios
02. A medição da pressão atmosférica reinante no interior de um
laboratório de Física foi realizada utilizando-se o dispositivo representado
na figura:
Sabendo que a pressão exercida
pelo gás, lida no medidor, e de
136 cm Hg, qual então a pressão
atmosférica no local.
03. (UFPE) Se o fluxo sangüíneo não fosse ajustado pela expansão das
artérias, para uma pessoa em pé a diferença de pressão arterial entre o
coração e a cabeça seria de natureza puramente hidrostática. Nesse caso,
para uma pessoa em que a distância entre a cabeça e o coração vale 50
cm, qual o valor em mmHg dessa diferença de pressão? (Considere a
densidade do sangue igual a 103 kg/m3)

25. H I D R O S T Á T I C A
08. O Teorema de Pascal (Blaise Pascal)
“Um acréscimo de pressão comunicado a um ponto qualquer de um líquido
incompressível em equilíbrio transmite-se integralmente a todos os demais pontos do
líquido, bem como às paredes do recipiente.”
O Teorema de Pascal / aplicação
04. Um adestrador quer saber o peso de um
elefante. Utilizando uma prensa hidráulica, consegue
equilibrar o elefante sobre um pistão de 2000 cm2 de
área, exercendo uma força vertical F equivalente a
200 N, de cima para baixo, sobre o outro pistão da
prensa, cuja área é igual a 25 cm2. Calcule o peso do
elefante.

26. H I D R O S T Á T I C A
Bloco IV
8.Teorema de Arquimedes
https://pt.slideshare.net/quero2015/livro-
completo-arquimedes

27. H I D R O S T Á T I C A
09. Teorema de Arquimedes IV
Quando um corpo é imerso total ou
parcialmente em um fluido em equilíbrio, sob a
ação da gravidade, ele recebe do fluido uma
força denominada empuxo (ou impulsão de
Arquimedes).
Tal força tem sempre direção vertical e sentido de baixo para cima e sua
intensidade é igual ao do peso do fluido deslocado pelo corpo.
dFD = densidade do fluido deslocado
g = aceleração da gravidade local
Vol(FD)= volume do flido deslocado

28. H I D R O S T Á T I C A
05. (UFPA) Quando um peixe morre em um aquário, verifica-se que,
imediatamente após a morte, ele permanece no fundo e, após algumas
horas, com a decomposição, são produzidos gases dentro de seu corpo e o
peixe vem à tona (flutua).
A explicação correta para esse fato é que, com a produção de gases:
a) o peso do corpo diminui, diminuindo o empuxo.
b) o volume do corpo aumenta, aumentando o empuxo.
c) o volume do corpo aumenta, diminuindo o empuxo.
d) a densidade do corpo aumenta, aumentando o empuxo.
e) a densidade do corpo aumenta, diminuindo o empuxo

29. H I D R O S T Á T I C A
Teorema de Arquimedes
06. Um balão indeformável de massa 2,0 kg apresenta, num local em que
g =10 m/s2, peso específico de 25 N/m3. Supondo que o balão esteja
totalmente imerso na água (μa 5 1,0 g/cm3), determine:
a) o volume de água deslocado;
b) o módulo do empuxo que o balão recebe da água.
07. Uma esfera de isopor de volume 2,0.102cm3 encontra-se inicialmente
em equilíbrio presa a um fio inextensível, totalmente imersa na agua (fig.1).
Cortando-se o fio, a esfera aflora, passando a flutuar na superficie da agua
(fig. 2).
Sabendo que as massas especificas do
isopor e da agua valem, respectivamente,
0,60 g/cm3 e 1,0 g/cm3 e que |g =10 m/s2,
calcule:
a) a intensidade da força de tração no fio na
situação da fig. 1;
b) a porcentagem do volume da esfera que
permanece imersa na situação da fig. 2.

30. H I D R O S T Á T I C A
Teorema de Arquimedes
08. (Unip-SP) Na figura, as esferas maciças A e B estão ligadas por um
fio ideal e o sistema está em equilíbrio. A esfera A está no interior de um
líquido homogêneo de densidade 2d e a esfera B está no interior de outro
líquido homogêneo de densidade 3d..
09. Um cubo de madeira (densidade = 0,80 g/cm3) de aresta 20 cm flutua
em água (massa específica = 1,0g/cm3) com a face superior paralela à
superfície livre da água. Adotando g 5 10 m/s2, a diferença entre a pressão na
face inferior e a pressão na face superior do cubo é:
a) 1,2 ? 103 Pa. d) 3,0 ? 103 Pa.
b) 1,6 ? 103 Pa. e) 4,0 ? 103 Pa.
c) 2,4 ? 103 Pa.
Sabendo que as esferas têm raios iguais e
que a esfera A tem C densidade d, podemos
concluir que a densidade da esfera B vale:
a) d. b) 2d. c) 3d. d) 4d. e) 5d.