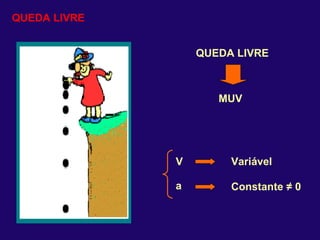
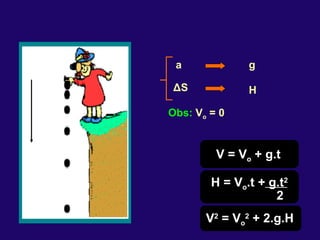
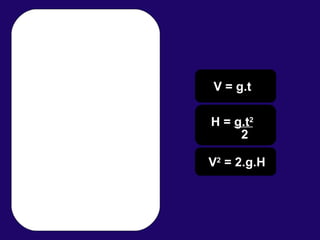
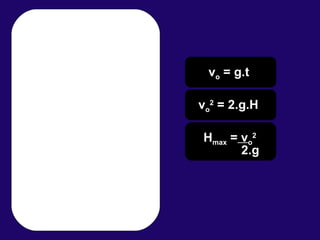
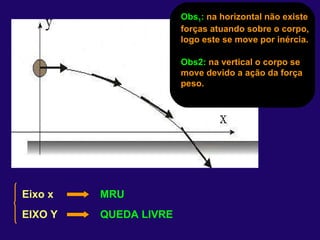
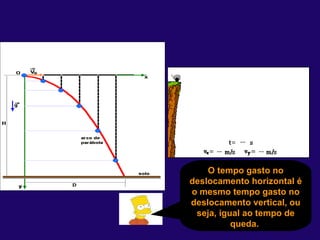
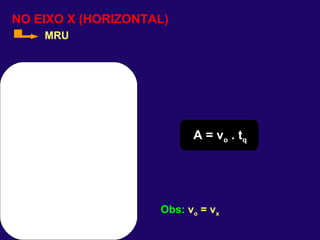
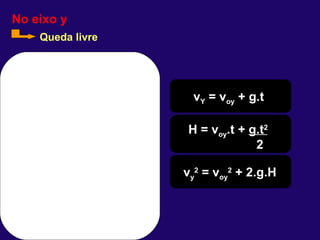
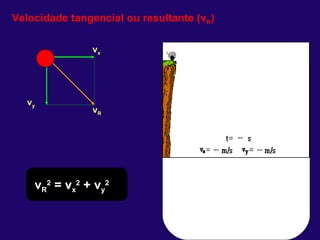
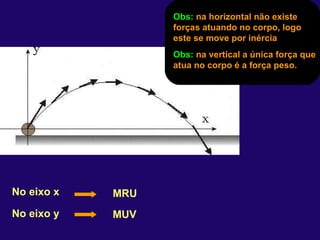
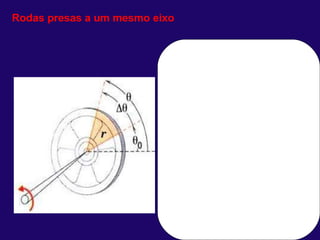
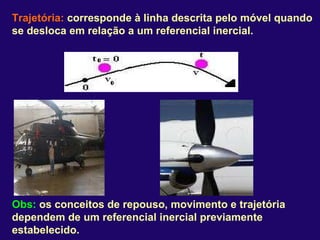
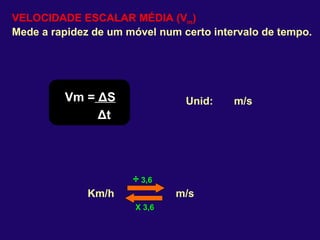
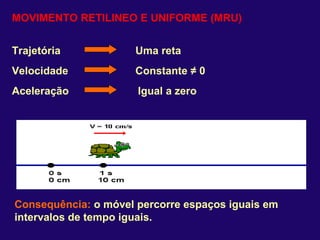
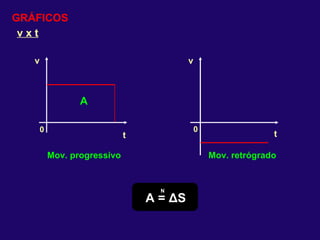
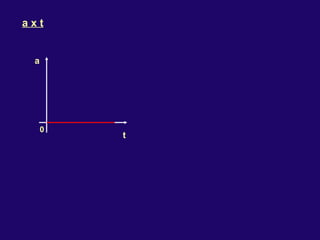
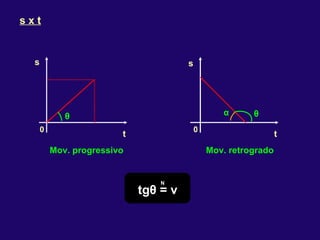
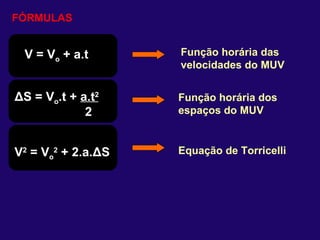
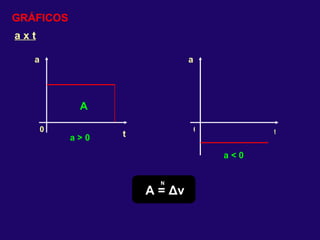
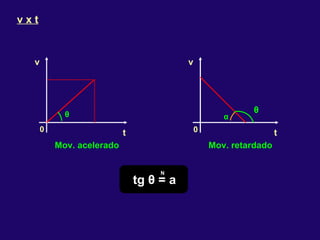
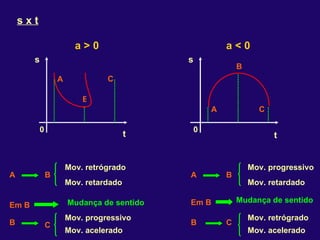
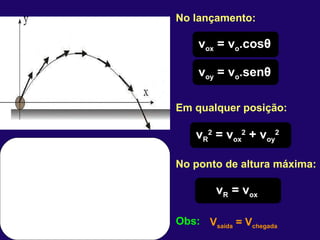
1) O documento discute conceitos fundamentais de cinemática, incluindo posição, deslocamento, velocidade e aceleração de movimentos retilíneos uniformes e uniformemente variados, bem como queda livre e lançamentos vertical e oblíquo. 2) Nos movimentos retilíneos uniformes e uniformemente variados, a aceleração e velocidade podem ser constantes ou variáveis, enquanto a trajetória é uma reta. 3) No lançamento oblíquo, o movimento é retilí

1. CINEMÁTICA GUILHERME

2. Conceito: estuda os movimentos sem se preocupar com suas causas. M.R.U M.R.U.V QUEDA LIVRE LANÇAMENTO VERTICAL PARA CIMA PARA BAIXO LANÇAMENTO HORIZONTAL LANÇAMENTO OBLIQUO MOVIMENTO CIRCULAR

3. CONCEITOS FUNDAMENTAIS Repouso: todo corpo estará em repouso quando sua posição não variar no decorrer do tempo em relação a um referencial inercial adotado. Movimento: todo corpo estará em movimento quando sua posição variar no decorrer do tempo em relação a um referencial inercial adotado.

5. Trajetória: corresponde à linha descrita pelo móvel quando se desloca em relação a um referencial inercial. Obs: os conceitos de repouso, movimento e trajetória dependem de um referencial inercial previamente estabelecido.

7. POSIÇÃO ESCALAR (S) Corresponde à distância que o móvel se encontra em relação a origem. Unid: m (metro) 1 km = 1000 m 1 m = 100 cm 1m = 1000 mm km m cm m X 10 3 ÷ 10 3 ÷ 1O 2 x 10 2 + 0 1 2 3 4 - 1 S (m) S = 2 m S = 4 m Origem dos espaços

8. DESLOCAMENTO ESCALAR ( Δ S) É obtido pela diferença entre a posição final e a posição inicial do móvel. + S (m) 0 1 2 3 4 5 6 - 1 Δ S = S - S O

9. Δ S > 0 Movimento progressivo Δ S < 0 Movimento retrógrado

10. VELOCIDADE ESCALAR MÉDIA (V m ) Mede a rapidez de um móvel num certo intervalo de tempo. Vm = Δ S Δ t Unid: m/s Km/h m/s ÷ 3,6 X 3,6

13. ACELERAÇÃO ESCALAR MÉDIA (a m ) Mede a taxa da variação da velocidade num certo intervalo de tempo. a m = Δ V Δ t Unid: m/s 2 Movimento acelerado: aumento do módulo da velocidade no decorrer do tempo. Movimento retardado: redução do módulo da velocidade no decorrer do tempo.

15. ESTUDO DO SINAL DA ACELERAÇÃO ACELERAÇÃO VELOCIDADE MOVIMENTO + + ACELERADO - - ACELERADO + - RETARDADO - + RETARDADO

16. MOVIMENTO RETILINEO E UNIFORME (MRU) Trajetória Uma reta Velocidade Constante ≠ 0 Aceleração Igual a zero Consequência: o móvel percorre espaços iguais em intervalos de tempo iguais.

17. FÓRMULAS S = So + V.t Função horária dos espaços do MRU _

18. GRÁFICOS v x t v t v t Mov. progressivo Mov. retrógrado A = Δ S 0 0 A N

19. a x t a t 0

20. s x t s t s t Mov. progressivo Mov. retrogrado tg θ = v θ θ 0 0 α N

21. MOVIMENTO RETILINEO UNIFORMEMENTE VARIADO (MRUV) Trajetória Reta Velocidade Variável Aceleração Constante ≠ 0 Consequência: o móvel sofre variações de velocidades iguais em intervalos de tempo iguais.

22. FÓRMULAS V = V o + a.t Δ S = V o .t + a.t 2 2 V 2 = V o 2 + 2.a. Δ S Função horária das velocidades do MUV Função horária dos espaços do MUV Equação de Torricelli

23. GRÁFICOS a x t a t a t A = Δ v a > 0 a < 0 0 0 A N

24. v x t v t v t Mov. acelerado Mov. retardado tg θ = a 0 0 θ α θ N

25. s x t s t s t A B C A B C A B B C A B B C Mov. retrógrado Mov. retardado Mov. progressivo Mov. acelerado Em B Mudança de sentido Mov. progressivo Mov. retardado Mov. retrógrado Mov. acelerado Em B Mudança de sentido 0 0 a > 0 a < 0

26. QUEDA LIVRE QUEDA LIVRE MUV V Variável a Constante ≠ 0

27. a g Δ S H Obs: V o = 0 V = V o + g.t H = V o .t + g.t 2 2 V 2 = V o 2 + 2.g.H

28. V = g.t H = g.t 2 2 V 2 = 2.g.H

29. TEMPO DE QUEDA (t q ) tq = √ 2.H g Consequência: corpos de massas diferentes soltos de uma mesma altura e de um mesmo lugar chegam juntos ao solo.

31. Lançamento vertical Para cima g a - g Δ s H v = v o – g.t H = v o .t – g.t 2 2 V 2 = v o 2 – 2.g.H v = 0 H

32. v o = g.t v o 2 = 2.g.H H max = v o 2 2.g

33. Para baixo g v o V = vo + g.t H = v o .t + g.t 2 2 V 2 = v o 2 + 2.g.H H

34. Lançamento horizontal

35. Eixo x MRU EIXO Y QUEDA LIVRE Obs 1 : na horizontal não existe forças atuando sobre o corpo, logo este se move por inércia. Obs2: na vertical o corpo se move devido a ação da força peso.

36. O tempo gasto no deslocamento horizontal é o mesmo tempo gasto no deslocamento vertical, ou seja, igual ao tempo de queda.

37. NO EIXO X (HORIZONTAL) MRU A = v o . t q Obs: v o = v x

38. No eixo y Queda livre v Y = v oy + g.t H = v oy .t + g.t 2 2 v y 2 = v oy 2 + 2.g.H

39. Velocidade tangencial ou resultante (v R ) v x v y v R v R 2 = v x 2 + v y 2

40. RESUMO DIREÇÃO FORÇAS ATUANDO MOVIMENTO CONSEQUÊNCIAS EIXO X NENHUMA MRU O CORPO PERCORRE ESPAÇOS IGUAIS EM TEMPOS IGUAIS EIXO Y PESO QUEDA LIVRE O CORPO SOFRE VARIAÇÕES DE VELOCIDADES IGUAIS EM TEMPOS IGUAIS

41. Lançamento obliquo

42. No eixo x MRU No eixo y MUV Obs: na vertical a única força que atua no corpo é a força peso. Obs: na horizontal não existe forças atuando no corpo, logo este se move por inércia

43. Analisando as velocidades

44. v ox = v o .cos θ v oy = v o .sen θ v R 2 = v ox 2 + v oy 2 No ponto de altura máxima: v R = v ox No lançamento: Em qualquer posição: Obs: V saída = V chegada

45. No eixo x (horizontal) MRU A = v ox . t t Obs: t t = 2.t s

46. No eixo y (vertical) v y = v oy – g.t H = v oy .t – g.t 2 2 v y 2 = v oy 2 – 2.g.H MUV

47. Equações auxiliares Alcance máximo (A max ) A max = v o 2 sen2 θ g Tempo de subida (ts) T s = v o .sen θ g Obs: o alcance será máximo quando θ = 45 o . Obs: o tempo total de permanência no ar é igual a duas vezes o tempo de subida.

48. Resumo DIREÇÃO FORÇAS ATUANDO MOVIMENTO CONSEQUÊNCIAS EIXO X NENHUMA MRU O CORPO PERCORRE ESPAÇOS IGUAIS EM TEMPOS IGUAIS EIXO Y PESO MUV O CORPO SOFRE VARIAÇÕES DE VELOCIDADES IGUAIS EM TEMPOS IGUAIS

49. Movimento circular e uniforme (MCU) Movimento Velocidade linear (v) Trajetória Circunferência ou um arco de circunferência Constante em módulo Periódico

50. C V 1 V 2 V 3 V 4 | V 1 | = | V 2 | = | V 3 | = | V 4 | Obs: a velocidade é sempre tangente á trajetória.

51. Período (T) Corresponde ao intervalo de tempo de uma volta completa. Frequência (f) Corresponde ao número de voltas na unidade de tempo. Unidade: s Unidade: ciclos p/ segundo = Hz f = 1 T f = n Δ t

52. Deslocamento angular ( Δθ ) Δθ = θ – θ o Unidade: rad π rad = 180 o

54. Relação entre Δθ e Δ s Δθ = R. Δ s

55. Velocidade angular ( ω ) ω = Δθ Δ t Unidade: rad/s ω = 2. π T ω = 2. π . f

56. Relação entre velocidade v e ω v = ω .R v = 2. π .f v = 2. π T

57. Aceleração centrípeta (a cp ) a cp = v 2 R a cp = ω 2 .R

58. Função horária do MCU θ = θ o + ω .t

59. Transmissão de movimento

60. f A .R A = f B .R B R A = R B T A T B Rodas interligadas por uma correia ou corrente

62. Rodas presas a um mesmo eixo