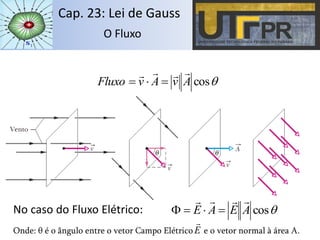
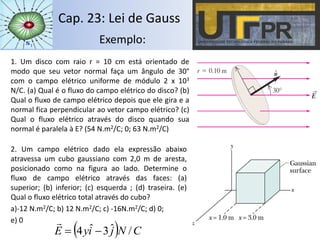
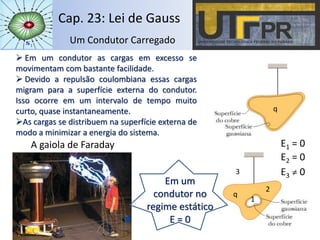
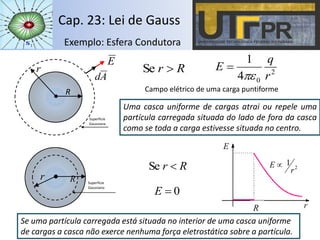
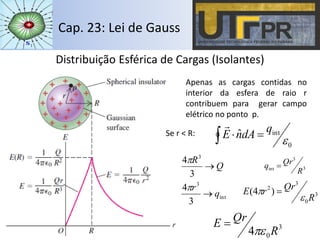
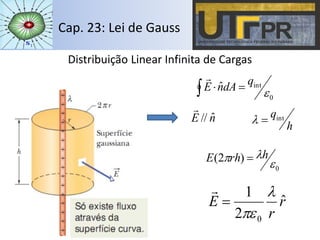
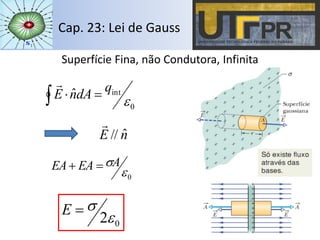
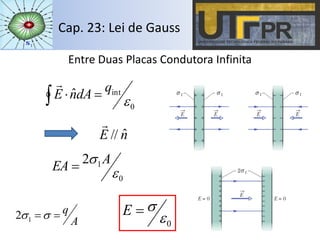
O capítulo descreve a Lei de Gauss, que relaciona o fluxo do campo elétrico através de uma superfície fechada com a carga elétrica contida no interior dessa superfície. A lei é aplicada para distribuições de cargas pontuais, esféricas, cilíndricas, planas e em condutores, calculando o campo elétrico em cada caso. Exemplos ilustram o cálculo do fluxo e campo elétrico para diferentes configurações de cargas.

1. Capítulo 23:
Lei de Gauss

2.  O Fluxo de um Campo Elétrico
 A Lei de Gauss
 A Lei de Gauss e a Lei de Coulomb
 Um Condutor Carregado
 A Lei de Gauss: Simetria Cilíndrica
 A Lei de Gauss: Simetria Plana
 A Lei de Gauss: Simetria Esférica
Cap. 23: Lei de Gauss

3. Cap. 23: Lei de Gauss
Definição
Definição:
A Lei de Gauss considera uma superfície fechada
(imaginária) que envolve a distribuição de cargas.
Essa superfície gaussiana, como é chamada, pode ter
qualquer forma, por isso devemos optar por uma
que facilite o calculo do campo, levando em
consideração as simetrias do problema.

4. Cap. 23: Lei de Gauss
O Fluxo
cosAvAvFluxo


cosAEAE

No caso do Fluxo Elétrico:
Onde: θ é o ângulo entre o vetor Campo Elétrico e o vetor normal à área A.E


5. Cap. 23: Lei de Gauss
O fluxo elétrico através de uma superfície gaussiana
é proporcional ao número de linhas de campo
elétrico que atravessam a superfície.
Definição:
O Fluxo Elétrico
P/ Superfícies
Gaussianas:
  dAnE ˆ

  dAnE ˆ

O vetor Normal, , sempre aponta para fora
da superfície Gaussiana
nˆ

6. Cap. 23: Lei de Gauss
Exemplo:
1. Um disco com raio r = 10 cm está orientado de
modo que seu vetor normal faça um ângulo de 30°
com o campo elétrico uniforme de módulo 2 x 103
N/C. (a) Qual é o fluxo do campo elétrico do disco? (b)
Qual o fluxo de campo elétrico depois que ele gira e a
normal fica perpendicular ao vetor campo elétrico? (c)
Qual o fluxo elétrico através do disco quando sua
normal é paralela à E? (54 N.m2/C; 0; 63 N.m2/C)
2. Um campo elétrico dado ela expressão abaixo
atravessa um cubo gaussiano com 2,0 m de aresta,
posicionado como na figura ao lado. Determine o
fluxo de campo elétrico através das faces: (a)
superior; (b) inferior; (c) esquerda ; (d) traseira. (e)
Qual o fluxo elétrico total através do cubo?
a)-12 N.m2/C; b) 12 N.m2/C; c) -16N.m2/C; d) 0;
e) 0
  CNjiyE /ˆ3ˆ4 


7. Cap. 23: Lei de Gauss
Definição:
0
intˆ

q
dAnE  

A Lei de Gauss relaciona o fluxo do campo elétrico em uma
superfície fechada (Gaussiana) com a carga elétrica contida no
interior dessa superfície.
 O fluxo elétrico não depende da geometria da
superfície fechada, apenas da carga elétrica
contida no seu interior.
Se a carga for positiva, o campo elétrico aponta
para fora da superfície.
 Se a carga for negativa, o campo elétrico
aponta para dentro da superfície.
 O vetor normal à superfície, , sempre aponta
para fora da superfície.
nˆ

8. Cap. 23: Lei de Gauss
Exemplo:
1. Sabendo que q1 = q4 = 3,1 nC, q2 = q5 = - 5,9 nC e q3 =
- 3,1 nC, determine o fluxo do campo elétrico através da
superfície S. (- 670 N.m2/C)
0
intˆ

q
dAnE  

23 – 9. Observa-se experimentalmente que o campo elétrico em uma certa região da
atmosfera terrestre aponta para baixo. A uma altura de 300 m o campo tem módulo de 60
N/C, e a uma altura de 200 m o campo tem módulo de 100 N/C. Determine a carga em
excesso contida em um cubo de 100 m de aresta e faces horizontais a 200 m e 300 m. (3,54
μC)

9. Cap. 23: Lei de Gauss
Obtendo a Lei de Coulomb para uma Carga Pontual
0
intˆ

q
dAnE  

Cuidados na Escolha da Superfície
Gaussiana!
 Escolher uma superfície que envolve a carga
que facilite o calculo da área.
Essa superfície deve conter o ponto no qual o
campo elétrico deve ser determinado.
 Ao longo dessa superfície o campo deve
apresentar uma dependência espacial conhecida
(de preferência constante).
2
int
04
1
r
q
E


0
int2
)4(
 q
rE  r
r
q
E ˆ
4
1
2
int
0



10. Cap. 23: Lei de Gauss
Um Condutor Carregado
 Em um condutor as cargas em excesso se
movimentam com bastante facilidade.
 Devido a repulsão coulombiana essas cargas
migram para a superfície externa do condutor.
Isso ocorre em um intervalo de tempo muito
curto, quase instantaneamente.
As cargas se distribuem na superfície externa de
modo a minimizar a energia do sistema.
q
1
2
q
3
E1 = 0
E2 = 0
E3 ≠ 0
A gaiola de Faraday
Em um
condutor no
regime estático
E = 0

11. Cap. 23: Lei de Gauss
Exemplo: Esfera Condutora
2
04
1
r
q
E


Campo elétrico de uma carga puntiforme
Rr Ser
Superfície
Gaussiana
Ad
E
R
Uma casca uniforme de cargas atrai ou repele uma
partícula carregada situada do lado de fora da casca
como se toda a carga estivesse situada no centro.
Rr Se
0E
r Superfície
Gaussiana
R
2
1
r
E 
R
Se uma partícula carregada está situada no interior de uma casca uniforme
de cargas a casca não exerce nenhuma força eletrostática sobre a partícula.

12. Cap. 23: Lei de Gauss
Distribuição Esférica de Cargas (Isolantes)
Apenas as cargas contidas no
interior da esfera de raio r
contribuem para gerar campo
elétrico no ponto p.
int
3
3
3
4
3
4
q
r
Q
R




0
intˆ

q
dAnE 

3
3
int
R
Qrq 
Se r < R:
3
0
3
2
)4(
R
QrrE

 
3
04 R
QrE



13. Cap. 23: Lei de Gauss
Distribuição Esférica
23.19) Uma esfera condutora uniformemente carregada com
1,2m de diâmetro possui uma densidade de carga superficial
de 8,1 µC/m2. (a) determine a carga da esfera. (b) Determine o
fluxo elétrico através da superfície da esfera. (3,66 x 10-5 C;
4,14x106 Nm2/C)
Duas cascas esféricas concêntricas carregadas tem raios de
10cm e 15cm. A carga da casca menor é 4x10-8 C, e da casca
maior é 2x10-8 C. Determine o campo elétrico (a) em r = 5 cm,
(b) r = 12 cm e (c) r = 20 cm. (0 N/C; 2,5x104 N/C; 1,35x104
N/C)
Exemplos:

14. Cap. 23: Lei de Gauss
Distribuição Esférica
23.51) Na figura uma esfera maciça não-
condutora de raio a a = 2 cm é concêntrica
com uma casca esférica condutora de raio
interno b = 2a e raio externo c = 2,5 a. A
esfera possui um carga q1 = +5 fC e a casca
possui uma carga q2 = -5 fC. Determine o
módulo do campo elétrico (a) em r = 0; (b)
em r = a/2; (c) em r = a; (d) em r =1,5 a; (e)
em r =3,5 a.
(a) 0; b) 5.62x10-2 N/C ;c) 0.112 N/C; d)
0.0499 N/C; e) 0)
Exemplos:

15. Cap. 23: Lei de Gauss
Distribuição Linear Infinita de Cargas
0
intˆ

q
dAnE 

nE ˆ//

h
qint
0
)2(

 hrhE 
r
r
E ˆ
2
1
0





16. Cap. 23: Lei de Gauss
Exemplo: Distribuição Linear de Cargas
Uma casca cilíndrica de comprimento 200m e raio 6cm tem uma
densidade superficial de carga uniforme de 9 nC/m2.(a) Qual a carga
total na casca? Determine o campo elétrico nas seguintes distâncias
radiais do eixo do cilindro. (b) 2 cm; (c) 5,9 cm, (d) 6,1 cm e (e) 10 cm.
(679 nC; 0; 0; 1000 N/C; 610 N/C).
rhA 2
r
r
E ˆ
2
1
0



0
intˆ

q
dAnE 


17. Cap. 23: Lei de Gauss
Superfície Condutora Infinita
0
intˆ

q
dAnE 

nE ˆ//

0
AEA 
0
E

18. Cap. 23: Lei de Gauss
0
intˆ

q
dAnE 

nE ˆ//

0
AEAEA 
02
E
Superfície Fina, não Condutora, Infinita

19. Cap. 23: Lei de Gauss
Entre Duas Placas Condutora Infinita
0
intˆ

q
dAnE 

nE ˆ//

0
12

 A
EA 
0
E
A
q12

20. Cap. 23: Lei de Gauss
Exemplo: Placas Infinitas
A figura mostra partes de duas placas de grande extensão, paralelas, não-
condutoras, ambas com uma carga uniforme dos lados. Os valores das
densidades superficiais de cargas são σ+ = 6,8µC/m2 e σ- = -4,3µC/m2
.Determine o campo elétrico (a) à esquerda; (b) entre e (c) à direita das
placas. (1,4x105 N/C; 6,3x105 N/C)

21. Cap. 23: Lei de Gauss
Lista de Exercícios
1, 3, 6, 7, 12, 13, 15, 19, 21, 25,
27, 31, 39, 41, 43, 49, 51, 53, 57, 81
Referências
HALLIDAY, D.; RESNICK, R.; WALKER, J.; Fundamentos de Física:
Eletromagnetismo. 8a ed. Rio de janeiro: LTC, 2009. v3.
TIPLER, P. A.; Física para Cientistas e Engenheiros. 4a ed, LTC, 2000. v2.
SEARS, F.; ZEMANSKY, M.W.; YOUNG, H.; FREEDMAN, R.A.; Física:
Eletromagnetismo. 12a ed. São Paulo: Pearson Addison Wesley, 2008. v3.