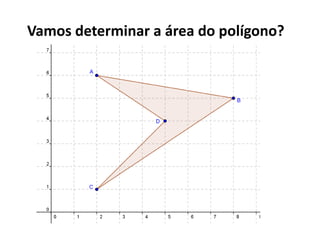
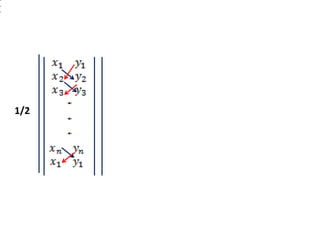
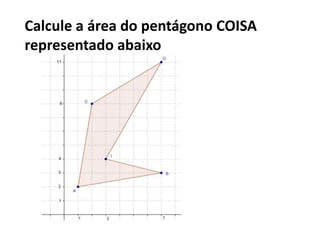
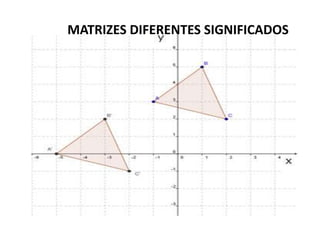
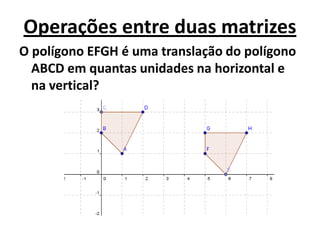
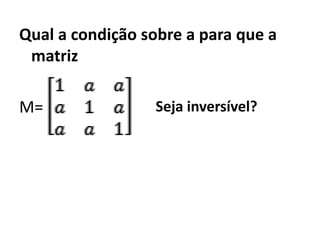
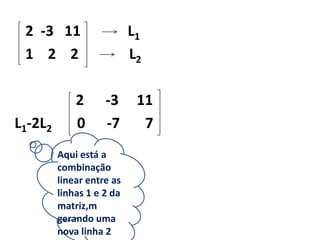
1) O documento discute matrizes, determinantes e sistemas lineares, apresentando conceitos e exemplos destes tópicos da álgebra linear.
2) É apresentada uma citação de Paulo Freire sobre a importância da educação para a transformação da sociedade.
3) São mostrados exemplos de cálculo de determinantes utilizando a regra de Sarrus e propriedades dos determinantes.



































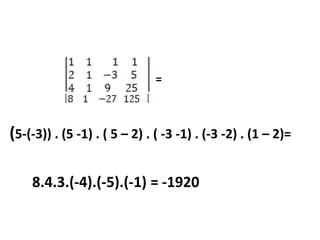














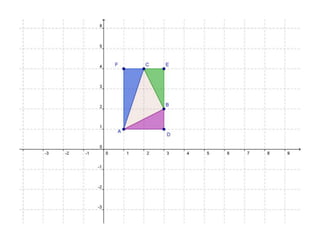

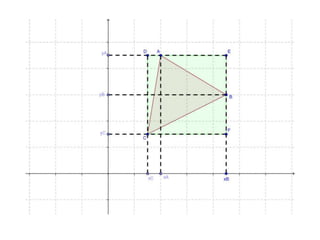
![Área(DEFC)= (xB - xC).(yA- yC)Área(BFC) = [(xB - xC).(yB- yC)]/2Área(ABE) = [(xB - xA).(yA- yB)]/2Área(ADC) = [(xA- xC).(yA- yC)]/2Área do triângulo ABC= (xB - xC).(yA- yC)-{[(xB - xC).(yB- yC)]/2 + [(xB - xA).(yA- yB)]/2 + [(xA- xC).(yA- yC)]/2}Área do ABC = [xA.yB+xC.yA+xB.yC-(xC.yB+xA.yC+xB.yA)]/2](https://image.slidesharecdn.com/implementao-md4-encontro1-110905125943-phpapp01/85/Implementacao-mod4-61-320.jpg)
![Por determinante½xA.yB+xC.yA+xB.yC-(xC.yB+xA.yC+xB.yA)]/2](https://image.slidesharecdn.com/implementao-md4-encontro1-110905125943-phpapp01/85/Implementacao-mod4-62-320.jpg)