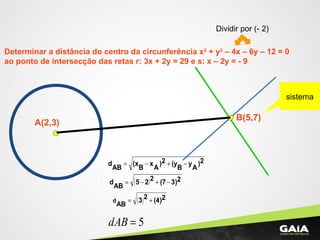
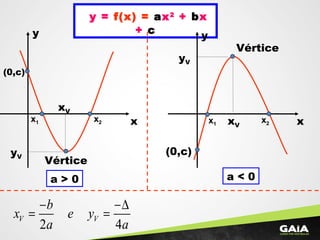
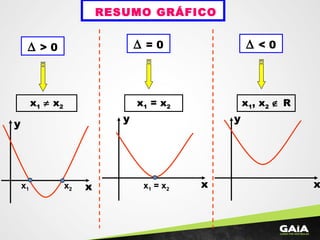
1) O documento apresenta conceitos sobre logaritmos, incluindo suas propriedades e casos particulares. 2) É resolvida uma equação com logaritmos, chegando-se à solução x = 5. 3) Há resumos sobre gráficos de funções quadráticas e sobre multiplicação e determinantes de matrizes.

1. PROFESSOR RICARDINHO

2. logB A = x ↔ A = Bx
CASOS PARTICULARESCASOS PARTICULARES
logB 1 = 0 logA A = 1
PROPRIEDADESPROPRIEDADES
logC (A.B) = logc A + logc B
logC (A/B) = logc A – logc B
logA Am
= m
Logaritmos....Logaritmos....
A > 0 1 ≠ B > 0
logC Am
= m.logc A

3. A solução da equação loglog22 (x + 4) + log(x + 4) + log22(x – 3) = log(x – 3) = log221818, é:
loglog22 (x + 4) + log(x + 4) + log22(x – 3) = log(x – 3) = log221818 loga
(b . c) = loga
b + loga
c
loglog22 (x + 4).(x – 3) = log(x + 4).(x – 3) = log221818
loglog22 (x + 4).(x – 3) = log(x + 4).(x – 3) = log221818
(x + 4).(x – 3) = 18
x2
– 3x + 4x – 12 = 18
x2
+ x – 12 – 18 = 0
x2
+ x – 30 = 0
x2
+ x – 30 = 0
a = 1 b = 1 c = - 30
∆ = b2
– 4ac
∆ = 12
– 4.1.(-30)
∆ = 1 + 120
∆ = 121
2
111-
x
2a
b
x
±
=
∆±−
=
Logo temos: x = 5

4. y = f(x) = ax2
+ bx
+ c
Vértice
(0,c)
xV
yV
x1 x2
Vértice
(0,c)
xV
yV
x1
x2
y
x x
y
a > 0 a < 0
2 4
V V
b
x e y
a a
− −∆
= =

5. RESUMO GRÁFICO
∆ > 0
x1 ≠ x2
x1 x2
y
x
∆ = 0
x1 = x2
x1 = x2
x
y
∆ < 0
x1, x2 ∉ R
x
y

6. MULTIPLICAÇÃO DE MATRIZES
pxmpxnnxm CB.A =
nn =
535223
. xxx
CBA =
Na multiplicação de matrizes não vale a lei do anulamento, ou seja
podemos ter A.B = 0 mesmo com A ≠ 0 B ≠ 0.
.
00
11






=





−10
10 0 0
0 0






MATRIZES/DETERMINANTES
det A- 1
= 1
det A
Se det A = 0
Não existe inversa
(A é singular)
A.A-1
= I
Se det A ≠ 0 Existe inversa
(A é inversível)
MATRIZ INVERSA

7. NÃO ESQUECER!!!!!!
det(A.B) = detA.det B (Teorema de Binet)
CUIDADO: det(A + B) ≠ detA + det B
vale lembrar que:vale lembrar que:
det (k.A) = kn
. det A
k ∈ R, n é a ordem da matriz

8. Determinar a distância do centro da circunferência x2
+ y2
– 4x – 6y – 12 = 0
ao ponto de intersecção das retas r: 3x + 2y = 29 e s: x – 2y = - 9
A(2,3)
Dividir por (- 2)
B(5,7)
sistema
2)
A
y
B
(y2)
A
x
B
(x
AB
d −+−=
( ) 23)(7225
AB
d −+−=
( ) 2(4)23
AB
d +=
5=dAB