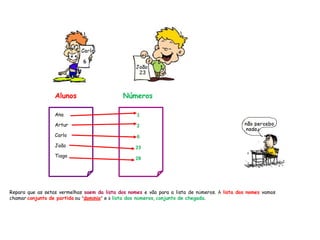
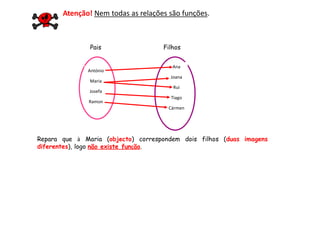
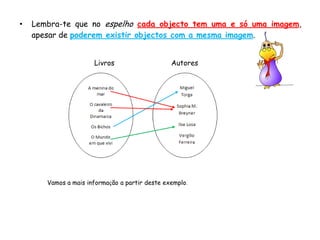
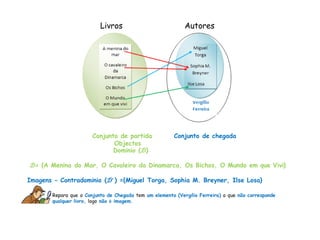
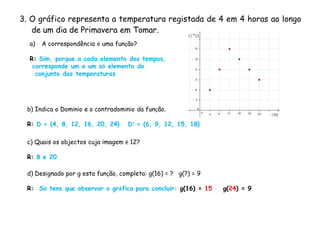
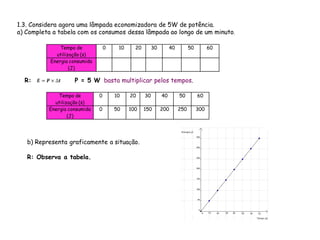
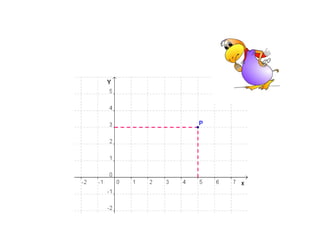
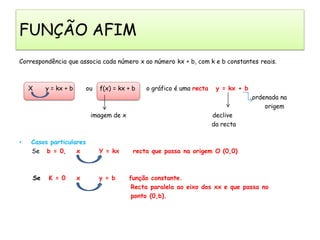
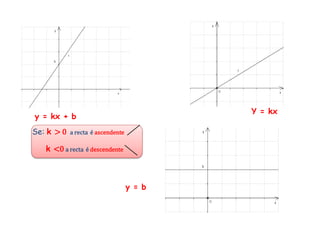
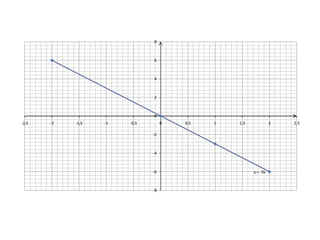
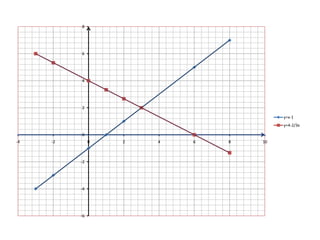
O documento descreve as características de uma função matemática. Explica que uma função é uma relação "bem comportada" onde cada elemento do conjunto de partida (domínio) está associado a um único elemento do conjunto de chegada (contradomínio). Fornece exemplos de relações que são funções e relações que não o são.

2. • No quotidiano temos muitas relações, basta pensares na tua turma.
Os nomes e os números. Os teus vizinhos, moradas e números de
porta. Por vezes “ordenamos”. Pensa, o nome dos teus colegas e os
números na sala de aula, isto significa que um vem antes e outro
depois. Podíamos estabelecer essa relação.
• Uma função é uma relação "bem comportada", tal como os
membros de uma família, uns são mais bem comportados do que
outros. (Atenção:.. Isto significa que, apesar de todas as funções
serem relações, nem todas as relações são funções. Quando
dizemos que a função é "uma relação bem comportada ", significa
que, dado um ponto de partida, sabemos exactamente para onde ir,
dado um x(nome), temos um e um só y(número).

3. Alunos Números
Ana 1
Artur 2
Carlo 6
João 23
Tiago
28
Repara que as setas vermelhas saem da lista dos nomes e vão para a lista de números. À lista dos nomes vamos
chamar conjunto de partida ou “domínio” e à lista dos números, conjunto de chegada.

4. O domínio é onde se começa.
Agora vamos pensar num espelho.
Temos um objecto e temos uma só imagem
Nestes casos temos uma função.
Aqui aparece o termo “imagem”, porque a vemos.
No caso da relação “Alunos - Números” também podemos dizer que os Alunos são os
objectos e os Números as imagens, e também temos uma função.

5. Atenção! Nem todas as relações são funções.
Pais Filhos
Ana
António
Joana
Maria
Rui
Josefa
Tiago
Ramon
Cármen
Repara que à Maria (objecto) correspondem dois filhos (duas imagens
diferentes), logo não existe função.

6. • Lembra-te que no espelho cada objecto tem uma e só uma imagem,
apesar de poderem existir objectos com a mesma imagem.
Livros Autores
Vamos a mais informação a partir deste exemplo.

7. Livros Autores
Conjunto de partida Conjunto de chegada
Objectos
Domínio (D)
D= {A Menina do Mar, O Cavaleiro da Dinamarca, Os Bichos, O Mundo em que Vivi}
Imagens – Contradomínio (D’ ) ={Miguel Torga, Sophia M. Breyner, Ilse Losa}
Repara que o Conjunto de Chegada tem um elemento (Vergílio Ferreira) a que não corresponde
qualquer livro, logo não é imagem.

8. Exemplos.
1. Considera a seguinte correspondência entre os conjuntos A e B.
A – conjunto de partida B – conjunto de chegada
Df = {4, 8, 11} D ‘f = {8, 16, 22}
Em linguagem corrente podemos dizer:
“ao 4 corresponde o 8”
escrevendo com símbolos matemáticos:
lemos: “ de 4 é igual a 8”
Se observarmos a correspondência, verificamos que a cada valor do conjunto A corresponde o dobro
em B. Podemos escrever a expressão analítica do que observamos:

9. 1. A tabela seguinte apresenta a correspondência
entre um número e o seu quadrado
Número 0 1 2 3 4
Quadrado do número 0 1 4 9 16
a) Justifica que a tabela representa uma função.
R: A tabela representa uma função porque a cada número corresponde um e
um só quadrado do número.
b) Indica o domínio e o contradomínio da função.
R: D = {0; 1; 2; 3; 4}
D’ = {0; 1; 4; 9; 16}
c) Qual a imagem de 2? Qual é a imagem de 4?
R: A imagem de 2 é 4.
A imagem de 4 é 16
d) Qual é o objecto que tem por imagem 9?
R: O objecto que tem por imagem 9 é o 3.

10. 2. A tabela seguinte mostra a distância que um automóvel percorre até se
imobilizar segundo a velocidade a que seguia
Velocidade (km/h) 60 90 120 150 180
Distância de paragem (m) 34. 64. 104. 152. 209.
4 9 2 4 4
a) A tabela representa uma função? Justifica a resposta.
R: Sim, porque a cada velocidade corresponde uma e só uma distância.
b) Qual é a imagem de 90 km/h? E qual é o objecto que tem por imagem 209,4 m?
R: 64,9 m. 180 km/h
c) Para que o automóvel pare antes de bater num obstáculo a 100 m, o condutor pode
circular a 120 km/h?
R: Não, porque necessita de 104,2 m para parar e só tem 100 m.

11. 3. O gráfico representa a temperatura registada de 4 em 4 horas ao longo
de um dia de Primavera em Tomar.
a) A correspondência é uma função?
R: Sim, porque a cada elemento dos tempos,
corresponde um e um só elemento do
conjunto das temperaturas
b) Indica o Domínio e o contradomínio da função.
R: D = {4, 8, 12, 16, 20, 24} D’ = {6, 9, 12, 15, 18}
c) Quais os objectos cuja imagem é 12?
R: 8 e 20
d) Designado por g esta função, completa: g(16) = ? g(?) = 9
R: Só tens que observar o gráfico para concluir: g(16) = 15 g(24) = 9

12. 4. A energia consumida é calculada conhecendo a potência utilizada e o
tempo decorrido:
Unidades SI
E Energia consumida joule (J)
Intervalo de tempo segundo (s)
P Potência watt (W)
1.1. Calcula a energia consumida por uma máquina e lavar roupa com 2100 W de potência que
funcionou durante uma hora.
R: Deves reparar que o intervalo de tempo está em segundos e o tempo
de funcionamento da máquina foi de 1 hora pelo que tens que reduzir horas a segundos.
1h = 3600 s então:
1.2. Determina a energia consumida durante 30 minutos, por uma lâmpada de 40 w.
R: 30 min = 1800 s

13. 1.3. Considera agora uma lâmpada economizadora de 5W de potência.
a) Completa a tabela com os consumos dessa lâmpada ao longo de um minuto.
Tempo de 0 10 20 30 40 50 60
utilização (s)
Energia consumida
(J)
R: P = 5 W basta multiplicar pelos tempos.
Tempo de 0 10 20 30 40 50 60
utilização (s)
Energia consumida 0 50 100 150 200 250 300
(J)
b) Representa graficamente a situação.
R: Observa a tabela.

14. c) Quanto tempo esteve a lâmpada acesa para ter um consumo de 900 J?
R: Podes utilizar o gráfico ou a tabela para resolver a questão ou então através
da fórmula , mas agora o que se pretende é ,
então convertendo em minutos teremos
3 min.

15. Coordenadas de um ponto no plano
• Consideremos no plano um sistema de eixos coordenados.
• Qualquer ponto P do plano, pode caracterizar-se pelos números, x e y, que são as
projecções do ponto sobre os eixos.
• Então o ponto P, tem coordenadas (x, y), ou seja, x é a abcissa e y é a ordenada.
• Por exemplo se um ponto P tem como coordenadas (5,3), andamos 5 unidades no eixo
dos x e 3 unidades no eixo dos y. clicar

17. FUNÇÃO AFIM
Correspondência que associa cada número x ao número kx + b, com k e b constantes reais.
X y = kx + b ou f(x) = kx + b o gráfico é uma recta y = kx + b
ordenada na
origem
imagem de x declive
da recta
• Casos particulares
Se b = 0, x Y = kx recta que passa na origem O (0,0)
Se K = 0 x y = b função constante.
Recta paralela ao eixo dos xx e que passa no
ponto (0,b).

18. Y = kx
y = kx + b
Se: k > 0 a recta é ascendente
k <0 a recta é descendente
y = b

19. EXEMPLOS
1. Vamos começar com as funções de proporcionalidade directa, do tipo , lembra-te que
as funções de proporcionalidade directa são representadas por rectas que passam na origem
(0,0)
• Representa graficamente a função
R: Vamos fazer uma tabela dando valores a x e obter os respectivos valores de y.
x y
-2 -3(-2) = 6 agora traçamos o gráfico
0 -3(0) = 0
1 -3(1) = -3
2 -3(2) = -6

20. 8
6
4
2
0
-2,5 -2 -1,5 -1 -0,5 0 0,5 1 1,5 2 2,5
-2
-4
-6 y = -3x
-8

21. 2. Traçar os gráficos das funções: e
R: Temos que fazer duas tabelas independentes, uma para cada função.
x y x y
-3 -4
-3 6
-2 -3
-2 5,333333
0 -1
0 4
1 0
1 3,333333
2 1
2 2,666667
3 2
3 2
6 5
6 0
8 7
8 -1,33333
gráfico

22. 8
6
4
2
y=x-1
y=4-2/3x
0
-4 -2 0 2 4 6 8 10
-2
-4
-6

23. Acabou, por agora!...
Vamos ao trabalho se não
Já sabem o que acontece!…
Janeiro 2011
O professor: Carlos Jaime Q. Lopes