1) O documento descreve conceitos de funções algébricas, incluindo zeros no denominador, retas assintotas verticais e inclinadas, e comportamento do gráfico quando x tende a valores extremos. 2) Dois exemplos são resolvidos graficamente para ilustrar esses conceitos, incluindo detectar retas assintotas e analisar variação, concavidades e comportamento no infinito. 3) O documento introduz o conceito de retas assintotas inclinadas, discutindo como determinar seus coeficientes

1. Aula 7
Esbo»ando gr¶¯cos: zeros no
c a
denominador e retas ass¶
³ntotas
³nuas em R, com derivadas
Na aula 6, estivemos concentrados no estudo de fun»~es cont¶
co
primeira e segunda tamb¶m cont¶
e ³nuas.
Nesta aula, estaremos voltando nossa aten»~o para fun»~es alg¶bricas. Uma fun»~o
ca co e ca
¶ alg¶brica quando sua f¶rmula f (x) envolve todas ou algumas das quatro opera»oes
e e o p c~
racionais +, ¡, £ e ¥, e eventualmente extra»~es de ra¶ n-¶simas (
co ³zes e n
).
Na verdade, as fun»~es da aula 6 s~o tamb¶m fun»oes alg¶bricas.
co a e c~ e
As fun»~es alg¶bricas que estaremos estudando agora, por¶m, tem uma ou v¶rias das
co e e a
seguintes peculiaridades:
(i) o denominador na f¶rmula de f (x) se anula para um ou mais valores de x;
o
e ³nua em x, mas f 0 n~o o ¶;
(ii) para alguns valores de x, f ¶ cont¶ a e
(iii) para alguns valores de x, f e f 0 s~o cont¶
a ³nuas em x, mas f 00 n~o o ¶;
a e
(iv) quando x ! +1 (ou quando x ! ¡1), a curva y = f(x) aproxima-se
inde¯nidamente de uma reta (chamada reta ass¶ ³ntota da curva y = f(x)). (Os
gr¶¯cos das fun»oes dos problemas 4 e 6, p¶gina 55, tem ass¶
a c~ a ³ntotas horizontais).
A apresenta»~o desses novos aspectos no esbo»o de gr¶¯cos de fun»~es ser¶ feita
ca c a co a
atrav¶s de exemplos. Vamos a eles.
e
2x + 1
Exemplo 7.1 Esbo»ar o gr¶¯co de f , sendo f (x) =
c a , ou seja, esbo»ar a curva
c
x¡2
2x + 1
y= .
x¡2
Detectando ass¶
³ntotas verticais
Repare que D(f ) = R ¡ f2g.
57

2. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 58
5 5
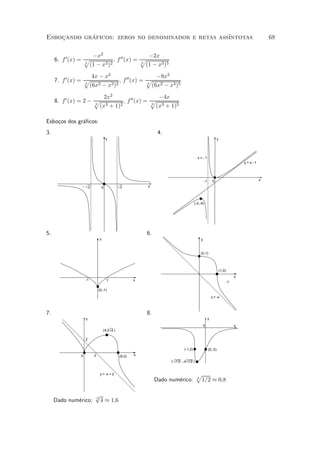
Agora, lim f (x) = lim = = +1, e lim f (x) = lim = ¡ = ¡1
+
x!2 x!2
x>2
0+ x!2 ¡ x!2
x<2
0
Esses limites laterais, sendo in¯nitos, detectam que a reta vertical de equa»~o ca
x = 2 ¶ uma ass¶
e ³ntota vertical do gr¶¯co de f. Mais precisamente, esses limites laterais
a
detectam que
quando x ! 2+ , os pontos correspondentes, no gr¶¯co, sobem" no plano xy, aproxi-
a
mando-se inde¯nidamente dessa reta. Quando x ! 2¡ , os pontos do gr¶¯co descem"
a
no plano xy, tamb¶m aproximando-se inde¯nidamente da reta ass¶
e ³ntota.
Crescimento e decrescimento
Temos
(2x + 1)0 (x ¡ 2) ¡ (x ¡ 2)0 (2x + 1) 2(x ¡ 2) ¡ (2x + 1)
f 0 (x) = =
(x ¡ 2) 2 (x ¡ 2)2
Portanto
¡5
f 0 (x) =
(x ¡ 2)2
Assim sendo f 0 (x) < 0 para todo x em D(f ) = R ¡ f2g. Esta fun»~o f n~o pode ter
ca a
m¶ximos nem m¶
a ³nimos locais.
Temos o seguinte diagrama de sinais de f 0 e intervalos de crescimento e decresci-
mento de f :
f' _ 2 _ x
f ∃ f(2)
Concavidades do gr¶¯co
a
Temos
· ¸0
00 ¡5
f (x) = = [¡5(x ¡ 2)¡2 ]0 = 10(x ¡ 2)¡3
(x ¡ 2)2
Temos o seguinte diagrama de sinais de f 00 e dire»~es de concavidades do gr¶¯co de f :
co a
f '' _ 2 +
y = f(x) x
Como 2 6
2 D(f ), o gr¶¯co n~o tem ponto de in°ex~o.
a a a
Comportamento no in¯nito (outras ass¶
³ntotas)
2x + 1
lim f(x) = lim =2
x!+1 x!+1 x ¡ 2

3. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 59
Tamb¶m lim f (x) = 2
e
x!¡1
Assim, a reta y = 2 ¶ uma ass¶
e ³ntota horizontal µ direita e µ esquerda do gr¶¯co
a a a
de f .
Esbo»o do gr¶¯co de f , com base nos aspectos estudados acima: ¯gura 7.1
c a
8
6
4
y=2 2
0 2 4 6 8
-4 -2
-2 x=2
-4
Figura 7.1.
x2 ¡ 2x + 2
Exemplo 7.2 Esbo»ar o gr¶¯co de y =
c a .
x¡1
Detectando ass¶
³ntotas verticais
Repare que D(f ) = R ¡ f1g.
x2 ¡ 2x + 2 1 x2 ¡ 2x + 2 1
Agora, lim = + = +1, e lim = ¡ = ¡1
x!1 + x¡1 0 x!1¡ x¡1 0
A reta vertical de equa»~o x = 1 ¶ uma ass¶
ca e ³ntota vertical do gr¶¯co da curva
a
2
y = x ¡2x+2 .
x¡1
Quando x est¶ pr¶ximo de 1, pontos da curva sobem" no plano xy, aproximando-
a o
se da ass¶
³ntota, µ direita, e descem", aproximando-se da ass¶
a ³ntota, µ esquerda.
a
Crescimento e decrescimento. M¶ximos e m¶
a ³nimos locais
Temos
(x2 + 2x + 2)0 (x ¡ 1) ¡ (x ¡ 1)0 (x2 + 2x + 2)
y0 =
(x ¡ 1)2
(2x ¡ 2)(x ¡ 1) ¡ (x2 ¡ 2x + 2) x2 ¡ 2x
= =
(x ¡ 1)2 (x ¡ 1)2

4. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 60
Portanto
x2 ¡ 2x x(x ¡ 2)
y0 = =
(x ¡ 1)2 (x ¡ 1)2
Assim, y 0 = 0 para x = 0 e para x = 2.
As ra¶ do numerador de y 0 s~o 0 e 2, enquanto que 1 ¶ raiz do denominador.
³zes a e
Al¶m disso, em cada um dos intervalos ]¡ 1; 0[, ]0; 1[, ]1; 2[ e ]2; +1[, a derivada y 0
e
mant¶m-se positiva ou negativa.
e
Este fato nos ¶ garantido por um teorema da An¶lise Matem¶tica, chamado teo-
e a a
rema do anulamento, ou teorema de Bolzano, que enuncia
Teorema de Bolzano Se uma fun»~o cont¶
ca ³nua f n~o tem ra¶ em um intervalo,
a ³zes
ent~o f (x) mant¶m-se positiva ou negativa em todos os pontos x do intervalo.
a e
Com base nessas observa»~es, para analisar a varia»~o de sinais de y 0 podemos
co ca
recorrer ao seguinte argumento:
Quando x ¶ muito grande, y 0 > 0. Assim, y 0 > 0 no intervalo x > 2. Quando x passa
e
por 2, y 0 troca de sinal. Portanto, y 0 < 0 para 1 < x < 2. Quando x passa por 1, y 0
n~o muda de sinal porque o termo x¡ 1 aparece elevado ao quadrado no denominador.
a
Assim sendo, temos ainda y 0 < 0 no intervalo 0 < x < 1. Ao passar por 0, y 0 troca
de sinal novamente e temos ent~o y 0 > 0 quando x < 0.
a
Temos ent~o o seguinte diagrama de sinais de y 0 e intervalos de crescimento e
a
decrescimento de y:
y' + 0 _ 1 _ 2 + x
y pto de ∃ y(1) pto de
max min
local local
y' = 0 y' = 0
Temos ent~o que y cresce em ]¡ 1; 0], decresce em [0; 1[ e em ]1; 2], e cresce em
a
[2; +1[.
Concavidades e in°ex~es do gr¶¯co
o a
Temos
· ¸0
00x2 ¡ 2x (x2 ¡ 2x)0 (x ¡ 1)2 ¡ [(x ¡ 1)2 ]0 (x2 ¡ 2x)
y = =
(x ¡ 1)2 (x ¡ 1)4
(2x ¡ 2)(x ¡ 1)2 ¡ 2(x ¡ 1)(x2 ¡ 2x)
=
(x ¡ 1)4
(2x ¡ 2)(x ¡ 1) ¡ 2(x2 ¡ 2x) 2
= =
(x ¡ 1)3 (x ¡ 1)3

5. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 61
y'' _ 1 +
y = y(x) x
Temos o seguinte diagrama de sinais de y 00 e dire»oes de concavidades da curva y = y(x):
c~
Como n~o h¶ y para x = 1, o gr¶¯co n~o tem ponto de in°ex~o.
a a a a a
Comportamento no in¯nito (outras ass¶
³ntotas)
x2 ¡ 2x + 2 x2
lim y(x) = lim = lim = lim x = +1
x!+1 x!+1 x¡1 x!+1 x x!+1
x2
Temos ainda lim y(x) = lim = lim x = ¡1
x!¡1 x!¡1 x x!¡1
Assim, a curva n~o tem ass¶
a ³ntota horizontal.
Esbo»o do gr¶¯co de f , com base nos elementos coletados acima: ¯gura 7.2
c a
y
4
3
2
1
0 1 2 3 x
-4 -2
-1 x=1
-2
-3
Figura 7.2.
Ass¶
³ntotas inclinadas!
H¶ algo mais que pode ser destacado no gr¶¯co esbo»ado na ¯gura 7.2: a exis-
a a c
t^ncia, at¶ aqui insuspeita, de uma ass¶
e e ³ntota inclinada (tamb¶m chamada ass¶
e ³ntota
obl¶
³qua).
Se lim [f (x) ¡ (ax + b)] = 0, para certos n¶meros reais a e b, temos que a reta
u
x!+1
y = ax + b ¶ uma ass¶
e ³ntota do gr¶¯co de f µ direita, uma ass¶
a a ³ntota inclinada se a 60.
=

6. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 62
Neste caso, µ medida em que x cresce, tornando-se muito grande, com valores
a
positivos, f(x) torna-se cada vez mais pr¶ximo de ax + b.
o
Por raz~es an¶logas, a reta y = ax+b ¶ uma ass¶
o a e ³ntota do gr¶¯co de f , µ esquerda,
a a
quando lim [f (x) ¡ (ax + b)] = 0.
x!¡1
Como determinar os coe¯cientes a e b ?
Para determinar a, note que se lim [f(x) ¡ (ax + b)] = 0, ent~o
a
x!§1
f (x) [f (x) ¡ (ax + b)] + (ax + b)
lim = lim
x!§1 x x!§1 x
f (x) ¡ (ax + b) ax + b
= lim + lim
x!§1 x x!§1 x
0
= +a=a
+1
Assim, se a reta y = ax + b ¶ uma ass¶
e ³ntota do gr¶¯co de f ent~o
a a
f (x) f(x)
lim = a ou lim =a
x!+1 x x!¡1 x
Para determinar b, basta agora calcularmos
lim (f (x) ¡ ax) = b
x!§1
No caso da curva que estamos estudando,
f (x) y x2 ¡ 2x + 2
lim = lim = lim
x!§1 x x!§1 x x!§1 x(x ¡ 1)
2
x ¡ 2x + 2 x2
= lim = lim 2 = 1
x!§1 x2 ¡ x x!§1 x
e assim obtemos a = 1.
Al¶m disso,
e
µ ¶ µ ¶
x2 ¡ 2x + 2 x2 ¡ 2x + 2
lim ¡ ax = lim ¡x
x!§1 x¡1 x!§1 x¡1
x2 ¡ 2x + 2 ¡ x(x ¡ 1)
= lim
x!§1 x¡1
¡x + 2
= lim = ¡1
x!§1 x ¡ 1
e assim obtemos b = ¡1.
Portanto, a reta y = x ¡ 1 ¶ ass¶
e ³ntota inclinada da curva.
Com base nos elementos coletados acima, incluindo a informa»~o adicional sobre
ca
a ass¶
³ntota inclinada, temos um novo esbo»o, mais preciso, da curva da ¯gura 7.2, na
c
¯gura 7.3.

7. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 63
y
4
3
2
y= x-1
1
0 1 2 3 x
-4 -2
-1 x=1
-2
-3
Figura 7.3.
p
Exemplo 7.3 Esbo»ar o gr¶¯co de y = f(x) = (x + 2) 3 (x ¡ 3)2 .
c a
O gr¶¯co desta fun»~o f n~o apresenta ass¶
a ca a ³ntotas verticais, visto que a fun»~o f
ca
e ³nua em todo o conjunto R, isto ¶, em todos os pontos de R.
¶ cont¶ e
Crescimento e decrescimento. M¶ximos e m¶
a ³nimos locais
p
Temos y = (x + 2) 3 (x ¡ 3)2 .
Para calcular y 0 , primeiro faremos
y = (x + 2)(x ¡ 3)2=3
Desse modo, pela regra da derivada de um produto,
2
y 0 = (x ¡ 3)2=3 + (x + 2) ¢ (x ¡ 3)¡1=3
3
Agora, para facilitar os c¶lculos, colocamos em evid^ncia a fra»~o 1=3, e tamb¶m a
a e ca e
pot^ncia de x ¡ 3 de menor expoente:
e
1
y 0 = (x ¡ 3)¡1=3 ¢ [3(x ¡ 3)1 + 2(x + 2)]
3
1
= (x ¡ 3)¡1=3 ¢ (5x ¡ 5)
3
5
= (x ¡ 3)¡1=3 ¢ (x ¡ 1)
3
Para termos clareza quanto aos sinais de y 0 , reescrevemos y 0 usando radicais:
5(x ¡ 1)
y0 = p
3 3x¡3

8. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 64
ca e ³nua em todos os pontos de R, mas f 0 (x) n~o se de¯ne
Note que a fun»~o f ¶ cont¶ a
quando x = 3.
³zes do numerador e do denominador de y 0 s~o 1 e 3, sendo y 0 = 0 para
As ra¶ a
x = 1.
Temos ent~o o seguinte diagrama de sinais de y 0 , e correspondentes intervalos de
a
crescimento e decrescimento de f:
y' + 1 _ 3 + x
y pto de ∃ y'(3)
max
local pto de
min
y' = 0 local
Temos ent~o que f cresce em ] ¡ 1; 1], decresce em [1; 3] e cresce novamente
a
em [1; +1[. Aqui temos algo novo: f n~o tem derivada em x0 = 3, mas x0 = 3 ¶ um
a e
ponto de m¶³nimo local de f ! Como ¶ a geometria do gr¶¯co de f nas proximidades
e a
do ponto x0 = 3 ? A resposta a esta quest~o vir¶ com o estudo das concavidades do
a a
gr¶¯co.
a
Concavidades e in°ex~es da curva
o
Temos
· ¸0
00 5 ¡1=3
y = (x ¡ 3) ¢ (x ¡ 1)
3
¡5 5
= (x ¡ 3)¡4=3 (x ¡ 1) + (x ¡ 3)¡1=3
9 3
5 ¡4=3
= (x ¡ 3) [¡(x ¡ 1) + 3(x ¡ 3)1 ]
9
5
= (x ¡ 3)¡4=3 (2x ¡ 8)
9
10
= (x ¡ 3)¡4=3 (x ¡ 4)
9
Assim,
10(x ¡ 4)
f 00 (x) = p
9 3 (x ¡ 3)4
Temos o seguinte diagrama de sinais de y 00 e dire»oes de concavidades do gr¶¯co
p c~ a
de f (resista µ tenta»~o de simpli¯car o radical ( )
a ca 3 4) :
y'' _ 3 _ 4 +
y = f(x) x

9. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 65
O ponto (4; f (4)) = (4; 6) ¶ ponto de in°ex~o do gr¶¯co.
e a a
Deixamos ao leitor a veri¯ca»~o de que o gr¶¯co de f n~o tem retas ass¶
ca a a ³ntotas no
f (x)
in¯nito, pois lim x = +1.
x!§1
Com base nos elementos coletados acima, temos um esbo»o da curva y = f (x)
c
na ¯gura 7.4.
y
6
4
2
0 1 2 3 4 x
-2 -3
-2
Figura 7.4.
p
Neste esbo»o levamos em conta as aproxima»~es f(1) = 3 3 4 ¼ 3 ¢ (1; 6) = 4; 8,
p c co
f (0) = 2 3 9 ¼ 2 ¢ (2; 1) = 4; 2. Levamos em conta tamb¶m que ¡2 e 3 s~o ra¶ de f
e a ³zes
(isto ¶, solu»~es de f (x) = 0).
e co
Note que, antes e pouco depois de x0 = 3, o gr¶¯co tem concavidade voltada
a
para baixo. Como f decresce em [1; 3] e cresce em [3; +1[, temos, no gr¶¯co de f, a
a
forma»~o de um bico" agudo no ponto (3; 0). Isto explica a inexist^ncia de derivada
ca e
em x0 . N~o h¶ reta tangente ao gr¶¯co no ponto (3; 0).
a a a
Observa»~o 7.1 (O gr¶¯co de f em pontos com derivadas in¯nitas)
ca a
Quando f ¶ cont¶
e ³nua em um intervalo contendo um ponto x0 no seu interior, e f 0 ¶ e
³nua em todos os pontos desse intervalo, exceto em x0 e, al¶m disso, lim f 0 (x) =
cont¶ e
x!x0
+1 ou ¡1, temos uma reta vertical tangente ao gr¶¯co de f em P = (x0 ; f (x0 )).
a
Estes dois casos s~o ilustrados na ¯gura 7.5.
a
Quando lim+ f 0 (x) = +1 e lim¡ f 0 (x) = ¡1, o gr¶¯co forma um bico em P =
a
x!x0 x!x0
(x0 ; f(x0 )), tal como no ponto (3; 0) da ¯gura 7.4 ou no ponto P do gr¶¯co µ esquerda
a a
0 0
na ¯gura 7.6. Quando lim+ f (x) = ¡1 e lim¡ f (x) = +1, temos novamente um
x!x0 x!x0
bico em P , s¶ que agora apontando para cima, tal como no gr¶¯co µ direita na ¯gura
o a a
7.6.

10. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 66
P P
x0 x x0 x
Figura 7.5. A esquerda, limx!x0 f 0 (x) = ¡1. A direita, limx!x0 f 0 (x) = +1
µ µ
P
P
x0 x x0 x
Figura 7.6. A esquerda, limx!x+ f 0 (x) = +1, e limx!x¡ f 0 (x) = ¡1. A direita,
µ
0 0
µ
limx!x+ f 0 (x) = ¡1, e limx!x¡ f 0 (x) = +1
0 0
7.1 Problemas
³nuas, chamado teorema de Bolzano ou teo-
Um importante teorema sobre fun»~es cont¶
co
rema do anulamento, enuncia o seguinte:
Teorema de Bolzano Se f ¶ uma fun»~o cont¶
e ca ³nua no intervalo [a; b], com f (a) < 0
e f(b) > 0 (ou com f (a) > 0 e f (b) < 0), ent~o f tem uma raiz no intervalo ]a; b[,
a
isto ¶, existe x0 , a < x0 < b, tal que f (x0 ) = 0.
e
Na p¶gina 60, desta aula, temos uma vers~o equivalente desse teorema.
a a
Este teorema est¶ ilustrado nos gr¶¯cos das fun»~es (cont¶
a a co ³nuas) dos problemas 3
e 5, p¶gina 56, da aula 6. A fun»~o do problema 3 satisfaz f(0) > 0 e f (1) < 0, e
a ca
tamb¶m f(2) < 0 e f (3) > 0, o que lhe garante a exist^ncia de uma raiz entre 0 e 1, e
e e
de uma outra entre 2 e 3. J¶ a fun»~o do problema 5 possui uma raiz no intervalo ]2; 3[.
a ca
1. Usando o teorema do anulamento, enunciado acima, mostre que
(a) f(x) = x5 + x + 1 possui uma raiz no intervalo ]¡ 1; 0[.
(b) A equa»~o x3 ¡ 4x + 2 = 0 tem tr^s ra¶ reais distintas entre si.
ca e ³zes
2. Mostre que todo polin^mio p(x), de grau ¶
o ³mpar, com coe¯cientes reais, tem ao
menos uma raiz real.
Sugest~o. Considere os limites lim p(x) e lim p(x).
a
x!+1 x!¡1
Para cada uma das fun»~es dadas abaixo,
co

11. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 67
(a) Determine o dom¶ da fun»~o e, com base nisto, veri¯que se a curva y = f (x)
³nio ca
tem retas ass¶
³ntotas verticais.
(b) Calcule f 0 (x) e determine os intervalos em que f ¶ crescente e aqueles em que f
e
¶ decrescente;
e
³nimo locais de f , bem
(c) Determine os pontos de m¶ximo locais e os pontos de m¶
a
como os valores de f (x) nesses pontos;
(d) Calcule f 00 (x) e determine os intervalos em que a curva y = f (x) ¶ c^ncava para
e o
cima e aqueles em que ela ¶ c^ncava para baixo;
e o
(e) Determine os pontos de in°ex~o da curva y = f (x);
a
(f) Calcule as ra¶ de f (solu»~es da equa»~o f (x) = 0), quando isto n~o for dif¶
³zes co ca a ³cil;
(g) Veri¯que se a curva y = f(x) tem retas ass¶
³ntotas horizontais ou inclinadas.
(h) A partir dos dados coletados acima, fa»a um esbo»o bonito do gr¶¯co de f .
c c a
(i) Indique os pontos do gr¶¯co onde a reta tangente ¶ vertical e os pontos onde inexiste
a e
tal reta tangente (procure por pontos onde f ¶ cont¶
e ³nua, mas f 0 n~o ¶ de¯nida).
a e
x
3. f (x) =
x2 ¡ 2
x2
4. f (x) =
1+x
p3
5. f (x) = x2 ¡ 1
p
6. f (x) = 3 1 ¡ x3
p
7. f (x) = 3 6x2 ¡ x3
p
8. f (x) = 2x ¡ 2 3 x3 + 1
7.1.1 Respostas e sugest~es
o
Para os problemas de 3 a 8, daremos como resposta apenas as derivadas primeira e segunda,
e o esbo»o do gr¶¯co.
c a
x2 + 2 2x3 + 12x
3. f 0 (x) = ¡ , f 00 (x) = ¡ 2
(x2 ¡ 2)2 (x ¡ 2)3
2x + x2 00 2
4. f 0 (x) = 2
, f (x) =
(1 + x) (1 + x)3
2 ¡2
5. f 0 (x) = p , f 00 (x) = p
3 x
3 3
9 x4

12. Esbocando graficos: zeros no denominador e retas ass¶
» ¶ ³ntotas 68
¡x2 ¡2x
6. f 0 (x) = p , f 00 (x) = p
3
(1 ¡ x3 )2 3
(1 ¡ x3 )5
4x ¡ x2 ¡8x2
7. f 0 (x) = p , f 00 (x) = p
3
(6x2 ¡ x3 )2 3
(6x2 ¡ x3 )5
2x2 ¡4x
8. f 0 (x) = 2 ¡ p , f 00 (x) = p
3
(x3 + 1)2 3
(x3 + 1)5
Esbo»os dos gr¶¯cos:
c a
3. 4.
y y
x=-1
y= x-1
-1 0 x
− √−
− −
− x
2 0 √2
(-2,-4)
5. 6.
y y
(0,1)
(1,0)
x
-1 1 x
-1
(0,-1)
y = -x
7. 8.
y y
_ 0 x
3
(4,2√4 )
2
(-1,2) (0,-2)
0 2 (6,0) x
3
__
__ 3
__
__
( -√1/2 , -4√1/2 )
y = -x + 2 p
Dado num¶rico:
e 3
1=2 ¼ 0;8
p
3
Dado num¶rico:
e 4 ¼ 1;6