Este documento apresenta questões sobre conceitos fundamentais de matemática para um exame. A primeira questão pede para classificar um sistema de equações lineares e resolvê-lo para valores específicos. A segunda questão analisa propriedades de uma função, incluindo seu domínio, zeros, derivada e representação gráfica. A terceira questão pede para determinar primitivas de funções e calcular áreas. A quarta questão estuda a convergência de séries e calcula suas somas. A quinta questão trata de combinatórias envolvendo distribuição de técn

1. INSTITUTO SUPERIOR DE GESTÃO BANCÁRIA
CONCEITOS FUNDAMENTAIS DE MATEMÁTICA
Ano lectivo 2008/2009
Exame Época Normal
30 de Janeiro de 2009 Duração: 2 horas e 30 minutos
Resolução
1 - Considere o sistema de equações lineares:
⎧ x − y + 2z = 1
⎪
⎨ x − y + az = 2
⎪x + 4 y + 2z = b − 2
⎩
a) Classifique o sistema em função de a e b. (25)
Podemos utilizar o método de eliminação de Gauss para obter um sistema reduzido.
Assim, podemos começar por eliminar a incógnita x da segunda e da terceira equações:
− x + y − 2 z = −1
− E1 + E 2 : x − y + a z = 2
(a − 2) z = 1
− x + y − 2 z = −1
− E1 + E3 : x + 4 y + 2 z = b−2
5 y = b−3

2. O sistema vem agora equivalente a
⎧ −
⎪
⎨ ( a − 2) z = 1
⎪ = b−3
⎩ 5 y
Estamos agora em condições de classificar o sistema:
• Para α − 2 ≠ 0 ⇔ α ≠ 2 , ∀ b , o sistema é possível e determinado;
• Para α − 2 = 0 ⇔ α = 2 , ∀ b , o sistema é impossível;
• O sistema nunca é possível e indeterminado.
b) Resolva o sistema para a = 0 e b = 1. (15)
O determinante da matriz dos coeficientes vem
1 −1 2
1 − 1 0 = −2 + 0 + 8 − (−2 − 2 + 0) = 6 + 4 = 10 .
1 4 2
1
Por substituição ordenada no sistema reduzido, vem − 2 z = 1 ⇔ z = − . Substituindo
2
2
na segunda equação temos 5 y = −2 ⇔ y = − . Finalmente, substituindo na primeira
5
⎡ 8 ⎤
⎢ ⎥
⎡ x⎤ ⎢ 5 ⎥
equação vem x − y + 2 z = 1 ⇔ x = 1 − + 2 = . Assim, vem ⎢ y ⎥ = ⎢− ⎥ .
2 1 8 2
5 2 5 ⎢ ⎥ ⎢ 5⎥
⎢z⎥ ⎢ 1⎥
⎣ ⎦
⎢− 2 ⎥
⎣ ⎦
2 - Considere a função f, real de variável real, definida por:
⎧− x − 1 , x < −1
⎪
f ( x ) = ⎨− 2( x + 1) 2 ,−1 ≤ x < 1
⎪log( x − 1) ,x >1
⎩
a) Indique o domínio e os zeros da função. (15)
2

3. Para x < −1, f(x) é definida por uma função afim com domínio IR.. Para −1 ≤ x < 1 f(x) é
definida por uma parábola cujo domínio é IR e para x > 1 f(x) é definida por uma função
logarítmica que neste intervalo de valores de x se encontra definida. A função f(x) só
não está definida no ponto x=1, conclui-se assim que o seu domínio é IR {1}.
Zeros: − x − 1 = 0 ∧ x < −1 ⇔ x = −1 ∧ x < −1 impossível
− 2( x + 1) = 0 ∧ − 1 ≤ x < 1 ⇔ x = −1
2
log( x − 1) = 0 ∧ x > 1 ⇔ x = 2
Zeros: {−1, 2}.
b) Obtenha a função derivada f ' ( x) e mostre que não é diferenciável no ponto x=1.
(15)
A função derivada obtém-se por aplicação das regras de derivação aos vários ramos de
f(x). Uma vez que f(x) não está definida no ponto x=1, não admite derivada finita nesse
ponto e portanto não será diferenciável.
Derivadas laterais em x = −1
f (−1 + h) − f (−1) − (− 1 + h ) − 1 − 0 −h
f ' (−1− ) = lim− = lim− = lim− = −1
h →0 h h →0 h h →0 h
f (−1 + h) − f (−1) − 2(− 1 + h + 1) − 0 − 2h 2
2
+
f ' (−1 ) = lim+ = lim = lim+ = lim (−2h) = 0
h→0 h h →0 + h h→0 h h →0 +
como as derivadas laterais são diferentes não existe derivada em x = −1.
A função derivada vem:
⎧
⎪− 1 , x < −1
⎪
f ´( x ) = ⎨− 4 x − 4 , − 1 < x < 1
⎪ 1
⎪ , x >1
⎩ x −1
3

4. c) Indique os intervalos de monotonia e extremos relativos da função. (15)
O quadro de sinais vem
x −∞ −1 1 +∞
f'(x) − NE − ND +
f(x) 0 ND
NE-Não Existe; ND-Não Definida
Intervalos de monotonia:
A função é monótona decrescente para x∈ ]− ∞, 1[ .
A função é monótona crescente para x∈ ]1, + ∞[ .
Não há extremos relativos.
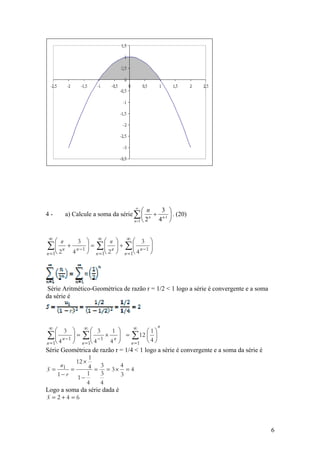
d) Represente graficamente a função. (15)
y
-1 1 2 x
-8
3-
4

5. a) Determine uma primitiva de cada uma das seguintes funções:
x 3
y= ey= . (15)
x 3x − 2
1 1
x x x1 1−
Primitivação da função y = : y= = 1 = x 2 = x2
x x x 2
1 3 3
+1
x2 2⋅ x2 2⋅ x x
1
x2
Assim, Y = P ( x ) =
2
= = = +k.
1 3 3 3
+1
2 2
3 3 −1
Primitivação da função y = : y= = 3 ⋅ (3 ⋅ x − 2) 2
3⋅ x − 2 3⋅ x − 2
1
−1 (3 ⋅ x − 2) 2 1
Y = P3 ⋅ (3 ⋅ x − 2) 2
= = 2 ⋅ (3 ⋅ x − 2) 2
=
Assim, 12
= 2 3⋅ x − 2 + k
b) Calcule a área do domínio plano definido pelas funções y = − x 2 + 1 e y = 0 . (15)
1
1 ⎛ x3 ⎞ ⎛ (1)3 ⎞ ⎛ (−1)3 ⎞ ⎛ 1 ⎞ ⎛1 ⎞ 4
∫−1 (− x + 1)dx = ⎜ − + x ⎟ = ⎜ −
⎜ 3 + 1⎟ − ⎜ − 3 + (−1) ⎟ = ⎜ − 3 + 1⎟ − ⎜ 3 + (−1) ⎟ = 3
2
⎜ 3 ⎟ ⎟ ⎜ ⎟
⎝ ⎠ −1 ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
Graficamente temos:
5

6. ∞
⎛ n 3 ⎞
4- a) Calcule a soma da série ∑ ⎜ n + n-1 ⎟ . (20)
n =1 ⎝ 2 4 ⎠
∞
⎛ n 3 ⎞ ∞⎛ n ⎞ ∞⎛ 3 ⎞
∑ ⎜ 2 n 4 n −1 ⎟ = ∑ ⎜ 2 n
⎜ + ⎟ ⎜ ⎟ + ∑⎜
⎟ ⎜ ⎟
⎟
⎠ n = 1⎝ 4 n − 1 ⎠
n = 1⎝ ⎠ n = 1⎝
Série Aritmético-Geométrica de razão r = 1/2 < 1 logo a série é convergente e a soma
da série é
∞ n
⎛ 3 ⎞ ∞⎛ 3 1 ⎞ ∞
⎛1⎞
∑ ⎜ 4 n −1 ⎟
⎜ ⎟ = ∑⎜ ⎜ −1 × ⎟ = ∑ 12 ⎜ ⎟
⎟
4n ⎠ n =1 ⎝ ⎠
n = 1⎝ ⎠ n = 1⎝ 4 4
Série Geométrica de razão r = 1/4 < 1 logo a série é convergente e a soma da série é
1
12 ×
u1 4 = 3 = 3× 4 = 4
S= =
1− r 1−
1 3 3
4 4
Logo a soma da série dada é
S = 2+4 =6
6

7. b) Estude a natureza das séries:
∞
n
i) ∑ n + 5 ; (10)
n =1
Condição Necessária de Convergência
Logo a série é divergente.
∞
5 2n
ii) ∑ n . (10)
n =1
Critério de Alembert
Logo a série é divergente.
5 – O Banco Central de um país tem uma equipa de 10 técnicos afectos ao
Departamento de Supervisão Bancária (DSB). Foi seleccionada uma amostra de 5
bancos para serem analisados pela referida equipa ao longo do mês de Fevereiro.
a) Quantas equipas de 3 técnicos pode o responsável do DSB constituir para efectuar a
análise pretendida? (20)
C 3 = 120 equipas diferentes.
10
b) De quantas formas pode o responsável do DSB distribuir essas equipas pelos bancos
que constituem a amostra admitindo que cada equipa só analisará um banco? (10)
120
A5 = 120 × 119 × 118 × 117 × 116 = 22869362880 formas diferentes.
7