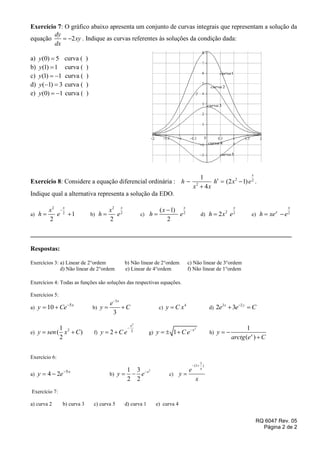
O documento apresenta uma lista de exercícios sobre equações diferenciais. Os exercícios incluem mostrar que determinadas funções são soluções de equações diferenciais, classificar equações diferenciais, verificar se funções são soluções, resolver equações diferenciais e problemas de valor inicial.

1. CÁLCULO 4 - EQUAÇÕES DIFERENCIAIS
LISTA DE EXERCÍCIOS 1
Exercício 1: Mostre que a função y  xe x é a solução da equação linear: y' '  2 y'  y  0 no intervalo
 ,  .
Exercício 2:
a) Mostre que as funções y1  c1cos 4x e y 2  c 2 sen 4x , onde c1 e c 2 são constantes arbitrárias, são
ambas as soluções da equação diferencial: y''  16y  0 .
b) Mostre que y  y1  y 2 também é solução da equação diferencial anterior.
Exercício 3: Classifique as equações diferenciais, considerando y(x), em lineares e não lineares e dê a
sua ordem:
a) 1  x  y''  4xy'  5y  cos x b) yy''  2 y  1  x 2
4
d3y  dy  d2y
c) x  2  y0 d)  9y  seny
 dx 
3
dx dx 2
e) x 3 y 4   x 2 y''  4xy'  3y  0 f) 1  y 2  dx  xdy  0
Exercício 4: Verifique se as funções apresentadas são soluções das respectivas equações diferenciais
dadas considerando y(x):
x
dy
a) 2y' y  0, y  e 2 b)  2y  e 3x , y  e 3x  10 e 2x
dx
c) y' 25  y 2 , y  5 tan 5x d)
dy
dx

y
x
,  
2
y  x  c1 , c1  0, x  0
2
d y dy
e) x 2
2  0, y  c1  c 2 x 1 f) x 2 y''  3xy' 4y  0, y  x 2  x 2 ln x, x  0
dx dx
Exercício 5: Resolva as equações:
dy dy
a)  5 y  50 b) dx  e3 x dy  0 c) x  4y
dx dx
dy
d) y '  e3 x  2 y e) y '  x 1  y 2 f)  2 x  xy
dx
g) ydy  x 1  y 2  dx
dy
h) (e x  e x )  y2
dx
Exercício 6: Resolva o problema de valor inicial:
 dy  dy
  5 y  20   2 xy  x  x 2 y '  y  xy
a)  dx b)  dx c) 
 y (0)  2  y (0)  1  y (1)  1
 
RQ 6047 Rev. 05
Página 1 de 2

2. Exercício 7: O gráfico abaixo apresenta um conjunto de curvas integrais que representam a solução da
dy
equação  2 xy . Indique as curvas referentes às soluções da condição dada:
dx
a) y(0)  5 curva ( )
b) y(1)  1 curva ( )
c) y(1)  1 curva ( ) curva 1
d) y(1)  3 curva ( ) curva 2
e) y(0)  1 curva ( )
curva 3
curva 4
curva 5
x
1
Exercício 8: Considere a equação diferencial ordinária : h  2 h  (2 x  1) e .
2 2
x  4x
Indique qual a alternativa representa a solução da EDO.
x
x2  2 x2 2x
( x  1) 2 x x x
a) h e 1 b) h e c) h e d) h  2 x2 e 2 e) h  xe x  e 2
2 2 2
_________________________________________________________________________________
Respostas:
Exercícios 3: a) Linear de 2°ordem b) Não linear de 2°ordem c) Não linear de 3°ordem
d) Não linear de 2°ordem e) Linear de 4°ordem f) Não linear de 1°ordem
Exercícios 4: Todas as funções são soluções das respectivas equações.
Exercícios 5:
e3 x
a) y  10  Ce5 x b) y C c) y  C x4 d) 2e3 x  3e2 y  C
3
x2
1 2  1
e) y  sen ( x  C ) y  2Ce y   1  C e x y
2
2
f) g) h)
2 arctg (e x )  C
Exercício 6:
1
 (1 )
x
1 3  x2 e
a) y  4  2e 5 x b) y   e c) y
2 2 x
Exercício 7:
a) curva 2 b) curva 3 c) curva 5 d) curva 1 e) curva 4
RQ 6047 Rev. 05
Página 2 de 2