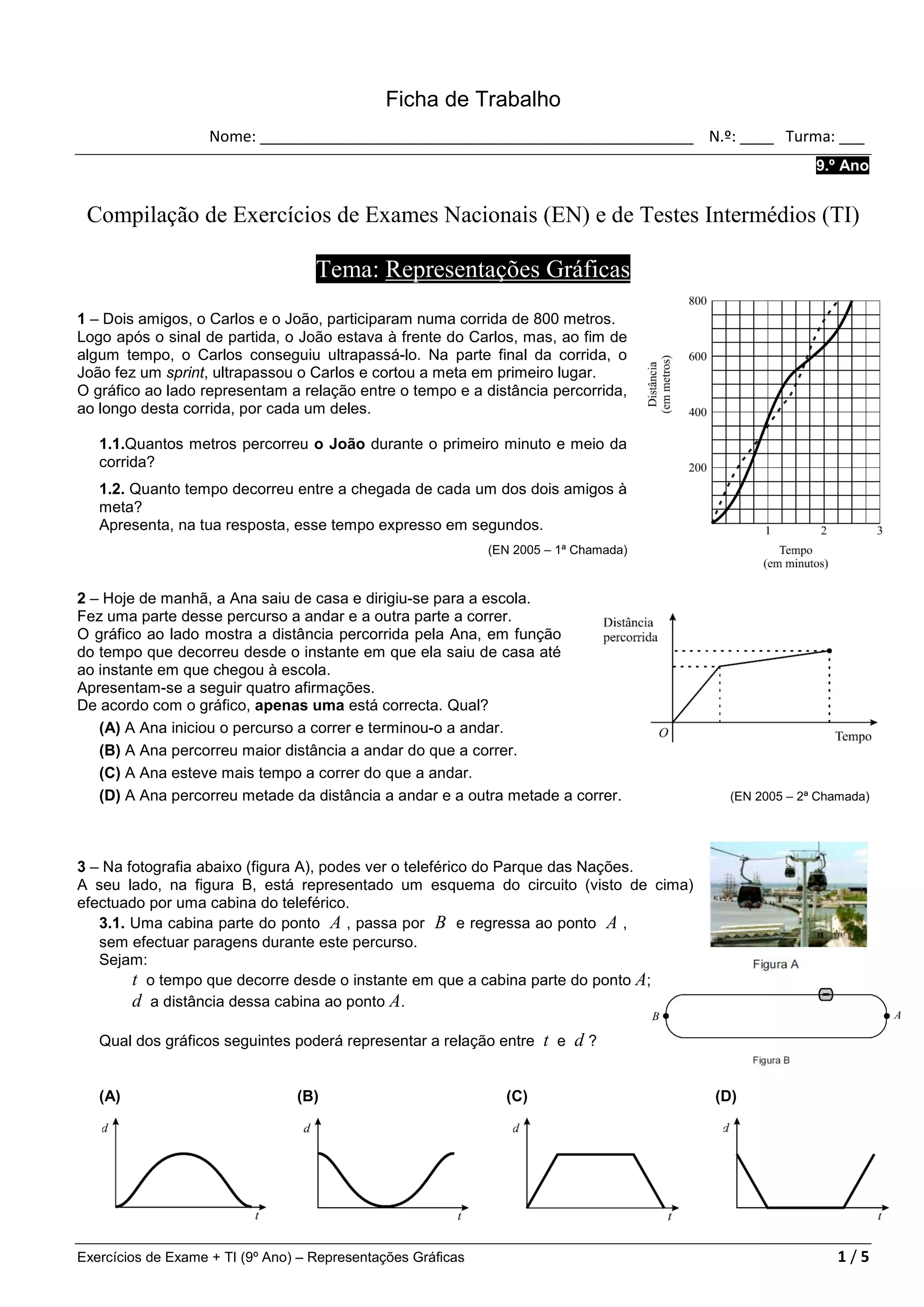
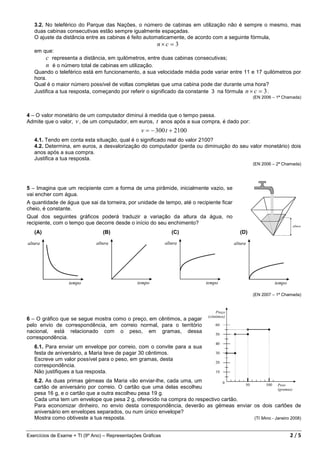
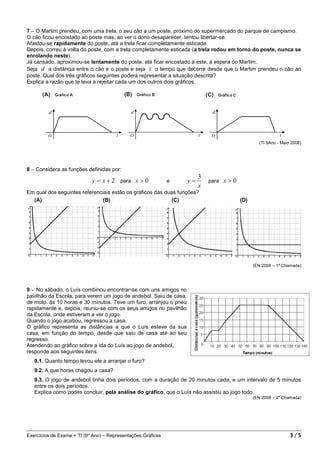
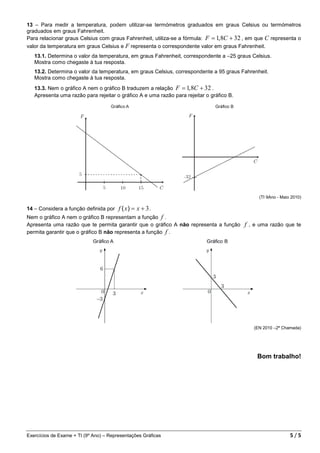
O documento apresenta uma compilação de exercícios sobre representações gráficas de vários exames nacionais e testes intermédios do 9o ano. Os exercícios abordam temas como corridas, deslocamentos, enchimento de recipientes, preços de envio de correspondência, e funções matemáticas.