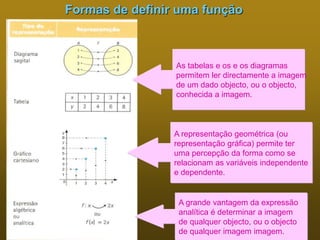
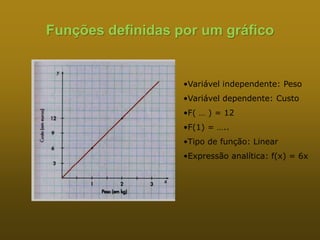
O documento discute conceitos fundamentais sobre funções, incluindo: 1) Funções podem ser definidas através de diagramas, tabelas, expressões analíticas ou gráficos. 2) Uma função é uma correspondência entre dois conjuntos onde cada elemento do primeiro conjunto está associado a exatamente um elemento do segundo conjunto. 3) Existem diferentes formas de representar funções e identificar seus domínios, conjuntos de chegada e contradomínios.

2. 1. Considere a figura seguinte e complete:
a) 5kg custam ___________ €.
b) Com 3,75€ posso comprar _______ kg
c) O dinheiro gasto ____________ ou é _____________ do
número de quilos adquiridos.

3. 2. Um avião desloca-se a uma velocidade média de 950km/h.
A partir da observação do gráfico, complete:
a)
Tempo
(Horas)
2 5 10
Distância
(km)
475 2850
b) O tempo de viagem __________________ ou é ________________
da distância percorrida.

4. Com os exemplos anteriores conseguimos estabelecer
correspondências entre:
• Dinheiro gasto e quantidade de laranjas comprada
• Tempo e distância
Assim, podemos dizer que:
• O preço a pagar depende ou é função da quantidade de
laranjas adquirida.
• O tempo de viagem depende ou é função da distância
percorrida.

5. 3. Para ter acesso a 30 horas de Internet é preciso pagar 60€.
 O preço a pagar depende ou é função do número de
horas de utilização.
 Ao número de horas chamamos variável independente
 Ao preço a pagar chamamos variável dependente

6. Conceito de função
Entre dois conjuntos não vazios podemos sempre
estabelecer uma correspondência.
 InglaterraEspanhaPortugalA ,,
 LondresMadridLisboaB ,,
 Todos os elementos de A estão
associados a um elemento de B
 Cada elemento de A está
associado apenas a um elemento de B
Uma correspondência entre dois conjuntos não
vazios A e B que a cada elemento do conjunto A
faz corresponder um e um só elemento do
conjunto B chama-se função.

8. 2ª aula

9. Retomemos a correspondência dada inicialmente.
 Esta correspondência é uma função a que passaremos a
chamar função f
 Os elementos do conjunto A chamam-se objectos e os
elementos do conjunto B chamam-se imagens.

10. O conjunto dos objectos chama-se conjunto de partida ou
domínio da função f e representa-se por
O conjunto B chama-se conjunto de chegada da função f.
O conjunto das imagens chama-se contradomínio da
função f e representa-se por
fD
 InglaterraEspanhaPortugalDf ,,
 Paris,,, LondresMadridLisboaB 
'
fD
 LondresMadridLisboaDf ,,'


11. Numa função podemos considerar três conjuntos:
 Domínio
 Conjunto de chegada
 Contradomínio
O contradomínio de uma função está sempre
contido no conjunto de chegada. Em algumas
funções estes conjuntos são iguais.

12. É COMO UMA MÁQUINA ONDE ENTRAM
FUNÇÃO
OBJECTOS
IMAGENSDEPOIS SÃO TRANSFORMADOS E SAEM

13. Consideremos agora a seguinte função:
Para indicar que -4 é a imagem de
-2, por meio da função f,
escrevemos:
Esta expressão lê-se:
f de menos dois é igual a menos
quatro.
4)2( f
Assim sendo, temos:
0)0( f 6)3( f

14. Exercício
Considere a correspondência de A para B definida na figura seguinte:
a) A correspondência é uma função? Justifique.
b) Indique o domínio da função.
c) Qual é o conjunto de chegada?
d) Qual é o contradomínio?
e) Complete:
12g(.....)-9g(.....)
.........g(2)........)1(

g

15. 3ª aula

16. Formas de definir uma função
As tabelas e os e os diagramas
permitem ler directamente a imagem
de um dado objecto, ou o objecto,
conhecida a imagem.
A representação geométrica (ou
representação gráfica) permite ter
uma percepção da forma como se
relacionam as variáveis independente
e dependente.
A grande vantagem da expressão
analítica é determinar a imagem
de qualquer objecto, ou o objecto
de qualquer imagem imagem.

17. Formas de definir uma função
As tabelas e os diagramas
de setas permitem ler
directamente a imagem de
um dado objecto, ou o
objecto conhecida a
imagem.
A grande vantagem da expressão
analítica é determinar a imagem
de qualquer objecto ou o objecto
de qualquer imagem.
A representação geométrica ou
representação gráfica permite ter
uma percepção da forma como se
relacionam as variáveis independente
e dependente.

19. Qualquer uma destas representações tem as suas
vantagens.
 As tabelas e os diagramas de setas permitem ler directamente a imagem
de um dado objecto, ou o objecto conhecida a imagem.
 A grande vantagem da expressão analítica é determinar a imagem de
qualquer objecto ou o objecto de qualquer imagem.
 A representação geométrica ou representação gráfica permite ter uma
percepção da forma como se relacionam as variáveis independente e
dependente.
Também podemos definir uma função através de uma expressão
verbal. Por exemplo: “Considere a função que a cada número faz
corresponder o dobro desse número.”

20. 4ª aula

21. Proporcionalidade directa
A Maria e o Tomás vão pintar uma casa.
O folheto da fábrica que produz a tinta traz uma tabela onde as grandezas
capacidade e área estão representadas por C e A, respectivamente.
12
Nesta tabela, a Maria e o Tomás observaram o seguinte:
• 1 litro de tinta dá para pintar 12 m2.
• Ambas as grandezas aumentam, isto é, quando C aumenta para o dobro, A
também aumenta para o dobro; quando C aumenta para o triplo, A também
aumenta para o triplo; etc
• Os valores da grandeza A obtêm-se multiplicando os valores de C por 12;
• O quociente entre valores correspondentes das duas grandezas dá sempre 12;
Então, as grandezas C e A são directamente proporcionais.
C (Litros) 1 2 3 6 9
A (m2) 12 24 36 72 108

22. C (Litros) 1 2 3 6 9
A (m2) 12 24 36 72 108
12
12
9
108
6
72
3
36
24
2
1
12

12K
Constante de proporcionalidade
Para que haja proporcionalidade directa é preciso que todos os
quocientes sejam iguais (neste caso são iguais a 12).
Duas grandezas A e B são directamente proporcionais desde que o
valor de uma se obtenha multiplicando os valores da outra por um
mesmo número, diferente de zero. A esse número chama-se constante
de proporcionalidade directa e representa-se pela letra k.
A variável y é directamente proporcional a x se existe um número
k, diferente de zero, de modo que
Ao número c chama-se constante de proporcionalidade.
kxy 

23. A variável y é directamente proporcional a x se existe um número
k, diferente de zero, de modo que
Ao número c chama-se constante de proporcionalidade.
O valor da constante de proporcionalidade é o quociente entre dois
quaisquer valores correspondentes não nulos.
Para averiguar se existe proporcionalidade directa entre duas variáveis
verificamos se a razão entre cada par de valores correspondentes é
constante.

24. Exercício
Verifique se y é directamente proporcional a x.
x 12 10 50
y 7,2 15 30
5,1
10
15
mas6,0
50
30
12
2,7

Como existe um quociente que não é
igual aos outros, y não é directamente
proporcional a x.
Resolução:

25. Diariamente resolvemos problemas envolvendo relações de proporcionalidade
directa.
As formas mais comuns de resolução de problemas consistem em usar a regra de
três simples ou a redução à unidade.
Método de redução à unidade
Quanto custa 1kg de arroz?
6:5=1,20
7x1,20=8,40
A Rita pagou 8,40€ por 7kg de arroz
Método da regra de três simples
Peso (kg) Custo (€)
5 6
7 x
5x = 7x6, ou seja,
A Rita pagou 8,40€ por 7kg de arroz
4,8
5
42
5
67


 xxx
Exemplo:
A Joana comprou 5kg de arroz por 6€ e a Rita comprou 7kg do
mesmo arroz. Quanto pagou a Rita pelo arroz?

26. Proporcionalidade directa como função

29. Funções definidas por um diagrama
Ex. Não são funções
Ex. Funções
1
2
3
4
-1
-2
-3
1
2
-1
2
1
2
3
-1
-7
-2
-4
-3
A B
Df = {1;2,3}
D’f = {-1;-2,-3}
Objectos: 1;2,3
Imagens: -1;-2;-3
A – Conjunto de Partida
B – Conjunto de chegada
f ( 2 ) = -2
f ( x ) = -x
f

30. Funções definidas por uma Tabela
Df = {1;2,3;4}
D’f = {4;8;12;16}
Objectos: 1;2,3;4
Imagens: 4;8;12;16
Variável independente: Lado do quadrado
Variável dependente: Perímetro do quadrado
f ( 2 ) = 8
f ( x ) = 4x
Seja a função f definida pela tabela seguinte
Lado de um quadrado (L) 1 2 3 4
Perímetro do quadrado (P) 4 8 12 16

31. Funções definidas por uma expressão
analítica
Seja a função f definida pela seguinte expressão analítica
f(x ) = 2x -1
•Calcular a imagem sendo dado o objecto
f(3) = 2 x 3 -1
f(3) = 5
•Calcular o objecto sendo dada a imagem
f(x) = 15
2x – 1 = 15
 2x = 15 + 1
 2x = 16
 x = 8
(3;5) e (8;15)
pertencem á recta que é
gráfico da função f.

32. Funções definidas por um gráfico
•Variável independente: Peso
•Variável dependente: Custo
•F( … ) = 12
•F(1) = …..
•Tipo de função: Linear
•Expressão analítica: f(x) = 6x

33. Funções
Definição : Uma função é uma correspondência entre A e B
Formas de definir uma função:
•Por um diagrama
•Por uma tabela
•Por uma expressão analítica
•Por um gráfico

34. Função é uma correspondência entre 2 variáveis,
que a cada objecto (variável independente) faz
corresponder uma e uma só imagem (variável
dependente).
PORTO
BENFICA
SPORTING
VERMELHO
VERDE
AZUL
AMARELO
•
•
•
•
•
•
•
A B

35. Conceito de função
Entre dois conjuntos não vazios podemos sempre
estabelecer uma correspondência.
 InglaterraEspanhaPortugalA ,,
 LondresMadridLisboaB ,,
 Todos os elementos de A estão
associados a um elemento de B
 Cada elemento de A está
associado apenas a um elemento de B

36. Uma correspondência entre dois conjuntos não
vazios A e B que a cada elemento do conjunto A
faz corresponder um e um só elemento do
conjunto B chama-se função.