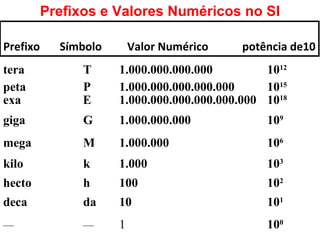
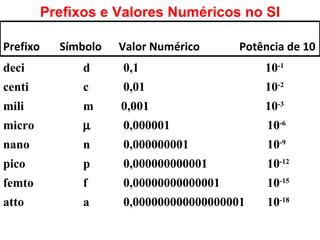
O documento explica sobre a notação científica, que é uma forma de representar números muito grandes ou pequenos usando potências de 10. Ele descreve como transformar números para esta notação através de deslocar a vírgula e como realizar operações matemáticas com números nesta notação, preservando os expoentes. Também apresenta o Sistema Internacional de Unidades e seus prefixos para expressar quantidades maiores ou menores que as unidades padrão.

1. ORDEM DE GRANDEZA

2. Muitas vezes também trabalhamos com números muito pequenos. Exemplo: Massa de um átomo (C):0,000 000 000 000 000 000 000 000 1992 . 10 -27 Kg A Notação científica é uma forma de representar números muito grandes ou muito pequenos, baseada no uso de potências de base 10. Existem algumas vantagens em utilizarmos a notação científica: os números muito grandes ou muito pequenos podem ser escritos de forma reduzida; torna os cálculos mais rápidos e fáceis; é utilizada por computadores e máquinas de calcular.

3. Um número estará em notação científica quando estiver escrito no seguinte formato: a x 10 m a é um valor qualquer compreendido entre 1 e 10, multiplicado por uma potência de base 10 e m é o expoente que pode ser positivo ou negativo Ex: 3000 = 3 .10 3 0,003 = 3 .10 -3 Nota: Usamos expoentes positivos quando estamos representando números grandes e expoentes negativos quando estamos representando números pequenos.

4. REGRA PRÁTICA Números maiores que 1 Deslocamos a vírgula para a esquerda até colocarmos o número com um valor entre 1 e 10. O número de casas deslocadas para a esquerda corresponderá ao expoente positivo da potência de 10. Exemplos: 2000 = 2 .10 3 762500 = 7,625 .10 5

5. Números menores que 1 Deslocamos a vírgula para a direita até colocarmos o número com um valor entre 1 e 10. O número de casas deslocadas para a direita corresponderá ao expoente negativo da potência de 10. Exemplos: 0,0008 = 8.10 -4 0,000000345 = 3,45 .10 -7

6. Operações com notação científica Adição Para somar números escritos em notação científica, é necessário que o expoente seja o mesmo. Se não o for temos que transformar uma das potências para que o seu expoente seja igual ao da outra. Exemplo: (5 . 10 4 ) + (7,1 . 10 2 ) = = (5 . 10 4 ) + (0,071 . 10 4 ) = = (5 + 0,071) . 10 4 = 5,071 . 10 4

7. Subtração Na subtração também é necessário que o expoente seja o mesmo. O procedimento é igual ao da soma. Exemplo: (7,7 . 10 6 ) - (2,5 . 10 3 ) = = (7,7 . 10 6 ) - (0,0025 . 10 6 ) = = (7,7 - 0,0025) . 10 6 = 7,6975 . 10 6

8. Multiplicação Multiplicamos os números sem expoente, mantemos a potência de base 10 e somamos os expoentes de cada uma. Exemplo: (4,3 . 10 3 ) . (7 . 10 2 )= = (4,3 . 7) . 10 (3+2) = 30,1 . 10 5 Para que a resposta seja dada na forma de potência de 10, teremos:

9. Divisão Dividimos os números sem expoente, mantemos a potência de base 10 e subtraímos os expoentes. Exemplo: = =

10. O SISTEMA MÉTRICO

11. O sistema métrico ou Sistema Internacional (SI) é um sistema decimal de unidades. É construído em torno de unidades padrão. Usa prefixos representando potências de 10 para expressar quantidades que são maiores ou menores do que as unidades padrão.

12. SI Unidades Básicas de Medida Quantidade Unidade Símbolo Comprimento metro m Massa kilograma kg Temperatura Kelvin K Tempo segundo s Quantidade de matéria mol mol Corrente Elétrica ampere A Intensidade da Luz candela cd

13. SI Unidades Derivadas de Medida Quantidade Unidade Símbolo Velocidade (d/t) metros/segundo m/s Aceleração (v/t) metros/segundo 2 m/s 2 Força (m.a) Newton N Pressão (F/A ) Pascal Pa Energia Joule J Potência Watt W

14. Prefixos e Valores Numéricos no SI Prefixo Símbolo Valor Numérico potência de10 exa E 1.000.000.000.000.000.000 10 18 peta P 1.000.000.000.000.000 10 15 tera T 1.000.000.000.000 10 12 giga G 1.000.000.000 10 9 mega M 1.000.000 10 6 kilo k 1.000 10 3 hecto h 100 10 2 deca da 10 10 1 — — 1 10 0

15. deci d 0,1 10 -1 centi c 0,01 10 -2 mili m 0,001 10 -3 micro  0,000001 10 -6 nano n 0,000000001 10 -9 pico p 0,000000000001 10 -12 femto f 0,00000000000001 10 -15 atto a 0,000000000000000001 10 -18 Prefixo Símbolo Valor Numérico Potência de 10 Prefixos e Valores Numéricos no SI

16. ORDEM DE GRANDEZA

17. Ao fazermos um cálculo aproximado, é comum darmos como resposta a potência de dez mais próxima do resultado calculado e a resposta dada dessa maneira é chamada de ordem de grandeza . Para determinar a ordem de grandeza de um número, devemos seguir os seguintes passos : 1º passo: Passe o número para a notação científica : x = N.10 n , com 1  N  10. 2º passo: Olhando para o valor de N: se N  3,16, faça n + 1. se N  3,16, n fica com o mesmo valor. O motivo de se arredondar dessa maneira é que o ponto médio entre o intervalo de duas potências consecutivas, tipo 10 0 e 10 1 é 10 0,5 , pois

18. Velocidade da luz no vácuo: 3 . 10 5 Km/s Diâmetro de um átomo (H): 1 . 10 -10 m Quantidade de moléculas em 1 mol de uma substância qualquer: 6,022 . 10 23 Tempo de reação para pisar no freio: Quantidade de água nos oceanos da Terra: 1,35 . 10 21 L Duração de uma piscada: 2 . 10 -1 s EXEMPLOS DE ORDEM DE GRANDEZA