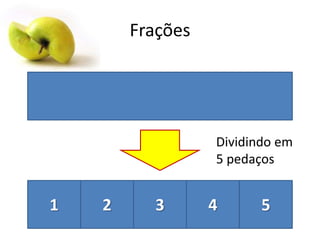
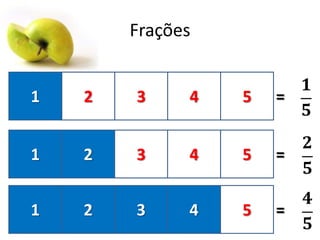
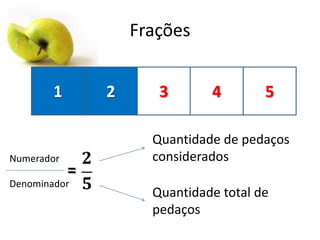
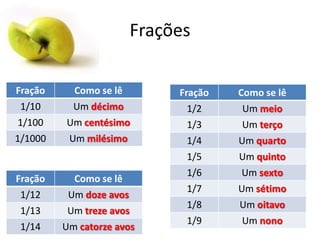
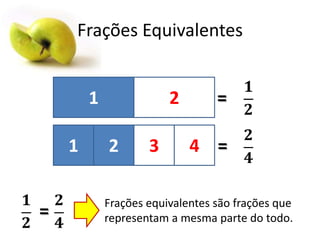
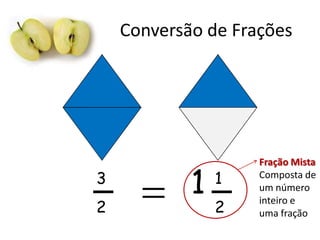
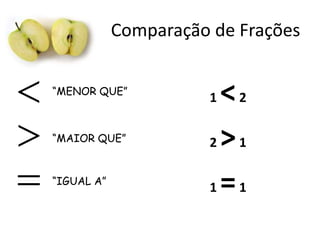
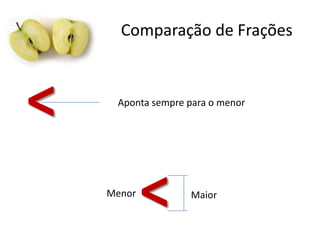
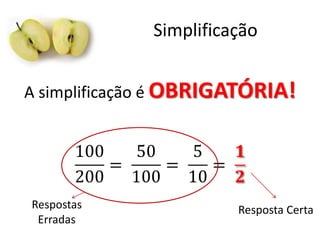
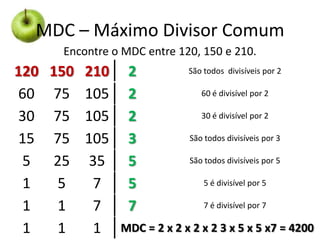
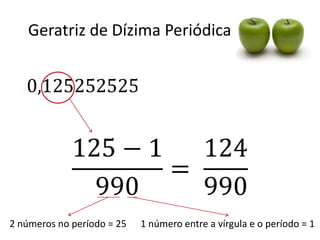
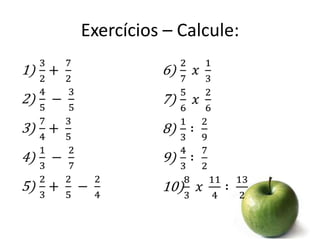Este documento fornece uma introdução às frações, incluindo como ler e escrever frações, classificá-las, encontrar frações equivalentes, comparar frações, e realizar operações básicas com frações como adição, subtração, multiplicação e divisão. O documento também explica como converter entre frações e números decimais.

1. Unidade 2 - Frações
Prof. Milton Henrique
mcouto@catolica-es.edu.br

2. Frações
Dividindo em
5 pedaços
1
2
3
4
5

3. Frações
1
2
3
4
5
=
1
2
3
4
5
=
1
2
3
4
5
=

4. Frações
1
Numerador
2
=
Denominador
3
4
5
Quantidade de pedaços
considerados
Quantidade total de
pedaços

5. Fração é uma Divisão

6. Frações
Fração
1/10
Como se lê
Um décimo
1/100
1/1000
Um centésimo
Um milésimo
Fração
Como se lê
1/12
1/13
1/14
Um doze avos
Um treze avos
Um catorze avos
Fração
Como se lê
1/2
1/3
1/4
Um meio
Um terço
Um quarto
1/5
1/6
1/7
1/8
1/9
Um quinto
Um sexto
Um sétimo
Um oitavo
Um nono

7. Classificação das Frações
• Própria
– Numerador menor que o denominador
• 3/5, 7/9, 2/7, etc.
• Imprópria
– Numerador maior ou igual ao denominador
• 5/4, 3/3, 8/3, etc.
• Aparente
– Numerador é múltiplo do denominador
• 6/3, 24/12, 9/3, etc.

8. Frações Equivalentes
1
1
=
2
2
3
=
4 =
Frações equivalentes são frações que
representam a mesma parte do todo.

9. Frações Equivalentes
Multiplicar o numerador e o denominador por
um mesmo valor não altera as frações

10. Conversão de Frações
3
2
1
1
2
Fração Mista
Composta de
um número
inteiro e
uma fração

11. Comparação de Frações
“MENOR QUE”
“MAIOR QUE”
“IGUAL A”
<2
2>1
1=1
1

12. Comparação de Frações
<
Aponta sempre para o menor
Menor
<
Maior

13. Comparação de Frações
5
1
2
2
5
4

14. Exercícios – Compare
as Frações

15. Simplificação
A simplificação é OBRIGATÓRIA!
Respostas
Erradas
Resposta Certa

16. MMC – Mínimo Múltiplo Comum
Encontre o MMC entre 120, 150 e 210.
120 150 210
60 75 105
20 25 35
4
5
7
2
3
5
São todos divisíveis por 2
São todos divisíveis por 3
São todos divisíveis por 5
Não são mais divisíveis pelo mesmo número
MMC = 2 x 3 x 5 = 30

17. MDC – Máximo Divisor Comum
Encontre o MDC entre 120, 150 e 210.
120
60
30
15
5
1
1
1
150
75
75
75
25
5
1
1
210
105
105
105
35
7
7
1
2
2
2
3
5
5
7
São todos divisíveis por 2
60 é divisível por 2
30 é divisível por 2
São todos divisíveis por 3
São todos divisíveis por 5
5 é divisível por 5
7 é divisível por 7
MDC = 2 x 2 x 2 x 2 3 x 5 x 5 x7 = 4200

18. MMC e MDC
MMC = Mínimo
→ Sempre Menor que os números
MMC entre 120, 150 e 210 = 30
MDC = Máximo
→ Sempre Maior que os números
MDC entre 120, 150 e 210 = 4200

19. Exercícios
Calcule o MMC e o MDC dos
números abaixo:
1)
2)
3)
4)
5)
6)
35, 81, 144
4,9,12
2,4,8
1,25,100
48,64,96
3,21,42

20. Operações com Frações
(Adição e Subtração)
Denominadores IGUAIS
 Neste caso somamos e subtraímos o
numerador e conservamos o denominador
Exemplo 1:
Exemplo 2:

21. Operações com Frações
(Adição e Subtração)
Denominador DIFERENTES
 Neste caso reduzimos as frações ao mesmo
denominador e prosseguimos como o caso
anterior
Exemplo:

22. Operações com Frações
(Multiplicação)
 Neste caso basta multiplicar os numeradores
entre si e os denominadores também entre si
Exemplo:

23. Operações com Frações
(Divisão)
 Neste caso basta inverter uma fração e depois
proceder como uma multiplicação normal
Exemplo:
Fração Invertida

24. Exercícios – Calcule:

25. Transformação de Frações
em Números Decimais
• De modo usual, divide-se o numerador pelo
denominador
Exemplo 1:
Exemplo 2:

26. Transformação de Números
Decimais em Frações
Transforme em número fracionário o número
decimal 23,453434...
Partes decimais
idênticas
-

27. Dízima Periódica
Aos numerais decimais em que há repetição
periódica e infinita de um ou mais algarismos,
dá-se o nome de numerais decimais periódicos
ou dízimas periódicas.
Período da dízima
Período da dízima
SIMPLES
COMPOSTA
Período logo após a vírgula
Existe uma parte não periódica
entre a vírgula e o período

28. Geratriz de Dízima Periódica
É a fração que deu origem a uma dízima periódica.
• Dízima Simples
– A geratriz de uma dízima simples é uma fração que tem para
numerador o período e para denominador tantos noves
quantos forem os algarismos do período.

29. Geratriz de Dízima Periódica
• Dízima Composta
– A geratriz de uma dízima composta é uma fração da forma
n/d , onde:
• n é a parte não periódica seguida do período, menos a parte
não periódica.
• d tantos noves quantos forem os algarismos do período
seguidos de tantos zeros quantos forem os algarismos da
parte não periódica.

30. Geratriz de Dízima Periódica
2 números no período = 25
1 número entre a vírgula e o período = 1

31. Exercícios – Escreva a Forma
Fracionária
1)
2)
3)
4)
5)
17,3443434343434...
4,59222...
4,12
0,0432
0,75

32. Quem sou eu?
Prof. Milton Henrique do Couto Neto
mcouto@catolica-es.edu.br
Engenheiro Mecânico, UFF
MBA em Gestão Empresarial, UVV
MBA em Marketing Empresarial, UVV
Mestre em Administração, UFES
Pós-MBA em Inteligência Empresarial, FGV
http://lattes.cnpq.br/8394911895758599

33. Professor Universitário
2004
2011
2006
2007
2009
2011

34. Disciplinas
Lecionadas
Marketing
Empreendedorismo
Administração de Materiais
Matemática
Matemática Financeira
Gestão Financeira
Fundamentos da Administração
Gestão de Processos e Empresas

35. miltonhenrique
miltonhcouto
miltonhcouto

36. Este e outros arquivos estão
disponíveis para download no
www.slideshare.net/miltonh