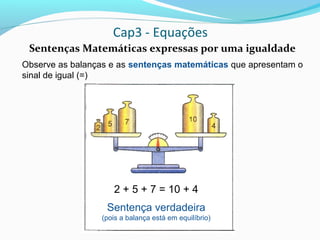
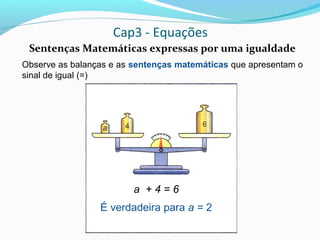
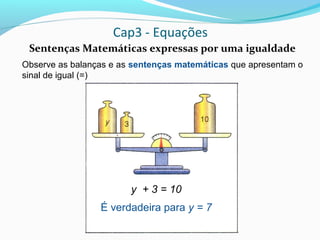
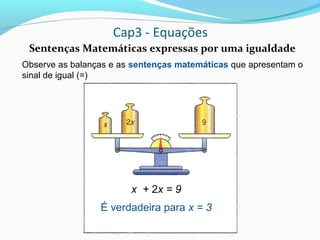
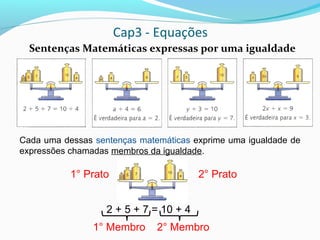
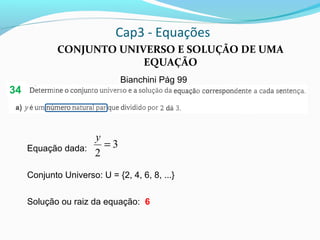
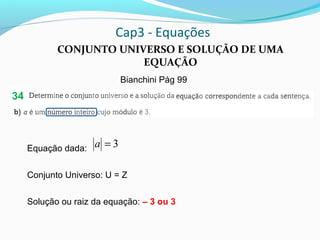
1) O documento apresenta conceitos fundamentais de álgebra, como expressões algébricas, termos algébricos, equações e raiz de equações; 2) Uma equação é uma sentença matemática expressa por uma igualdade que contém letras representando números desconhecidos; 3) Para verificar se um número é a raiz de uma equação, substitui-se a incógnita pelaquele número e verifica-se se a sentença resultante é verdadeira.

1. CENTRO EDUCAÇÃO SESC JOSÉ ROBERTO
TADROS
MATEMÁTICA – 7º ANO
Professor: Jonei Mangabeira
EQUAÇÕES

2. Cap3 - Equações
Você é daqueles que acha que na Matemática tudo
é número e que as letras fazem parte do curso de
português?
As letras na Matemática servem para representar
números desconhecidos ou mesmo para
generalizar propriedades.
2n – representa os números pares;
an
- representa uma potência;
am
: an
= am - n
- representa o quociente de potência de mesma base
x.y=y.x - ?

3. Cap3 - Equações
UM POUCO DE HISTÓRIA
Esses estudos de letras na Matemática fazem parte
do que chamamos de Álgebra.
Expressões que apresentam letras são chamadas de
expressões algébricas.
O matemático árabe al-
Khowarismi escreveu o
livro Al-jabr-Wa´l
muqabalar, cujo título
possivelmente deu
origem ao termo
ÁLGEBRA

4. Cap3 - Equações
UM POUCO DE HISTÓRIA
Os textos mais antigos de Matemática, como os
egípcios, os babilônicos, os indianos e os arábes
eram compostos de uma lista de problemas cujas
soluções eram fornecidas posteriormente.
Vejamos um desses problemas:
“A quantidade e sua [quarta parte] adicionados dão
15. Qual é a quantidade?”
Papiro Rhind

5. Cap3 - Equações
EXPRESSÕES ALGÉBRICAS
Podemos traduzir informações da linguagem
comum para a linguagem matemática:
•Dois somado a cinco ---> 2 + 5
•Três vezes quatro mais um ----> 3.4 + 1
•o quadrado de dois sétimos adicionado a dois
quintos ---->
5
2
7
2
2
+






6. Cap3 - Equações
EXPRESSÕES ALGÉBRICAS
Em algumas situações usamos letras para representar
números. Usando x para representar um número
racional, temos:
•O dobro de um número -----> 2.x ou 2x
•Triplo de um números menos 2 ----> 3x – 2
•Três quartos de um número ----> x
4
3
Não é
necessário
escrever o sinal
de multiplicação
entre um
número e uma
letra

7. Cap3 - Equações
EXPRESSÕES ALGÉBRICAS
Em todos os exemplos de expressões algébricas
(expressões com letras) apresentados, o número x é
chamado de VARIÁVEL (pois x pode assumir qualquer
número racional)
Vejas as seguintes expressões algébricas e suas variáveis.
Em uma expressão algébrica, a variável não precisa ser
obrigatoriamente a letra x. Ela pode ser qualquer outra letra.

8. Cap3 - Equações
EXPRESSÕES ALGÉBRICAS
Em todos os exemplos de expressões algébricas
(expressões com letras) apresentados, o número x é
chamado de VARIÁVEL (pois x pode assumir qualquer
número racional)
Vejas as seguintes expressões algébricas e suas variáveis.
x2
O dobro de um número
103 −x
O triplo de um número menos dez
32
2
tt
−





O quadrado da metade de um número menos um terço
desse númeroA soma de um número com o dobro de outro número
ba 2+
O produto de dois números diferentes
xy

9. Cap3 - Equações
VALOR NUMÉRICO DE UMA EXPRESSÃO
ALGÉBRICA
Podemos substituir as variáveis de uma expressão algébrica por
números e encontrar um valor numérico.
Considere o retângulo em que x representa a medida da base e y a
medida da altura.
O perímetro desse retângulo é dado pela expressão:
2x + 2y
Vamos calcular o perímetro de um retângulo que tenha 50 cm como
medida da base e 20 cm como medida da altura.
cmx 50=
cmy 20=
( ) ( ) 1404010020250222 =+=⋅+⋅=+ yx

10. Cap3 - Equações
VALOR NUMÉRICO DE UMA EXPRESSÃO
ALGÉBRICA
No exemplo dado, o perímetro do retângulo de base 50 cm e altura
20cm é 140cm. Neste caso dizemos que:
140 é o valor numérico da expressão 2x + 2y para x = 50 e y = 20.
O Valor numérico de uma expressão algébrica é o número que se
obtém ao substituir as letras por números e efetuamos as operações
indicadas.

11. Cap3 - Equações
VALOR NUMÉRICO DE UMA EXPRESSÃO
ALGÉBRICA
Veja mais um exemplo:
Quando uma letra representar um número negativo, uma fração
ou um número decimal, devemos colocar os números dentre de
parênteses.

12. Cap3 - Equações
TERMO ALGÉBRICO
Observe as seguintes expressões algébricas:
4x2
2xy
Cada expressão é chamada de termo algébrico (produto de números
e letras)
Em um termo algébrico distinguimos o Coeficiente ( Parte numérica) e
a Parte Literal (parte com letra).
No exemplos dados, temos:
4x2
----> Coeficiente: 4 Parte Literal: x2
2xy ----> Coeficiente: 2 Parte Literal: xy

13. Cap3 - Equações
TERMO ALGÉBRICO
Observações: Exemplo
•Não é necessário escrever o sina de multiplicação
entre números e letras
•Não é necessário escrever o expoente 1
•Quanto o termo tem coeficiente 1, indica-se apenas a
parte literal.
•Quanto o termo tem coeficiente –1, indica-se apenas
a parte literal com o sinal –
331
xyyx =⋅
aa 22 =⋅
abab =1
yzyz 22
1 −=−

14. Cap3 - Equações
TERMO ALGÉBRICO
Termo algébrico Coeficiente Parte literal
Não tem
Na tabela a seguir, temos expressões algébricas com seus coeficiente
e sua parte literal:
x5 5 x
m− 1− m
2
4
3
xy−
4
3
−
2
xy
6
ax
−
6
1
− ax
8 8

15. Cap3 - Equações
TERMOS SEMELHANTES
Termos que têm a mesma parte literal, ou que não tem parte literal,
são chamados de TERMOS SEMELHANTES.
e São termos semelhantes
Podemos adicionar algebricamente termos semelhantes, aplicando a
propriedade distributiva da multiplicação em relação à adição.
• 2x + 6x = (2 + 6)x = 8x
• 7x3
y2
– 5x3
y2
= (7 – 5)x3
y2
= 2x3
y2
• 2ax + b+3ax – 2b = 2ax +3ax + b– 2b =
= (2 + 3)ax + (1 – 2)b =
= 5ax – b
yx2
12 yx2
5
A este processos chamamos
de simplificação de
expressões
algébricas

16. Cap3 - Equações
TERMOS SEMELHANTES
Bianchini Pág 95

×


×
×
×

13
14

17. Cap3 - Equações
SIMPLICAÇÃO DE EXPRESSÕES ALGÉBRICAS
1) Simplifique as seguintes expressões algébricas:
a)5x + 7x =
b)a + a + a + a =
c)– 6a – 2a + 5a =
d)4x2
+ 5x + y
12x
3a
– 3a
Já está simplificada (Não há termos semelhantes para reduzir)

18. Cap3 - Equações
SIMPLICAÇÃO DE EXPRESSÕES ALGÉBRICAS
e)
23
94 xx
+
+
Separamos em duas frações
=+
+
23
94 xx
=++
23
9
3
4 xx
=+





+ 3
2
1
3
4
x =+ 3
6
11
x
Termos reduzidos
Expressão simplificada!!!
=+
+
23
94 xx
3
6
11
+x

19. Cap3 - Equações
SIMPLICAÇÃO DE EXPRESSÕES ALGÉBRICAS
f) ( ) xx ++⋅ 62
Propriedade Distribuitiva da Multiplicação
=++ xx 122( ) =++⋅ xx 62 123 +x
( ) =++⋅ xx 62 123 +x

20. Cap3 - Equações
SENTENÇAS MATEMÁTICAS
Sentença é um conjunto de palavras com sentido completo.
 Samuel é aluno do 7° ano B (Sentença verdadeira)
 Jonei é professor de Língua Portuguesa (Sentença FALSA)
 O Prof. Jonei tem mais idade que seus alunos (Sentença verdadeira)
Quando uma sentença envolve números, ela é chamada de
SENTENÇA MATEMÁTICA.
Cinco mais três é igual a sete
 Sete é diferente de nove.
Doze é dobro de seis.

21. Cap3 - Equações
Sentenças Matemáticas expressas por uma igualdade
Observe as balanças e as sentenças matemáticas que apresentam o
sinal de igual (=)
2 + 5 + 7 = 10 + 4
Sentença verdadeira
(pois a balança está em equilíbrio)

22. Cap3 - Equações
Sentenças Matemáticas expressas por uma igualdade
Observe as balanças e as sentenças matemáticas que apresentam o
sinal de igual (=)
a + 4 = 6
É verdadeira para a = 2

23. Cap3 - Equações
Sentenças Matemáticas expressas por uma igualdade
Observe as balanças e as sentenças matemáticas que apresentam o
sinal de igual (=)
y + 3 = 10
É verdadeira para y = 7

24. Cap3 - Equações
Sentenças Matemáticas expressas por uma igualdade
Observe as balanças e as sentenças matemáticas que apresentam o
sinal de igual (=)
x + 2x = 9
É verdadeira para x = 3

25. Cap3 - Equações
Sentenças Matemáticas expressas por uma igualdade
Cada uma dessas sentenças matemáticas exprime uma igualdade de
expressões chamadas membros da igualdade.
2 + 5 + 7 = 10 + 4
1° Membro 2° Membro
1° Prato 2° Prato

26. Cap3 - Equações
Sentenças Matemáticas expressas por uma igualdade
1° Membro 2° Membro
Veja os demais e outros exemplos:
a + 4 = 6
y + 3 = 10
1° Membro 2° Membro
x + 2x = 9
1° Membro 2° Membro
3x + 2 = x – 1
1° Membro 2° Membro
1° Membro 2° Membro
5a = b + 2a

27. Cap3 - Equações
EQUAÇÕES
A primeira sentença matemática apresenta apenas números. Por isso
é chamada de sentença matemática.
As outras três sentenças matemáticas são igualdades que
apresentam, além de números, letras. Essas sentenças são exemplos
de EQUAÇÕES
y + 3 = 10
1° Membro 2° Membro

28. Cap3 - Equações
EQUAÇÕES é toda sentença matemática com letras expressa por
uma igualdade. As letras da equação representam números
desconhecidos e são chamados de INCÓGNITA.
Não é uma equação,
Porque não tem
incógnita!!!
EQUAÇÕES

29. Cap3 - Equações
Bianchini – Pág 96



×
×
×

×

23

30. Cap3 - Equações
EXPRESSAR DADOS DE UMA PROBLEMA POR
MEIO DE UMA EQUAÇÃO
Esse procedimento facilita a resolução do problema.
1) Vamos descobrir um número desconhecido:
A soma do dobro de um número com 7 é igual a 15. Qual é esse
número?
Representando esse número por x, temos:
2x + 7 = 15
O dobro do número

31. Cap3 - Equações
EXPRESSAR DADOS DE UMA PROBLEMA POR
MEIO DE UMA EQUAÇÃO
2) Um ciclista desistiu da competição ao completar do percurso
total. Se ele tivesse corrido mais 2 quilômetros, teria cumprido do
percurso total. Qual a sentença matemática traduz, algebricamente, o
problema?
Representando o percurso total por y, temos:
4
1
3
1
yy
3
1
2
4
1
=+

32. Cap3 - Equações
RAIZ DE UMA EQUAÇÃO
A incógnita de uma equação pode assumir diversos valores, mas
apenas para alguns desses valores a sentença é verdadeira.
Num dos exemplos dados temos:
Neste caso, podemos dizer que o número 3 é a raiz da equação 2x +
x = 9

33. Cap3 - Equações
RAIZ DE UMA EQUAÇÃO
Esse procedimento de substituição da incógnita (letra) por
um número serve para verificar se esse número é ou não
raiz da equação.
Veja mais exemplos:
1) Vamos verificar se o número – 1 é raiz da equação 8x + 3 = – 5
8x + 3 = – 5
8. (– 1) + 3 = – 5
– 8 + 3 = – 5
– 5 = – 5 (verdadeira)
x é a incógnita da
equaçãoLogo, – 1 é a raiz da equação
8x + 3 = 5

34. Cap3 - Equações
RAIZ DE UMA EQUAÇÃO
2) O número – 3 é raiz da equação x2
– 2 = x + 18 ?
x2
– 2 = x + 18
(– 3 )2
– 2 = – 3 + 18 Substituindo x por – 3
9 – 2 = 15
7 = 15 (Sentença Falsa)
Logo, – 3 NÃO é a raiz da equação x2
– 2 = x + 18

35. Cap3 - Equações
SOLUÇÃO (RAIZ) DE UMA EQUAÇÃO
Bianchini Pág 97
Sim
Não Não
4x – 21 = x + 5
4. 2 – 21 = 2 + 5
8 – 21 = 7
– 13 = 7 (Sentença Falsa)
2 não é raiz da equação
4x – 21 = x + 5
Sim
28
30

36. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
Para resolver um equação, devemos saber quais valores a incógnita pode
assumir e quais valores tornam a sentença verdadeira.
Vamos analisar três sentenças:
1) “Um número natural par elevado ao quadrado e somado com 5 dá 21.”
x2
+ 5 = 21(0, 2, 4, 6, 8, ...) Conjunto Universo
U = {0, 2, 4, 6, 8, ...}

37. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
1) “Um número natural par elevado ao quadrado e somado com 5 dá 21.”
x2
+ 5 = 21
Observe que os – 4 e 4 tornam a equação x2
+ 5 = 21 verdadeira
No entanto, o conjunto universo é número natural par. Portanto a solução
da equação x2
+ 5 = 21 é o número
Conjunto Universo
U = {0, 2, 4, 6, 8, ...}
Para x = – 4, temos:
(– 4)2
+ 5 = 21
16 + 5 = 21
(verdadeira)
Para x = 4, temos:
42
+ 5 = 21
16 + 5 = 21
(verdadeira)
4

38. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
2) “Um número inteiro elevado ao quadrado e somado com 5 dá 21.”
x2
+ 5 = 21
Conjunto Universo U = {..., – 5, – 4, – 3, –2, – 1, 0 , 1, 2, 3, 4, 5, ...}
U = Z
As raízes da equação são – 4 e 4
Como ambas pertencem ao conjunto universo, a solução é – 4 e 4.

39. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
3) “Um número natural ímpar elevado ao quadrado e somado com 5 dá
21.”
x2
+ 5 = 21
Conjunto Universo U = {1, 3, 5, 7, 9, 11,...}
As raízes da equação são – 4 e 4
Assim, essa equação NÃO tem solução no conjunto universo dado

40. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
Bianchini Pág 99
34

41. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
Bianchini Pág 99
Equação dada:
Conjunto Universo: U = {2, 4, 6, 8, ...}
Solução ou raiz da equação: 6
3
2
=
y
34

42. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
Bianchini Pág 99
Equação dada:
Conjunto Universo: U = Z
Solução ou raiz da equação: – 3 ou 3
3=a
34

43. Cap3 - Equações
CONJUNTO UNIVERSO E SOLUÇÃO DE UMA
EQUAÇÃO
Bianchini Pág 99
Equação dada:
Conjunto Universo: U = N
Solução ou raiz da equação: A equação não tem solução
3
2
=
−
x
34

44. Cap3 - Equações
EQUAÇÕES DO 1° GRAU COM UMA INCÓGNITA
Considere as seguintes equações:
• 2x + 7 = 5 incógnita: x expoente: 1
• 3x + 2 = x – 3 incógnita: x expoente: 1
• 5x2
– 8x + 7 = 0 incógnita: x expoente: 2
• x + y = 0 incógnitas: x e y expoente: 1
As duas primeiras equações têm uma só incógnita (a letra x ) apenas com
expoente 1.
Elas são exemplos do que chamamos de
EQUAÇÕES DO 1° GRAU COM UMA INCÓGNITA

45. Cap3 - Equações
EQUAÇÕES DO 1° GRAU COM UMA INCÓGNITA
Bianchini Pág 100
35

46. Cap3 - Equações
EQUAÇÕES EQUIVALENTES
Um número pode ser representado de diferentes formas.
Por exemplo, representando o número 9 de diferentes maneiras:
A maneira mais simples de todas é, sem dúvida, 9.
Fato semelhante ocorre com as equações, veja a seguir
32
23
+ 1 52
– 42
18:2 6 + 3 10 – 1

47. Cap3 - Equações
EQUAÇÕES EQUIVALENTES
Algumas equações têm a mesma solução, mas estão expressas de forma
diferente.
Observe as equações, sendo U = Q
x + 3 = 10 raiz ou solução: 7
x = 10 – 3 raiz ou solução: 7
x = 7 raiz ou solução: 7

48. Cap3 - Equações
EQUAÇÕES EQUIVALENTES
Podemos representar essa
situação pela equação:
3x + 2 = 8
Retirando 2 pesos de 1kg de
cada prato a balança continua em
equilíbrio.
3x = 6
Deixando em cada prato a
terça parte do que ele tem a
balança continua em equilíbrio.
x = 2

49. Cap3 - Equações
EQUAÇÕES EQUIVALENTES
3x + 2 = 8
3x = 6
x = 2
Como 2 é solução das três equações, dizemos que elas são equações
equivalentes

50. Cap3 - Equações
RESOLUÇÃO DE EQUAÇÕES
1ª propriedade
2ª Propriedade
Equacionando problemas

51. Cap3 - Equações
RESOLVENDO EQUAÇÕES COM PARENTESES
1) Paula escreveu um número em seu caderno e fez o mesmo no caderno
de Joana. Depois Paula somou 1 a esse número, multiplicou o resultado
por 4 e somou 18. Joana somou 2, multiplicou o resultado por 5 e
subtraiu 3.
Paula e Joana obtiveram o mesmo resultado. Qual foi o número escrito
inicialmente por Paula?
Representando o número escrito por x, temos:
4(x + 1) + 18 = 5 (x + 2) – 3
Paula:
número x
somou 1 x + 1
Multiplicou por 4 4(x + 1)
somou 18 4(x + 1) + 18
Joana
número x
Somou 2 x + 2
Multiplicou por 5 5(x + 2)
somou 3 5(x + 2) – 3

52. Cap3 - Equações
RESOLVENDO EQUAÇÕES COM PARENTESES
Qual foi o número escrito inicialmente por Paula?
4(x + 1) + 18 = 5 (x + 2) – 3
Eliminamos os parênteses, aplicando a propriedade distributiva da
multiplicação, e continuamos a resolução.
4(x + 1) + 18 = 5 (x + 2) – 3
4x + 4 + 18 = 5x + 10 – 3
4x + 22 = 5x + 7
4x – 5x = 7 – 22
– x = – 15 (– 1)
x = 15
Logo, o número escrito foi 15

53. Cap3 - Equações
RESOLUÇÃO DE PROBLEMAS DE GEOMETRIA
USANDO EQUAÇÕES
Fábio cercou seu terreno com 92 m de tela de arame. Se o terreno tem a
forma de um quadrado, qual é a área do terreno?
1) Devemos encontrar a medida do lado o terreno (quadrado) através de
uma equação que relacione o perímetro do terreno.
Portanto, o terreno tem 23 m de comprimento e 23 m de largura
Portanto, a área do terreno é 529 m2
.
Terreno x
x
x + x + x + x = 92
4x = 92
x = 92_
4
x = 23
Para calcular a área do terreno, temos:
A = x.x
A = 23. 23
A = 232
A = 529

54. Cap3 - Equações
Bianchini Pág 111
41

55. Cap3 - Equações
RESOLVENDO EQUAÇÕES COM FRAÇÕES
Eliminando Denominadores
1) Todo início de mês, João separa a metade de seu salário para pagar o
aluguel, contas de água, luz etc., e mais dois quintos de seu salário para
os gastos com alimentação e transporte. Sobram R$ 160,00 para outras
despesas. Qual é o salário de João?
Salário de João
Metade do salário de João
Dois quintos do salário de João
de ou5
2
x
x
5
2x
2
x
160
5
2
2
++=
xx
x

56. Cap3 - Equações
RESOLVENDO EQUAÇÕES COM FRAÇÕES
Eliminando Denominadores
1) Todo início de mês, João separa a metade de seu salário para pagar o
aluguel, contas de água, luz etc., e mais dois quintos de seu salário para
os gastos com alimentação e transporte. Sobram R$ 160,00 para outras
despesas. Qual é o salário de João?
Multiplicamos todos dois membros da equação por um múltiplo comum
dos denominadores, ou seja, mmc (2,5) = 10
Portanto, João recebe R$ 1.600,00 por mês.
160
5
2
2
++=
xx
x
⋅





++=⋅ 160
5
2
2
xx
x10 10
=x10
16004510 ++= xxx
1600910 += xx
1600910 =− xx
1600=x
=⋅10
2
x
x5
x5
x4=⋅10
5
2x
x4+
10160⋅ 1600=
1600+

57. Cap3 - Equações
RESOLVENDO EQUAÇÕES COM FRAÇÕES
Eliminando Denominadores
2) Resolva o problema que a professora está propondo.
Resolução no quadro!!!

58. Cap3 - Equações
Bianchini Pág
Eliminando Denominadores
2) Resolva o problema que a professora está propondo.
Resolução no quadro!!!