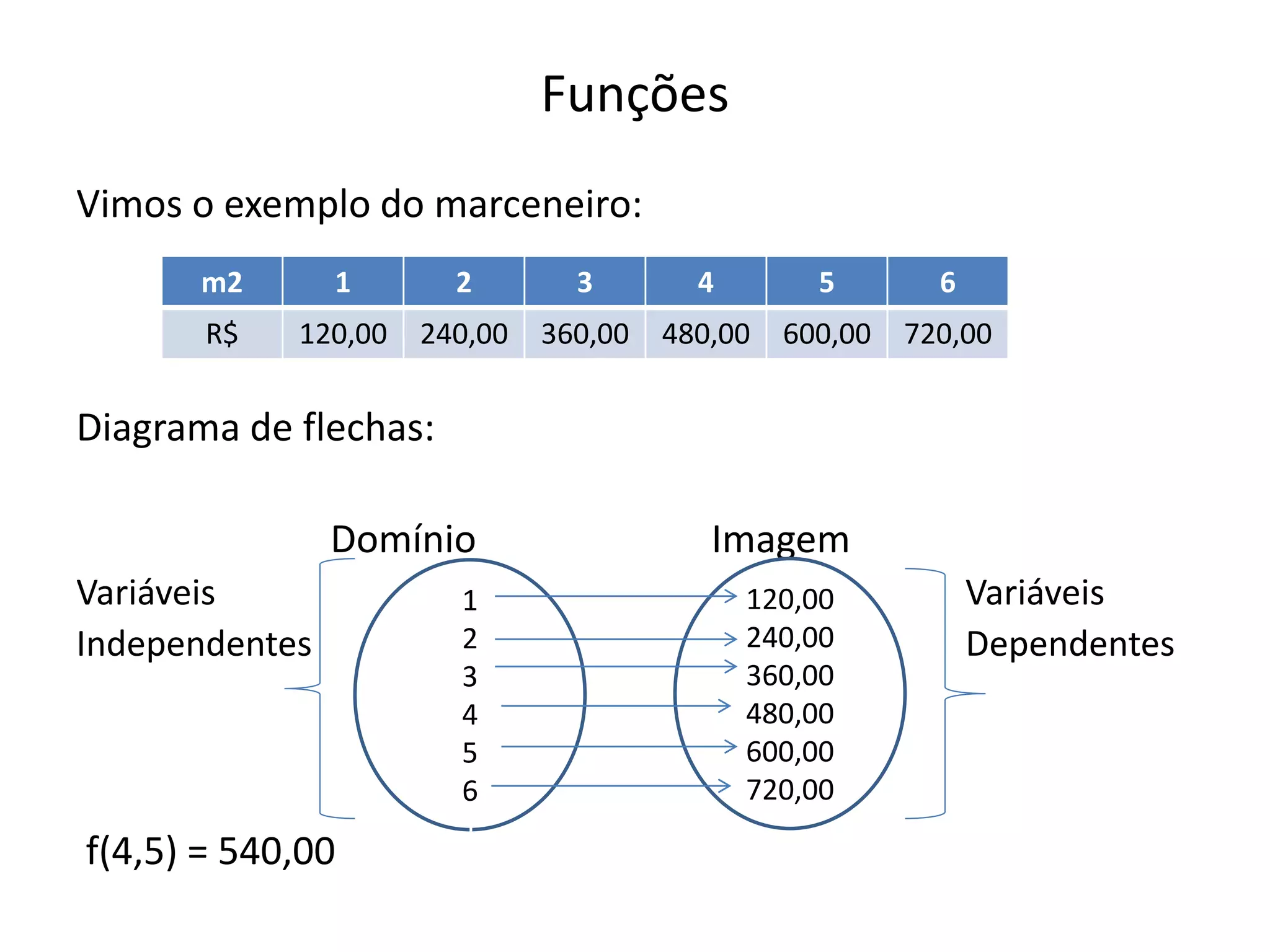
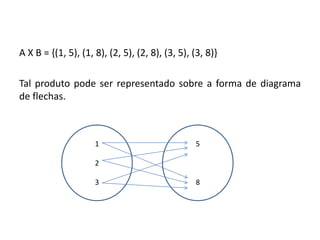
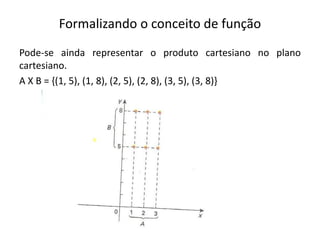
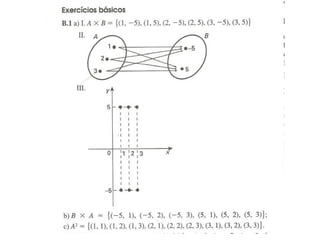
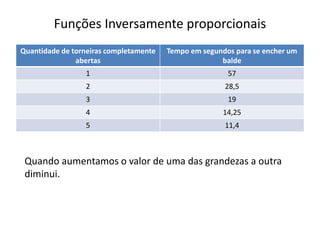
1) O documento discute funções matemáticas, incluindo definições, exemplos e tipos de funções como direta e inversamente proporcionais. 2) Apresenta o conceito formal de função usando produto cartesiano e mapeamento de conjuntos. 3) Fornece exemplos de grandezas que variam diretamente ou inversamente em função de outras grandezas.

1. Funções
Vimos o exemplo do marceneiro:
Diagrama de flechas:
Domínio Imagem
Variáveis Variáveis
Independentes Dependentes
f(4,5) = 540,00
m2 1 2 3 4 5 6
R$ 120,00 240,00 360,00 480,00 600,00 720,00
1
2
3
4
5
6
1
2
3
120,00
240,00
360,00
480,00
600,00
720,00

2. Funções
Definição de função: Em matemática, função significa uma
correspondência entre dois ou mais conjuntos, ou seja, função é
quando uma coisa muda, porque alguma outra coisa mudou
também.

3. Funções
Palavras mágicas
Estamos trabalhando com grandezas
Diretamente proporcionais
Inversamente proporcionais
Conjunto domínio
Conjunto imagem
Função Crescente e Decrescente
Representação no plano cartesiano

4. Funções
No caso da tabela do serralheiro x e y são duas grandezas
diretamente proporcionais y/x é constante (K é uma constante),
nesse caso K = 120,00, temos uma proporção.
O aumento no valor de “x” acarreta um aumento no valor de “y”.
Quando o aumento no valor de “x” acarreta uma diminuição no
valor de “y”, dizemos que são inversamente proporcionais,
exemplo:

5. Funções
- Grandeza é tudo aquilo que pode variar, seja aumentando, seja
diminuindo.
- Duas grandezas x e y podem variar de modo interdependente
(uma depende da outra).
- Quando uma grandeza x varia, notamos que os valores de outra
grandeza y também varia.
- Cada valor de x corresponde a um e somente um valor de y,
então podemos dizer que y é função de x.
- X é a variável independente e y é a variável dependente.
- Não é uma função.
1
2
3
A
B
C

6. Funções Inversamente proporcionais
Quantidade de torneiras completamente
abertas
Tempo em segundos para se encher um
balde
1 57
2 28,5
3 19
4 14,25
5 11,4
Quando aumentamos o valor de uma das grandezas a outra
diminui.

7. Funções
A proporcionalidade direta exige mais do que um aumento
simultâneo nos valores de x e y, é preciso que a razão seja
constante.
Exercício:
a) A altura “a” de uma pessoa é diretamente proporcional a sua
idade “t”.
b) A massa “m” de uma pessoa é diretamente proporcional a
sua idade “t”.
c) O perímetro “p” de um quadrado é diretamente proporcional
ao seu lado “a”.
d) O comprimento “c” de uma circunferência é diretamente
proporcional ao seu diâmetro “d”

8. Formalizando o conceito de função
Produto cartesiano
Sejam A e B conjuntos diferentes do vazio. Chama-se produto
cartesiano de A por B, e indica-se por A x B, o conjunto cujos
elementos são todos os pares ordenados (x, y), tais que x Ɛ A e y
Ɛ B.
A x B = {(x, y)} x Ɛ A e Y Ɛ B
Exemplo:
Sendo A= {1, 2, 3} e B= {5,8}
A X B = {(1, 5), (1, 8), (2, 5), (2, 8), (3, 5), (3, 8)}

9. A X B = {(1, 5), (1, 8), (2, 5), (2, 8), (3, 5), (3, 8)}
Tal produto pode ser representado sobre a forma de diagrama
de flechas.
1
2
3
5
8

10. Formalizando o conceito de função
Pode-se ainda representar o produto cartesiano no plano
cartesiano.
A X B = {(1, 5), (1, 8), (2, 5), (2, 8), (3, 5), (3, 8)}

11. Exercícios

12. Exercícios

13. Exercícios

14. Exercícios