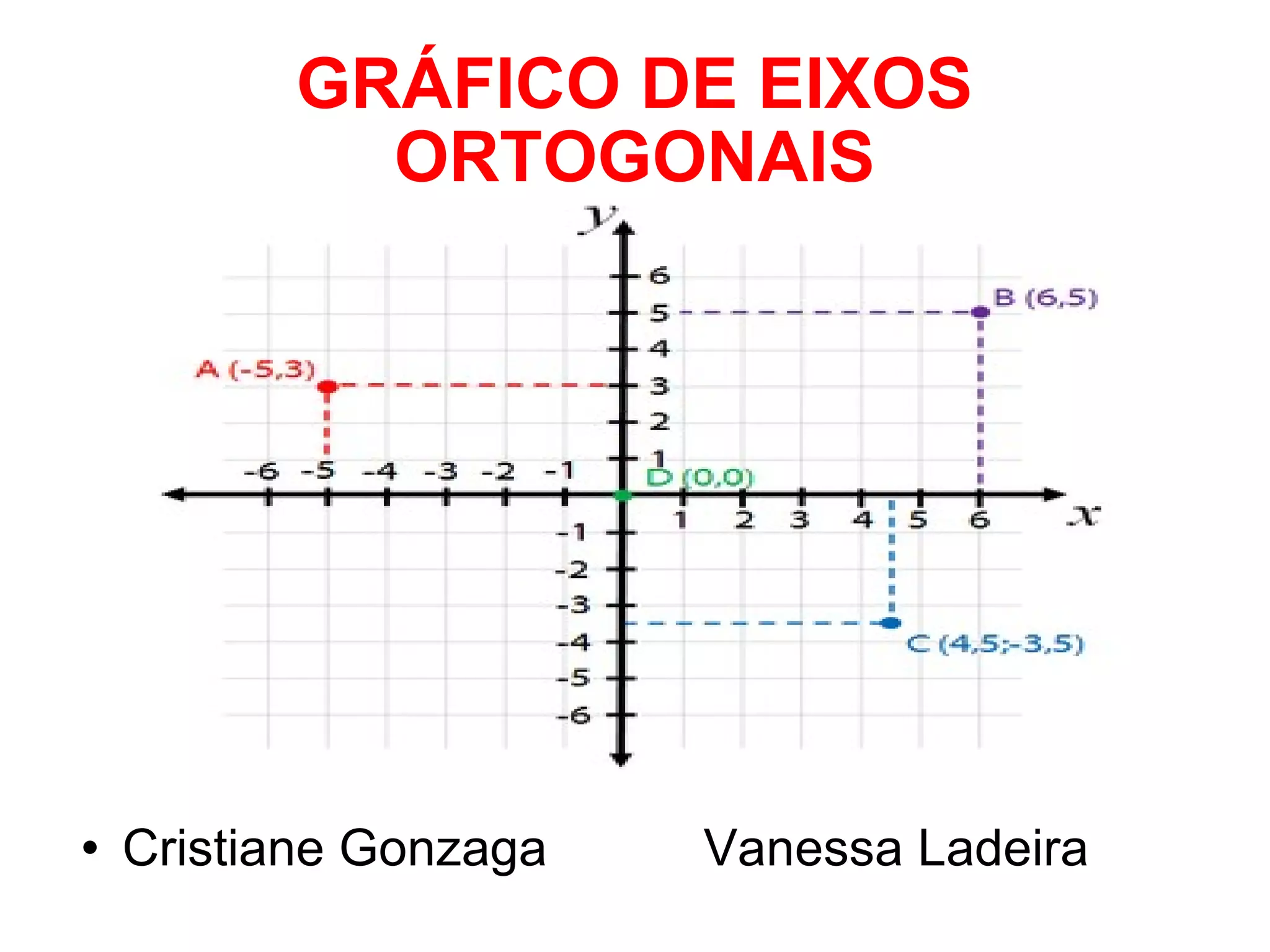
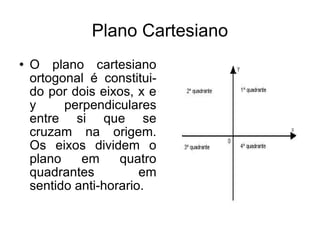
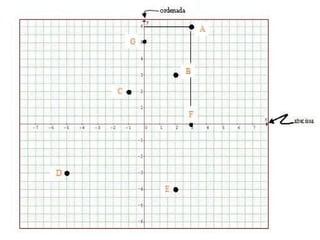
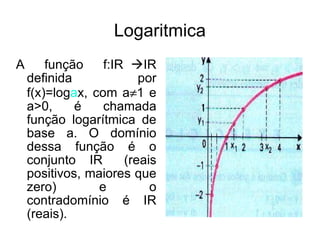
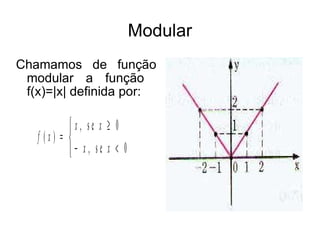
O documento descreve os conceitos básicos do plano cartesiano, incluindo os eixos x e y, quadrantes, pontos no plano representados por pares ordenados (x, y), e exemplos de pontos. Também define vários tipos de funções gráficas, como funções afim, quadrática, exponencial, logarítmica e modular.

1. GRÁFICO DE EIXOS ORTOGONAIS Cristiane Gonzaga Vanessa Ladeira

2. Plano Cartesiano O plano cartesiano ortogonal é constitui-do por dois eixos, x e y perpendiculares entre si que se cruzam na origem. Os eixos dividem o plano em quatro quadrantes em sentido anti-horario.

3. O Ponto no Plano Cada ponto do plano cartesiano é formado por um par ordenado P (x , y ), onde x: abscissa e y: ordenada.

4. Exemplos Marcamos alguns pontos no plano como exemplo: A(3,6), B(2,3), C(-1,2), D(-5,-3), E(2,-4), F(3,0), G(0,5). Marcando o ponto A(3,6) 1°: localiza-se o ponto 3 no eixo das abscissas 2°: localiza-se o ponto 6 no eixo das ordenadas 3°: Traçar a reta perpendicular aos eixos, o encontro delas será o local do ponto.

6. Gráficos de funções Chama-se função polinomial do 1º grau , ou função afim , a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a diferente 0.

7. Quadrática Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax 2 + bx + c , onde a, b e c são números reais e a 0.

8. Exponencial Chamamos de funções exponenciais aquelas nas quais temos a variável aparecendo em expoente. A função f:IR  IR + definida por f(x)=a x , com a  IR + e a  1, é chamada função exponencial de base a. O domínio dessa função é o conjunto IR (reais) e o contradomínio é IR + (reais positivos, maiores que zero).

9. Logaritmica A função f:IR +  IR definida por f(x)=log a x, com a  1 e a>0, é chamada função logarítmica de base a. O domínio dessa função é o conjunto IR + (reais positivos, maiores que zero) e o contradomínio é IR (reais).

10. Modular Chamamos de função modular a função f(x)=|x| definida por:

11. Referencial http://pt.wikipedia.org/wiki/Sistema_de_coordenadas_cartesiano lugli.org/wp-content/uploads/2008/02/01o_plano_cartesiano.pdf http://www.brasilescola.com/matematica/plano-cartesiano.htm http://somatematica.com.br/emedio/funcao1/funcao3.