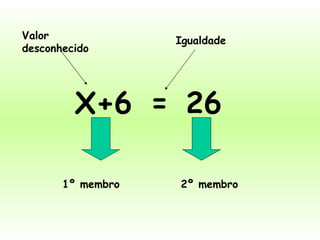
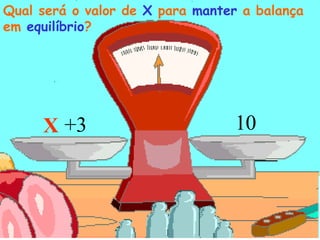
O documento apresenta definições e exemplos de equações do 1o grau. Explica que uma equação do 1o grau possui uma variável, um sinal de igualdade e expressões à esquerda e direita da igualdade. Apresenta também exemplos de como traduzir problemas matemáticos para a linguagem algébrica de equações.

1. Equações x +2 = -20 x + y = 15 x² + 3x -12 = 0 a + 5 = 8 - 5a

2. Equações do 1º Grau *Definição: É uma Sentença matemática aberta que expressa uma igualdade.

3. Equação do 1º grau Chamamos equação do 1º grau na incógnita X a toda equação que pode ser escrita na forma a . X + b = 0 , onde a é diferente de 0. a . X + b = 0 ( a e b são números reais e a é diferente de 0 )

4. Uma ou mais letras indicando valores desconhecidos, que são denominadas variáveis ou incognitas ; Um sinal de igualdade, denotado por = Uma expressão à esquerda da igualdade, denominada primeiro membro ou membro da esquerda; Uma expressão à direita da igualdade, denominada segundo membro ou membro da direita. Podemos ver que toda equação tem:

5. X+6 = 26 Valor desconhecido 2º membro Igualdade 1º membro

6. X 10 Qual será o valor de X para manter a balança em equilíbrio ? +3

7. x 10 Qual será o valor de X para manter a balança em equilíbrio ? +3 7

8. 10 +3 11 Observe que o valor de X for um número maior que 7 a balança desequilibra.

9. 10 +3 5 Observe que o valor de X for um número menor que 7 a balança desequilibra.

10. Traduzindo para linguagem matemática

11. O dobro de x O dobro de um número adicionado de 4 O triplo de um número O quadrado de a subtraído de 6 O cubo de a mais o dobro de x Vamos exercitar Um número adicionado de seu triplo O quíntuplo de a subtraído do sêxtuplo de y Um número adicionado de outro número

12. Traduzindo problemas para linguagem matemática

13. Exemplos: 1) A soma das idades de André e Carlos é 22 anos . Descubra as idades de cada um deles, sabendo-se que André é 4 anos mais novo do que Carlos.

14. Solução: Primeiro passamos o problema para a linguagem matemática . Vamos tomar a letra para a idade de Carlos e a letra para a idade de André . Agora vamos escrever o problema na linguagem matemática usando esta letra

15. c + a = 22 c + (c - 4) = 22 2c - 4 = 22 2c - 4 + 4 = 22 + 4 2c = 26 c = 13 Resposta : Carlos tem 13 anos e André tem 13-4=9 anos . Resolução

16. 2) A população de uma cidade A é o triplo da população da cidade B. Se as duas cidades juntas têm uma população de 100.000 habitantes, quantos habitantes tem a cidade B?

17. Solução : Identificaremos a população da cidade A com a letra a e a população da cidade B com a letra b. Assumiremos que a=3b. Dessa forma, poderemos escrever: Primeiro passamos o problema para a linguagem matemática. Agora escreva e equação que representa o problema

18. a + b = 100.000 3b + b = 100.000 4b = 100.000 b = 25.000 Resposta: Como a=3b, então a população de A corresponde a: a=3×25.000=75.000 habitantes. Resolução