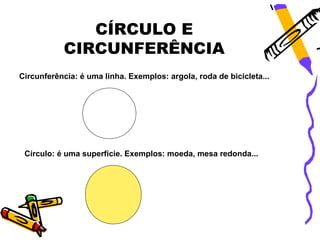
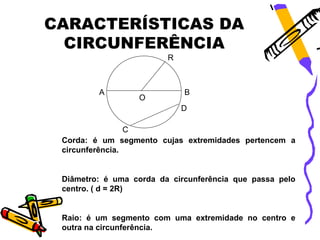
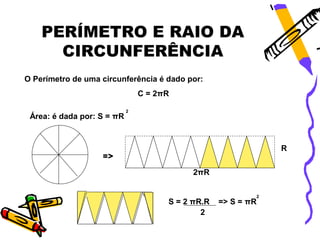
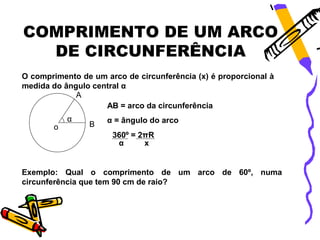
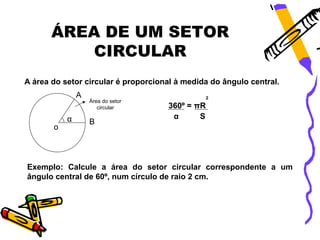
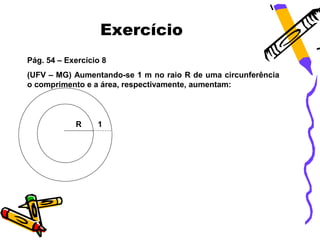
O documento explica as características de círculos e circunferências, incluindo que uma circunferência é uma linha em forma de círculo enquanto um círculo é uma superfície plana. Ele também define termos como raio, diâmetro e corda e fornece fórmulas para calcular o perímetro, área, comprimento de arcos e áreas de setores circulares. Exemplos ilustram como aplicar essas fórmulas para cálculos.

1. CÍRCULO E
CIRCUNFERÊNCIA
Circunferência: é uma linha. Exemplos: argola, roda de bicicleta...
Círculo: é uma superfície. Exemplos: moeda, mesa redonda...

2. CARACTERÍSTICAS DA
CIRCUNFERÊNCIA
R
A B
O
D
C
Corda: é um segmento cujas extremidades pertencem a
circunferência.
Diâmetro: é uma corda da circunferência que passa pelo
centro. ( d = 2R)
Raio: é um segmento com uma extremidade no centro e
outra na circunferência.

3. PERÍMETRO E RAIO DA
CIRCUNFERÊNCIA
O Perímetro de uma circunferência é dado por:
C = 2πR
2
Área: é dada por: S = πR
R
=>
2πR
2
S = 2 πR.R => S = πR
2

4. COMPRIMENTO DE UM ARCO
DE CIRCUNFERÊNCIA
O comprimento de um arco de circunferência (x) é proporcional à
medida do ângulo central α
A
AB = arco da circunferência
α α = ângulo do arco
o B
360º = 2πR
α x
Exemplo: Qual o comprimento de um arco de 60º, numa
circunferência que tem 90 cm de raio?

5. ÁREA DE UM SETOR
CIRCULAR
A área do setor circular é proporcional à medida do ângulo central.
A 2
Área do setor
circular 360º = πR
α α S
B
o
Exemplo: Calcule a área do setor circular correspondente a um
ângulo central de 60º, num círculo de raio 2 cm.

6. Exercício
Pág. 54 – Exercício 8
(UFV – MG) Aumentando-se 1 m no raio R de uma circunferência
o comprimento e a área, respectivamente, aumentam:
R 1

7. Exercício
Pág. 53 – Exercício 2
(ESPM – SP) Uma circunferência está inscrita em um quadrado cuja
diagonal mede 20 cm. O comprimento da circunferência é:

8. Trabalho
Pág. 36 – Exercícios 01 ao 06
Pág. 43 – Exercícios 01 ao 06
Pág. 53 – Exercícios 01 ao 06
Entregar no dia da prova