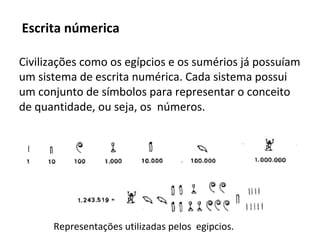
O documento discute sistemas de numeração, incluindo conceitos como número, numeral e algarismo. Apresenta sistemas numéricos posicionais e não posicionais, destacando o sistema binário usado em computadores. Explica as bases numéricas e conversões entre sistemas como decimal, binário e hexadecimal.

1. Sistemas de
numeração
Prof. Sérgio Souza Costa
Notas de aula em: https://sites.google.
com/site/profsergiocosta/projects/eacit/notas-de-
aula/sistemasdenumeracao

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
https://twitter.com/profsergiocosta
http://gplus.to/sergiosozuzacosta
http://www.slideshare.net/skosta/presentations?order=popular
http://br.linkedin.com/pub/s%C3%A9rgio-souza-costa/20/9b0/ba9/

3. O que é um número ?

4. ?
Pedra (Calculus em latim)
As pedras foram um dos primeiros mecanismos
utilizados pelo homem para representar e controlar as
quantidades.

5. Civilizações como os egípcios e os sumérios já possuíam
um sistema de escrita numérica. Cada sistema possui
um conjunto de símbolos para representar o conceito
de quantidade, ou seja, os números.
Escrita númerica
Representações utilizadas pelos egípcios.

6. Três noções numéricas
básicas: número,
numeral e algarismo

7. Número é a ideia de quantidade que nos vem à
mente quando contamos, ordenamos e medimos.
Assim, estamos pensando em números quando:
● contamos as portas de um automóvel,
● enumeramos a posição de uma pessoa numa fila
ou
● medimos o peso de uma caixa.
Número

8. Numeral é toda representação de um número, seja ela escrita
ou falada. Algarismos (ou dígitos) é todo símbolo numérico que
usamos para formar os numerais escritos.
● Por exemplo, o número vinte e três pode ser representado
pelo numeral XXIII ( no sistema romano ), pelo numeral 23 (
no sistema indo-arábico ) e de muitas outras maneiras.
● No sistema indo-arábico, sua representação usou os
algarismos 2 e 3, e no sistema romano usou os algarismos X
e I. Além disso, um mesmo numeral, como 34, pode
representar números diferentes dependendo do sistema
numérico.
Numeral e algarismos

9. Numeral é toda representação de um número, seja ela escrita
ou falada. Algarismos (ou dígitos) é todo símbolo numérico que
usamos para formar os numerais escritos.
● Por exemplo, o número vinte e três pode ser representado
pelo numeral XXIII ( no sistema romano ), pelo numeral 23 (
no sistema indo-arábico ) e de muitas outras maneiras.
● No sistema indo-arábico, sua representação usou os
algarismos 2 e 3, e no sistema romano usou os algarismos X
e I. Além disso, um mesmo numeral, como 34, pode
representar números diferentes dependendo do sistema
numérico.
Numeral e algarismos
Algarismo é
também
referido como
digito.

10. Sistemas numéricos é todo conjunto de regras para a
produção sistemática de numerais e associa-los a números.
No caso de sistemas de numeração escrita, a produção dos
numerais é feita através de combinações de algarismos e
eventuais símbolos não numéricos ( como a vírgula no
sistema indo-arábico, ou vinculum no sistema romano etc ).
Sistemas numéricos

11. Sistemas numéricos é todo conjunto de regras para a
produção sistemática de numerais e associa-los a números.
No caso de sistemas de numeração escrita, a produção dos
numerais é feita através de combinações de algarismos e
eventuais símbolos não numéricos ( como a vírgula no
sistema indo-arábico, ou vinculum no sistema romano etc ).
Sistemas numéricos
Esta combinação pode
levar em conta ou não as
posições onde são
encontrados estes
símbolos, sendo
classificados em
posicionais ou não
posicionais
respectivamente.

12. Por exemplo, o principal sistema numérico utilizado pelos
romanos era não posicional. Este sistema era constituído por
7 algarismos diferente, cada um representando um valor fixo,
independente de sua posição relativa no número:
N = { I, V, X, L, C, D, M}
Indicando respectivamente os valores:
1, 5, 10, 50, 100, 500, 1000
Sistemas não posicional

13. Nesse sistema não há um símbolo representativo para o zero;
os números sao definidos da esquerda para direita, e seus
valores obtidos segundo uma regra simples:
● Cada algarismo colocado a direita de um maior é adicionado
a esse, por exemplo, VI representa o número seis.
● Cada algarismo colocado a esquerda de outro maior é
subtrai desse, por exemplo, IV representa o número quatro.
Sistemas não posicional

14. Nesse sistema não há um símbolo representativo para o zero;
os números sao definidos da esquerda para direita, e seus
valores obtidos segundo uma regra simples:
● Cada algarismo colocado a direita de um maior é adicionado
a esse, por exemplo, VI representa o número seis.
● Cada algarismo colocado a esquerda de outro maior é
subtrai desse, por exemplo, IV representa o número quatro.
Sistemas não posicional
Este sistema não foi
criado para efetuar
cálculos matemáticos,
tarefa extremamente
árdua de ser realizada
com este sistema.

15. Série Bits e Bytes - 01 - Os números e a
invenção do computador
http://www.youtube.com/watch?v=6rH00V0Bd6c

16. Em um sistema posicional o valor de cada algarismo de um número
diferente, conforme sua posição no número. Por exemplo, no
sistema decimal o numero representativo do valor 3433 é
constituído por 4 algarismos, onde 3 tem o mesmo valor absoluto.
O valor absoluto de cada algarismo é modificado por um peso
conforme sua posição:
343310
= 3* 1000 + 4 * 100 + 3 * 10 + 3
Observe que este peso tem como potencia 10i
para i = 0,1,2,3.
Então, podemos reescrever o numero da seguinte maneira:
343310
= 3* 103
+ 4 * 102
+ 3 * 101
+ 3 * 100
Sistema posicional

17. A base utilizada dependerá da quantidade de símbolos usada no
sistema numérico em questão. No caso do sistema decimal temos
10 símbolos, portanto sua base é 10:
0,1,2,3,4,5,6,7,8,9
A base 10 atualmente é a mais utilizada nas tarefas do dia a dia,
porém em alguns casos precisaremos usar outra base.
Sistema posicional (decimal)

18. De modo geral, em um sistema posicional de base B
teremos um conjunto S de algarismos:
S = {db-1
, db-2
, db-3
, .. d1
, d0
}
Assim cada número pode ser descrito por:
N= d(n-1)
* base(n-1)
+ d(n-2)
* base(n-2)
+...+d(0)
* base(0)
Sistema posicional (decimal)

19. Os microprocessadores dos computadores fazem aritméticas
usando a base 2, composta apenas por dois símbolos:
0, 1
Estes símbolos representam respectivamente ligado e desligado.
Os projetista de computadores observaram que a distinção entre
estes símbolos é muito mais confiável, do que se utilizasse
diferentes valores de tensão para tentar representar o sistema
decimal.
Sistema posicional (binário)

20. Os microprocessadores dos computadores fazem aritméticas
usando a base 2, composta apenas por dois símbolos:
0, 1
Estes símbolos representam respectivamente ligado e desligado.
Os projetista de computadores observaram que a distinção entre
estes símbolos é muito mais confiável, do que se utilizasse
diferentes valores de tensão para tentar representar o sistema
decimal.
Alguns dos primeiros computadores usavam o sistema decimal,
porém os circuitos eram mais complexos e menos confiáveis.
Sistema posicional (binário)

21. Os microprocessadores dos computadores fazem aritméticas
usando a base 2, composta apenas por dois símbolos:
0, 1
Estes símbolos representam respectivamente ligado e desligado.
Os projetista de computadores observaram que a distinção entre
estes símbolos é muito mais confiável, do que se utilizasse
diferentes valores de tensão para tentar representar o sistema
decimal.
Alguns dos primeiros computadores usavam o sistema decimal,
porém os circuitos eram mais complexos e menos confiáveis.
Sistema posicional (binário)
Como o sistema binário
possuem menos símbolos, é
necessário muito mais
algarismos do que no sistema
decimal para representar o
mesmo número. Porém, a
confiabilidade alcançada com
os números binários compensa
essa diferença.

22. Onde, d representa o dígito considerado e n representa
a quantidade de dígitos do número. Por exemplo, para
a base 2 temos:
S = {0,1}
O numero 1110
é representado como:
10112
= 1 * 23
+ 0 * 22
+ 1 * 21
+ 1 * 20
= 8 + 0 + 2 + 1 = 11
Sistema posicional (binário)

23. ● Uma palavra de N bits pode representar 2N
valores
● Exemplo
● Uma palavra de 3 bits pode representar 23
valores, ou seja,
8 valores (de 0 a 7)
● 000, 001, 010, 011, 100, 101, 110, 111
● Uma palavra de 1 byte pode representar 28
valores, ou
seja, 256 valores (de 0 a 255).
Sistema posicional (binário)

24. 0 0
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
16 10000
17 10001
18 10010
19 10011
20 10100
Decimal e binário

25. ● A conversão de binário para decimal é feita utilizado-se a
mesma fórmula genérica de decomposição de um número,
só que utilizando a base 2
● Por exemplo: Qual o valor decimal correspondente ao
número 10011?
1 * 24
+ 0 * 23
+ 0 * 22
+ 1 * 21
+ 1 * 20
=
16 + 0 + 0 + 2 + 1 = 19
● Exemplo 2: Qual o valor decimal correspondente ao número
101100?
1 * 25
+ 0 * 24
+ 1 * 23
+ 1 * 22
+ 0 * 21
+ 0 * 20
=
32 + 0 + 8 + 4 + 0 + 0 = 44
Conversão binário decimal

26. ● Converta em decimal os seguintes números binários
● 100110
● 1010111
● 0101011
● 1010101
● 11111000
Exercitando ...

27. ● A conversão de um número decimal para um número binário
é feita pela divisão do número decimal pela base destino
sucessivamente
● O número binário é o resto de cada divisão
● Exemplo: 49(10)
= ?(2)
49 ÷ 2 = 24 –> resto 1
24 ÷ 2 = 12 –> resto 0
12 ÷ 2 = 6 –> resto 0
6 ÷ 2 = 3 –> resto 0
3 ÷ 2 = 1 –> resto 1
1 ÷ 2 = 0 –> resto 1
110001
Conversão decimal binário

28. ● Exemplo 2: 67(10)
= ?(2)
67 ÷ 2 = 33 – resto 1
33 ÷ 2 = 16 – resto 1
16 ÷ 2 = 8 – resto 0
8 ÷ 2 = 4 – resto 0
4 ÷ 2 = 2 – resto 0
2 ÷ 2 = 1 – resto 0
1 ÷ 2 = 0 – resto 1
1000011
Conversão decimal binário

29. ● Converta
● 123(10)
= ?(2)
● 4567(10)
= ?(2)
● 5892(10)
= ?(2)
● 1101101(2)
= ?(10)
● 10001110(2)
= ?(10)
Exercitando ...

30. ● Possui 16 dígitos: 1,..., 9, A, B, C, D, E, F
● A = 10 ; B = 11 ; C = 12 ; D = 13; E = 14 ; F = 15
● A transformação para decimal é feita de
maneira análoga ao já apresentado. Exemplos:
● (1B)16
= 1x161
+ 11x160
= 16 + 11 = 2710
● (EC)16
= 14x161
+ 12x160
= 224 + 12 = 23610
● (3AF)16
= 3x162
+ 10x161
+ 15x160
= 768 + 160 + 15
= 92310
Sistema hexadecimal

31. ● Para converter um número decimal deve-se dividir o
valor sucessivamente por 16
● Exemplos:
● 12510
=?16
● 125 ÷ 16 = 7 → Resto 13 = D
● 12510
=7D
● 345610
=?16
● 3456 ÷ 16 = 216 → Resto 0
● 216 ÷ 16 = 13 → Resto 8
● 345610
=D8016
Conversão decimal hexadecimal

32. Para os computadores, o sistema binário se mostrou muito melhor que o
sistema decimal. Porém, para nós, seres humanos esta representação é
muito mais complexa, pois os números têm muitos algarismos. Assim, em
computação é comum usar comum duas outras bases alternativas, cuja
conversão para a base 2 é mais direta.
● O sistema octal (base 8) e hexadecimal (base 16). A conversão entre
estes sistemas e o binário é direto por que estas bases são potência de
dois. Por exemplo, o sistema octal que é composto por 8 simbolos
pode ser representados por 3 algarismo binarios, ou seja, 23
.
● Com mais um algarismo, podemos representar os 16 símbolos do
sistema hexadecimal:
Conversão Hexadecimal - Binário

33. ● 0000 – 0
● 0001 – 1
● 0010 – 2
● 0011 – 3
● 0100 – 4
● 0101 – 5
● 0110 – 6
● 0111 – 7
● 1000 – 8
● 1001 – 9
● 1010 – A
● 1011 – B
● 1100 – C
● 1101 – D
● 1110 – E
● 1111 – F
Conversão Hexadecimal - Binário

34. A partir da tabela do slide anterior podemos facilmente
converter um numero de Hexadecimal para binário. Por
exemplo, o número 3CF116 na base 2:
Ou seja, o numero 3CF11616
é representado por
0011110011110001000101102
. A mesma abordagem
pode ser usada para converter um número binário
para o equivalente em Hexadecimal ou Octal.
Conversão Hexadecimal - Binário

35. ● Exemplos
● AB16
= 101010112
● 4CF16
= 0100110011112
● FE6916
= 11111110011010012
● 1010 1111 01102
= AF616
● 1010101010101012
= 555516
● 1011111011110111012
= 2FBDD16
Conversão Hexadecimal - Binário

36. No sistema octal existem 8 dígitos: 0 – 7
Sistema octal utiliza o mesmo procedimento de conversão do
hexa → binário.
000 = 0
001 = 1
010 = 2
011 = 3
100 = 4
101 = 5
110 = 6
111 = 7
Sistema octal

37. ● Exemplos de conversão
● 3248
= 0110101002
● 12348
=0010100111002
● 654378
= 1101011000111112
● 010111011012
= 13558
● 1101111110112
= 67738
● 10101011101110112
= 1256738
Sistema octal

38. ● Para converter da base octal para hexadecimal
e vice-versa utiliza-se o sistema binário como
intermediário
● Exemplos
● 2348
= 0100111002
= 9C16
● 45628
= 1001011100102
= 972 16
● 76568
= 1111101011102
= FAE 16
● F216
= 111100102
= 3628
● A8B16
= 1010100010112
= 52138
● F9C316
= 11111001110000112
= 1747038
Mais conversões

39. Exercício
Decimal Binário Octal Hexa
2345
1000110110101
FAE5
234517
10000111111011 21FB
2345112
AA34
67895
Complete a tabela a
seguir

40. Além das conversões, é necessário conhecer as operações
aritméticas em outras bases. As operações aritméticas em
sistemas posicionais é muito mais simples do que nos sistemas
não posicionais
A regra é a mesma independentemente da base. Lembrando que
a soma de 1 com 1 resulta em 10 (2 em decimal). Quando isso
ocorre, dizemos que “vai 1” para ser somado na próxima posição.
Por exemplo, somando os numeros 0100 e 0101 temos como
resultado 1001:
Operações aritméticas

41. ● Os sistemas numéricos foram uma das grandes
invenções da humanidade. Com os sistemas numéricos
os homens passaram ser capazes de representar
grandezas e realizar cálculos entre estas.
● Como o computador é uma maquina especializada em
realizar cálculos, a formalização dos sistema numéricos
foi de grande importância para a evolução da ciência
computação.
● Deste modo, a compreensão destes sistemas é
fundamental aos estudiosos destas áreas.
Conclusão