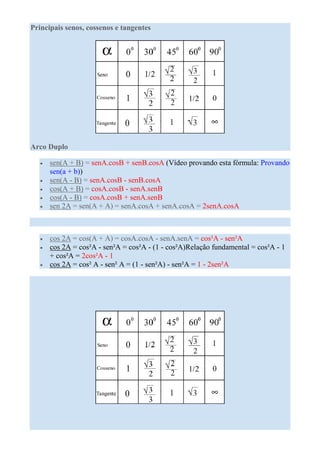
Este documento apresenta os conceitos básicos da trigonometria, incluindo definições de seno, cosseno e tangente em função dos catetos e hipotenusa de um triângulo retângulo. Também apresenta a relação fundamental da trigonometria e o ciclo trigonométrico.

1. BASE DA TRIGONOMETRIA
p = Hipotenusa(H);
q = Cateto Oposto à α(CO);
r = Cateto Adjacente à α(CA)
Trigonometria: Medida do triângulo(especialmente o triângulo retângulo)
Seno, cosseno, tangente, ...
• Seno α = CO/H = q/p
• Cosseno α = CA/H = r/p
• Tangente α = Seno/Cosseno = CO/CA = q/r
• Cossecante α = 1/seno = H/CO = p/q (inverso do seno)
• Secante α = 1/cosseno = H/CA = p/r (inverso do cosseno)
• Cotangente α = 1/tangente = Cosseno/Seno = CA/CO = r/q (inverso da
tangnte)
Relação Fundamental da Trigonometria:
AB = a;
BC = b;
AC = c.
sen² α + cos² α = 1

2. Prova :
seno α = a/b => a = b.sen α
cos α = c/b => c = b.cos α
a² + c² = b² => b².sen²α + b².cos²α = b² => 1.sen²α + 1.cos²α = 1(corta todos os "b²")
=>
sen²α + cos²α = 1
Ciclo trigonométrico
O ciclo mostra o seno, o cosseno e a yangente no plano cartesiano.
O eixo das abiscissas é o cosseno e o eixo das ordenadas é o seno e ainda tem o eixo
tangencial à circunferência que é a tangente.
O eixo é dividido em quadrantes
I - 1° quadrante
II - 2° quadrante
III - 3° quadrante
IV - 4° quadrante
Em I, o seno, o cosseno e a tangente são positivos;
Em II, o seno é positivo;
Em III, a tangente é positiva;
Em IV, o cosseno é positivo.
O ciclo trigonométrico é unitário, ou seja, do centro à circunferência é 1, porque o
maior seno e maior cosseno é igual à 1 e o menor seno e menor cosseno é igual à -1.

3. Principais senos, cossenos e tangentes
Arco Duplo
• sen(A + B) = senA.cosB + senB.cosA (Vídeo provando esta fórmula: Provando
sen(a + b))
• sen(A - B) = senA.cosB - senB.cosA
• cos(A + B) = cosA.cosB - senA.senB
• cos(A - B) = cosA.cosB + senA.senB
• sen 2A = sen(A + A) = senA.cosA + senA.cosA = 2senA.cosA
• cos 2A = cos(A + A) = cosA.cosA - senA.senA = cos²A - sen²A
• cos 2A = cos²A - sen²A = cos²A - (1 - cos²A)Relação fundamental = cos²A - 1
+ cos²A = 2cos²A - 1
• cos 2A = cos² A - sen² A = (1 - sen²A) - sen²A = 1 - 2sen²A

4. IIIIIIIIIIIIIIIIIIIIIIIQUESTÕESIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
01 - (Fuvest - modificada)Se α é um ângulo tal que 0 < α < π/2 e senα = a, então
tg(π - α) é igual a quanto?
α é menor que 90° graus então pertence ao primeiro quadrante.
π é 180°
então π - α está entre 90° e 180°, ou seja, segundo quadrante(figura).
Como tangente é seno sobre cosseno e o
seno de α é "a", a resposta terá um "a"
em cima.
Como a tangente no segundo quadrante é
negativa, a resposta será negativa.
Esta não é a figura da questão, então desconsiderem que o α seja o ângulo mostrado.
Imaginem o ângulo mostrado como (π - α)
O ângulo que a figura mostra pode ser π - α. A reta que sai do ponto "A" marca o
cosseno na reta x. Podemos chamar o cosseno de "m", por exemplo.
sen²α + cos² α = 1
a² + m² = 1
m² = 1 - a²
m = √1 - a²
tangente = seno/cosseno = a/m = a/√1 - a² = -a/√1 - a²
Resposta: -a .
√1 - a²

5. 02 - Considere a igualdade tgx = cotgx + [P.(2 - sec²x)/2tgx]. Qual é o valor de P,
para o qual a igualdade acima seja válida para todo x R, x ≠ 0 kπ/2, K inteiro.
tgx = cotgx + [P.(2 - sec²x)/2tgx]
tgx - cotgx = 2.P - sec²x.P
2tgx
tgx.2tgx - 1 .2tgx = 2.P - sec²x.P
tgx
2tg²x - 2 = 2.P - sec²x.P
2. sen²x - 2 = 2.P - 1 .P
cos²x cos²x
2.sen²x - 2cos²x = 2cos²x.P - P
cos²x
2(sen²x - cos²x) = P(2cos²x - 1)
2(sen²x - cos²x) = P(cos²x + cos²x - 1)
sen²α + cos²α = 1 => cos²α - 1 = -sen²α
2(sen²x - cos²x) = P(cos²x - sen²x)
P = 2 (sen²x - cos²x)
-1(sen²x - cos²x)
Resposta: P = -2
03 - Para representar os harmônicos emitidos pelos sons dos instrumenteos da
orquestra, usam-se funções trigonométricas. A expressão 2 sen²x + 2cos²x - 5
envolve estas funções e, para π < x < 3π/2, seu valor é:
2sen²x + 2cos²x - 5 =
2(sen²x + cos²x) - 5 =
2.1 - 5 =
2-5=
-3
Resposta: -3

6. 04 - Demonstre a identidade a seguir:
tg x + cotg x = sec x . cossec x
sen + cos = 1 . 1
cos sen cos sen
sen² + cos² = 1
sen.cos sen.cos
1 = 1
sen.cos sen.cos
sen.cos = 1
sen.cos
1=1
05 - Quanto é sen75°?
sen75° = sen (30 + 45) = sen30.cos45 + sen45.cos30
1 . √2 + √2 . √3
2 2 2 2
√2 + √6
4 4
√2 + √6
4
Resposta: √2 + √6
4
06 - Obtenha todos os pares (x, y) com x, y ∈ [0, 2π], tais que:
sen(x + y) + sen(x - y) = 1/2
sen x + cos y = 1
sen (x + y) = sen x . cos y + sen y . cos x
sen (x - y) = sen x . cos y - sen y . cos x
sen x . cos y + sen y . cos x + sen x . cos y - sen y . cos x = 1/2
sen x . cos y + sen y . cos x + sen x . cos y - sen y . cos x = 1/2
2 sen x . cos y = 1/2
sen x . cos y = 1/4
sen x + cos y = 1
sen x . cos y = 1/4
sen x = 1/2 = 30°
cos y = 1/2 = 60°
Resposta: (30°, 60°); (390°, 420°); ...

7. 07 - Se a medida de um arco, em graus, é igual a 128, sua medida em radianos é
igual a:
a) (π/4) - 17 Essa questão é super simples!
b) (54/15)π
É só fazer uma regra de três:
c) (64/45)π
d) (16/25)π 180 ----> π
e) (32/45)π 128 ----> x
180 . x = π . 128
x = π . 128/180
x = (32/45)π
Resposta: e) (32/45)π
08 - A tangente do ângulo 2x é dada em função da tangente de x pela seguinte
fórmula:
tg 2x = 2tg x/1 - tg²x
Calcule um valor aproximado da tangente do ângulo 22º 30'.
a) 0,22
b) 0,41
c) 0,50 Considere 22° 30' = x
d) 0,72 Portanto, 2x = 45°
e) 1,00
tg 2x = 2tg x/1 - tg²x
tg 45° = 2 . tg 22° 30'/1 - tg² 22° 30' tg 22° 30' = - 1 + √8/2
1 = 2 . tg 22° 30'/1 - tg² 22° 30' √8 é aproximadamente 2,82/2 = 1,41
0 = (2 . tg 22° 30'/1 - tg² 22° 30') - 1 1,41 - 1 = 0,41 = tg 22° 30'
0 = 2 . tg 22° 30' - 1 + tg² 22° 30'
tg² 22° 30' + 2 . tg 22° 30' - 1 = 0 --> Eq. Resposta: b)0,41
2° Grau
tg 22° 30' = x
x² + 2x - 1 = 0
/ = 4 + 4
/ = 8
x = - 2 +- √8
2
x' = -1 + √8
2
x'' = - 1 - √8 ---> tg 22° 30' é positiva
2

8. 09 - O desenvolvimento de 1 - tg² x para x ≠ nπ ± π/2, sendo n um inteiro
qualquer é:
1 + tg² x
a) sec² x - 1
b) sec² x + 1
c) sen² x - cos² x
d) cos² x - sen² x
e) tg² x
1 - sen² x
cos² x
1 + sen² x
cos² x
cos² x - sen² x
cos² x
cos² x + sen² x
cos² x
cos² x - sen² x
sen² x + cos² x = 1
cos² x - sen² x
Resposta: d) cos² x - sen² x
10 - Qual o valor da expressão abaixo?
(2 . sen4 20° - 2 . cos4 20°) . cossesc4 20°
3 - 3 . cotg4 20°
a) - 2/3
b) 2/3
c) 1/3
d) - 1/3
e) 0
(2 . sen4 20° - 2 . cos4 20°) . 1/sen4 20°
3 sen4 - 3 cos4 20°
sen4 20°
2 . sen4 20° - 2 . cos420°
3 sen4 20° - 3 cos4 20°
2 . (sen4 20° - cos420°)
3. (sen4 20° - cos4 20°)
2/3 Resposta: b)2/3