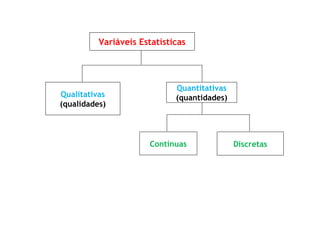
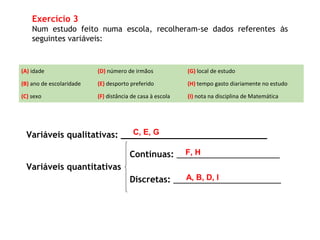
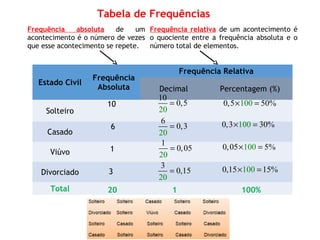
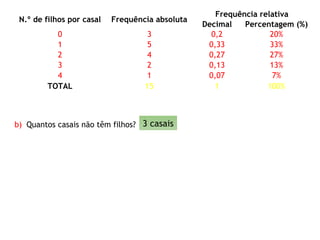
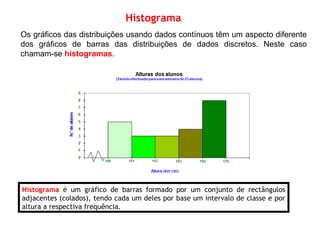
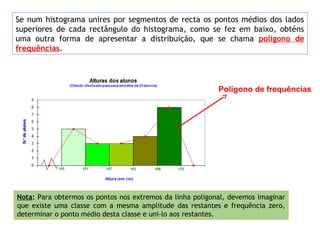
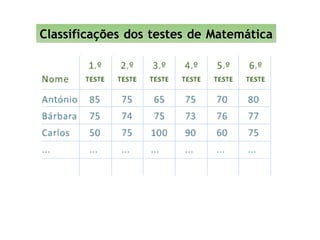
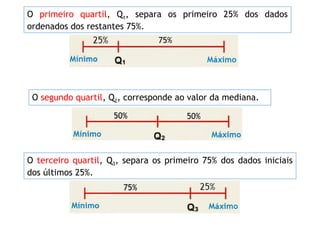
O documento discute a importância da estatística para entender dados e populações. A estatística é uma ferramenta matemática para organizar, analisar e interpretar conjuntos de dados de forma a extrair informações úteis. Governos usam estatística desde o século XIX para melhor compreender as necessidades das populações. A estatística é cada vez mais reconhecida como importante para entender a sociedade, seu progresso e empoderar indivíduos.

2. A Estatística é um ramo da Matemática que dispõe de
processos apropriados para recolher, organizar, classificar,
apresentar e interpretar determinados conjuntos de dados.

3. A Estatística tem por objectivo extrair informação dos dados para
obter uma melhor compreensão das situações que representam.
Na vida de todos os dias, cada vez mais é reconhecida a importância da
estatística. Através do seu estudo e conhecimento é possível compreender
a sociedade e o seu progresso e também potencializar a capacidade de
cada indivíduo ser mais interveniente nesse próprio progresso.
A Importância da Estatística
No intuito de conhecerem melhor a população e as suas necessidades, os
governos de quase todos os países, a partir do século XIX, recorrem à
estatística.

4. Variáveis estatísticas
 Na figura ao lado observamos
um conjunto de pessoas. Cada
pessoa tem muitas
características ou variáveis.
• a cor do cabelo;
• a altura;
• o sexo;
• …

5. Variáveis estatísticas.
Variáveis quantitativas e variáveis qualitativas
Num estudo estatístico parte-se de um conjunto. Cada elemento desse
conjunto (a unidade estatística) tem, provavelmente, muitos
caracteres, características ou atributos
a que chamamos variáveis.
Por exemplo:
Variáveis Valor observado
Peso de uma pessoa 65 kg
Marca de um automóvel Opel
Velocidade do carro 80 km/h
Cor dos olhos Azul
Tipos de dados
Ao resultado de uma observação
da variável chamamos dado
estatístico
ou simplesmente dado.
Os dados classificam-se em
qualitativos ou quantitativos.

6. Os dados qualitativos representam a informação que indica alguma
qualidade, categoria ou característica não suscetível de medida, mas de
classificação, assumindo várias modalidades.
Os dados quantitativos representam a informação resultante de
características suscetíveis de serem medidas, apresentando-se com
diferentes intensidades, que podem ser de natureza discreta – dados
discretos – ou contínua – dados contínuos.

7. A cor dos olhos, sexo, o desporto favorito, a comida favorita, … são
variáveis qualitativas, porque não se podem medir.
Variáveis Estatísticas
A altura, o número de alunos, o peso, o número de irmãos, … são variáveis
quantitativas, porque se podem medir.
A altura e o peso são variáveis contínuas (podem tomar valores não
inteiros), enquanto o número de alunos e de irmãos são variáveis
discretas (só podem tomar valores inteiros).
Variável estatística: propriedade ou característica que é observada nos
elementos de uma população.

8. Qualitativas
(qualidades)
Quantitativas
(quantidades)
Contínuas Discretas
Variáveis Estatísticas

9. Variáveis qualitativas: ____________________________
Variáveis quantitativas
Contínuas: ______________________
Discretas: _______________________
Exercício 3
Num estudo feito numa escola, recolheram-se dados referentes às
seguintes variáveis:
(A) idade (D) número de irmãos (G) local de estudo
(B) ano de escolaridade (E) desporto preferido (H) tempo gasto diariamente no estudo
(C) sexo (F) distância de casa à escola (I) nota na disciplina de Matemática
A, B, D, I
C, E, G
F, H

10. Organização e Tratamento de dados
Relativamente a uma amostra de 20
portugueses, com mais de 18 anos,
obtiveram-se os seguintes dados relativos
ao seu estado civil.
Solteiro Solteiro Casado Solteiro Solteiro
Divorciado Solteiro Viúvo Casado Divorciado
Solteiro Casado Solteiro Solteiro Casado
Casado Solteiro Solteiro Casado Divorciado

11. Tabela de Frequências
Estado Civil
Frequência
Absoluta
Frequência Relativa
Decimal Percentagem (%)
Solteiro
Casado
Viúvo
Divorciado
Total
10
20
0,5=
6
20
0,3=
1
20
0,05=
3
20
0,15=
1000,5 50%× =
1000,3 30%× =
100,05 50 %× =
1000,15 15%× =
10
6
1
3
20 1 100%
Frequência absoluta de um
acontecimento é o número de vezes
que esse acontecimento se repete.
Frequência relativa de um acontecimento é
o quociente entre a frequência absoluta e o
número total de elementos.

12. N.º de filhos por casal Frequência absoluta
Frequência relativa
Decimal Percentagem (%)
TOTAL
Fez-se um inquérito a 15 casais sobre o número de filhos que
tinham. As respostas foram as seguintes.
Exercício 4
a) Organiza os dados numa tabela de frequências absolutas e relativas.

13. b) Quantos casais não têm filhos?
N.º de filhos por casal Frequência absoluta
Frequência relativa
Decimal Percentagem (%)
0 3 0,2 20%
1 5 0,33 33%
2 4 0,27 27%
3 2 0,13 13%
4 1 0,07 7%
TOTAL 15 1 100%
3 casais

14. Medidas de Localização
Moda, Média e Mediana

15. Moda
A moda de um conjunto de dados é o elemento mais frequente (ou
seja, que se repete um maior número de vezes).
A moda representa-se por Mo.
Exemplo:
Uma caixa dez pregos com os seguintes comprimentos:
15; 10; 10; 5; 5; 10; 15; 15; 10; 10
Moda = Mo = 10, porque é o valor mais frequente.

16. Média Aritmética
11 13 15 17
Média X 14
4
+ + +
= = =
Exemplo:
Um casal tem quatro filhos com as idades: 11, 13, 15 e 17 anos.
A média (ou média aritmética) de um conjunto de valores é o quociente
entre a soma de todos os valores e o número total de elementos.
A média representa-se por .X

17. A mediana é o valor que ocupa a posição central da variável estatística.
A mediana representa-se por .°X
Se o número de dados é ímpar, a mediana é o valor do dado que ocupa a
posição central.
Mediana
Para se determinar a mediana deve-se começar por escrever os valores da
variável por ordem crescente (ou decrescente).

18. Se o número de dados é ímpar, a mediana é o valor do dado que ocupa a
posição central.
Exemplo:
Mediram-se as alturas de 7 soldadinhos de chumbo e obtiveram-se os
resultados que depois de ordenados são:
Como o número total de
dados é ímpar, há um
valor central: 168.
~

19. Como o número total de dados
é par, há dois valores centrais:
168 e 170.
Mediram-se as alturas de 6 soldadinhos de chumbo e obtiveram-se os
resultados que depois de ordenados são:
Exemplo:
Se o número de dados é par, a mediana é a média aritmética dos dois
valores centrais.
~

20. 0
1
2
3
4
4
10
7
3
1
Número de
filhos
Frequência
absoluta
A família do Sr. Alberto tem 25 casais. A tabela e o gráfico seguintes
foram construídos com base no número de filhos do casais que
constituem a família Sr. Alberto.
Exemplo:
Vamos determinar a média, a moda e a mediana quando os dados
têm que ser lidos numa tabela ou num gráfico.

21. 0
1
2
3
4
4
10
7
3
1
Número
de filhos
Frequência
absoluta
 Moda = _____
Média = = =
n.º total de filhos
X
n.º de casais
1

0 4 1 10 2 7 3 3 4
1,48
1 37
25 25
× + × + × + × + ×
= =
O número de observações é ___________. Então a mediana ocupa o lugar número _____.
10 74
0, 0, 0, 0, 1, 1, …, 1, 1, 2, 2, …, 2, 2, 3, 3, 3, 4
ímpar
 Mediana = _____1
13
posição 13

22. Exercício 4:
b) Quantos casais não têm filhos? 3 casais
c) Qual é o número de filhos mais frequente? 1 filho
d) Qual é o número médio de filhos por casal?
e) Qual é a percentagem de casais que têm pelo menos dois filhos?
27 + 13 + 7 = 47 %
0 3 1 5 2 4 3 2 4 1 23
1,5
15 15
;Média
× + × + × + × + ×
= =

23. Tipos de Gráficos

24. Gráfico de Barras
O gráfico de barras foi construído com
as frequências absolutas.
 O gráfico deve ter um título.
 Num dos eixos coloca-se a variável
estatística.
 No outro eixo colocam-se as
frequências absolutas ou relativas.
 As barras são rectângulos todos com
a mesma largura.
 A distância ente as barras deve ser a
mesma.
A altura de cada barra corresponde à
sua frequência.
 No gráfico de barras, a moda é o
elemento que apresenta a maior barra.

25. Gráfico de barras usando as frequências relativas em percentagem.

26. Observe o gráfico.
Análise, representação e redução de dados
Qual é o título
do gráfico?
O título responde
às questões: O quê;
Quando; Onde?
O gráfico tem linhas auxiliares?
Qual é o papel das linhas
auxiliares na elaboração
de um gráfico?
Fica completamente esclarecido
com o gráfico apresentado?
Justifique a resposta.

27. Gráfico de barras
Os gráficos de barras são
fáceis de construir e de ler,
por isso são os mais
populares. Apresento quatro
tipos de gráficos de barras.

28. Gráfico de Linhas
 O gráfico deve ter um título.
 Num dos eixos coloca-se a variável
estatística.
 No outro eixo colocam-se as
frequências absolutas ou relativas.
 O gráfico de linhas é um conjunto
de pontos conectado por uma única
linha.
 Cada ponto corresponde à sua
frequência.

29. Gráfico Circular
A frequência relativa de “Solteiros” é de 0,5.
0,5 360º 180º× =
Vamos determinar a amplitude do sector relativo aos portugueses com o
estado civil “Solteiro”.

30. Procedemos da seguinte forma:
I – Desenhávamos uma circunferência:
II – Marcávamos um raio:
III – A partir desse raio, marcávamos, com o
transferidor , o ângulo de 180º:
IV – Escrever a percentagem respectiva:
Para representarmos 50% num gráfico circular, temos que marcar um
ângulo de 180º.

31. Para determinarmos a amplitude dos ângulos dos
restantes Estados Civis efectuamos da mesma forma.
Ângulo = frequência relativa × 360º
Nota: O total das amplitudes dos ângulos tem de ser 360º. Se assim
não acontecer, deve-se proceder aos ajustamentos adequados nos
valores dos ângulos.

32.  O gráfico deve ter um título.
 Um gráfico circular ou sectograma
é representado através de um círculo
dividido em sectores.
 A amplitude de cada sector é
proporcional à frequência que
representa.
 A legenda pode estar ao lado ou
incluída no gráfico
Gráfico Circular

33. Os gráficos circulares
são uma boa forma de
mostrar como um todo
está repartido.
Gráficos circulares
Na construção de um gráfico
circular deve-se ter em conta que:
• a amplitude de cada sector é
proporcional à frequência
que representa;
• a legenda pode ser dispensada,
inscrevendo-se os valores
da variável e as suas
frequências nos respectivos
sectores circulares;
• podem-se usar cores diferentes
para os diferentes sectores;
• o gráfico deve ter um título
adequado.
Não é aconselhável construir
um gráfico circular:
• para variáveis que tenham mais
de cinco ou seis modalidades;
• para situações em
que os sectores resultam
aproximadamente com
a mesma amplitude;
• para sectores com amplitudes
muito pequenas.
Não é formalmente correcto
apresentar gráficos com forma
de elipse ou com sectores
separados.

34. Muito antes de o homem primitivo inventar a escrita, conseguiu através
de desenhos e símbolos deixar informações importantes.
Também nos nossos dias os desenhos e os símbolos são úteis para
comunicar informações importantes que podem ser compreendidas por
diferentes pessoas, mesmo que não falem a mesma língua.
Exemplos disso são os pictogramas que se utilizam muito em estatística.
Pictograma
Um pictograma é um gráfico em que os valores são
apresentados por figuras, normalmente relacionadas com o tema
em estudo.

35. Indique um valor aproximado para
o número de pessoas que
participaram no inquérito.
Pictogramas
O pictograma seguinte refere-se à opinião recolhida, através
de um inquérito, de um grupo de pessoas
que acabou de assistir a um filme.

36. Os pictogramas são gráficos muito semelhantes aos
gráficos de barras.
A principal diferença reside no facto de se utilizarem símbolos alusivos
à situação concreta em estudo por forma a tornarem-se mais atraentes.
Na construção de um pictograma devem ter-se em atenção os
seguintes aspectos:
• Indicar no gráfico o significado de cada figura ou símbolo utilizados.
• Utilizar símbolos ou figuras sugestivos em relação à variável
estatística em estudo.
• Utilizar sempre o mesmo símbolo ou símbolos.
• Desenhar os símbolos em linhas ou colunas.
• Espaçar igualmente os símbolos.
• Expressar as diferentes frequências através de um maior ou menor
número de símbolos, não aumentando ou diminuindo o tamanho
do símbolo.
• O gráfico deve ter um título adequado.

37. Para efectuarmos um estudo sobre a altura dos alunos do 3.º ciclo da
escola, escolheu-se uma amostra constituída por 23 alunos.
Os dados obtidos, em centímetros, foram os seguintes:
145 151 147 167 175 174 153 167 173 162 169 171
158 149 170 167 168 175 174 157 149 150 156
Como deveremos organizar este tipo de dados?
Agrupamento em classes

38. Tabela de frequências
Classes
(Altura dos alunos) N.º de alunos
[145,151[ 5
[151,157[ 3
[157,163[ 3
[163,169[ 4
[169,175[ 8
Total 23
Para organizar estes dados vamos agrupá-los em classes. Tendo em conta o
menor e o maior valor da tabela e que cada classe tem que ter a mesma
amplitude, ou seja, a diferença entre o extremo superior e o extremo
inferior da classe.
Na 1.ª classe estão incluídas as
alturas maiores ou iguais a 145
e menores do que 151.
.
145 151 147 167 175 174 153 167 173 162 169 171
158 149 170 167 168 175 174 157 149 150 156

39. Os gráficos das distribuições usando dados contínuos têm um aspecto diferente
dos gráficos de barras das distribuições de dados discretos. Neste caso
chamam-se histogramas.
Histograma é um gráfico de barras formado por um conjunto de rectângulos
adjacentes (colados), tendo cada um deles por base um intervalo de classe e por
altura a respectiva frequência.
Histograma

40. Polígono de frequências
Se num histograma unires por segmentos de recta os pontos médios dos lados
superiores de cada rectângulo do histograma, como se fez em baixo, obténs
uma outra forma de apresentar a distribuição, que se chama polígono de
frequências.
Nota: Para obtermos os pontos nos extremos da linha poligonal, devemos imaginar
que existe uma classe com a mesma amplitude das restantes e frequência zero,
determinar o ponto médio desta classe e uni-lo aos restantes.

41. Nota: A média e a mediana apenas podem ser determinadas em dados
quantitativos, a moda pode ser determinada em dados quantitativos e
qualitativos.
Quando os dados estão agrupados por classes temos que:
 A classe modal corresponde à classe com maior frequência.
 A média de um conjunto de dados agrupados corresponde à média das
marcas das classes (valor médio de cada classe), tendo em conta as
frequências respectivas.
 A classe mediana corresponde à classe que incluiu o valor central.

42. Diagrama de Caule-e-folhas
Os resultados de 16 testes, numa escala de 0 a 100,
foram os seguintes:
35, 78, 50, 63, 86, 73, 57, 82,
59, 75, 66, 79, 83, 71, 94, 59

43. 3 5
5 0 7 9 9
6 3 6
7 1 3 5 8 9
8 2 3 6
9 4
Esta representação chama-se diagrama de caule-e-folhas.
O caule é a coluna com os números 3, 5, 6, 7, 8 e 9 que representam o
algarismo das dezenas e as folhas que representam o algarismo das
unidades de cada um dos dados.
Pode-se organizar este conjunto de dados utilizando uma representação
gráfica do tipo seguinte:
35, 78, 50, 63, 86, 73, 57, 82,
59, 75, 66, 79, 83, 71, 94, 59

44. 35, 78, 50, 63, 86, 73, 57, 82,
59, 75, 66, 79, 83, 71, 94, 59
3 5
5 0 7 9 9
6 3 6
7 1 3 5 8 9
8 2 3 6
9 4
35
78, 73, 75, 79, 71
Ordenando os algarismos das unidades vem:1, 3, 5, 8,9
Isto é:

45.  Representa os dados, separando cada
valor em duas partes: o caule (valor à
esquerda do traço vertical) e a folha
(algarismo à direita do traço vertical).
 O valor a colocar no caule são das
dezenas, centenas e milhares. O valor a
colocar na folha são as unidades. Aqui
repetimos as unidades quantas vezes o
número aparece.
 Não é necessário construir previamente
uma tabela de frequências.
Diagrama de Caule-e-folhas

46. Diagrama de Extremos e Quartis
O Diagrama de extremos e quartis é uma representação
gráfica onde se realçam algumas características da
amostra.
Para tal, começa-se por determinar as seguintes
medidas da amostra: os extremos (o mínimo e o
máximo), a mediana e o 1.º e 3.º quartis.

47. Classificações dos testes de Matemática

48. Vamos determinar o mínimo e o máximo, a mediana e o 1.º
e 3.º quartis das classificações do António.
65, 70, 75, 75, 80, 85
Mínimo: 65 Máximo: 85
~

49. A mediana divide a distribuição em duas partes iguais.
António:

50. Os quartis são valores da variável que dividem a
distribuição em 4 partes iguais, cada uma delas
com 25% dos dados totais ordenados.
1.º Quartil 3.º Quartil2.º Quartil

51. A mediana divide o conjunto de dados em duas
partes com igual percentagem de elementos, 50%.
Assim, para determinar os quartis, basta calcular a
mediana de cada uma dessas duas partes, obtendo,
desta forma, quatro partes com igual percentagem.

52. 65, 70, 75, 75, 80, 85
65, 70, 75 75, 80, 85
Vamos determinar os quartis para as classificações do
António
80= =33.ºQuartil Q7011.ºQuartil Q= =

53. O primeiro quartil, Q1, separa os primeiro 25% dos dados
ordenados dos restantes 75%.
O segundo quartil, Q2, corresponde ao valor da mediana.
O terceiro quartil, Q3, separa os primeiro 75% dos dados iniciais
dos últimos 25%.

54. Para construir o diagrama de extremos e quartis referente às classificações
do António, basta proceder do seguinte modo:
1.Traçar uma recta orientada na horizontal (ou vertical) que inclua o
mínimo e o máximo do conjunto de dados.
2.A par da recta orientada, desenhar um rectângulo entre o 1.º e o 3.º
quartil e colocar um traço para assinalar a mediana.
3.Marcar dois segmentos de recta verticais ao lado do rectângulo
correspondentes ao mínimo e máximo.
4.Unir os pontos médios dos segmentos de recta do mínimo e do 1.º quartil
e os pontos médios dos segmentos de recta do máximo e do 3.º quartil.
Mín: 65
Máx: 85
Med.: 75
Q1: 70
Q3:80

55. Diagrama de Extremos e Quartis
O Diagrama de Extremos e Quartis pode ser colocado na
horizontal ou vertical. Este diagrama também é conhecido por
diagrama de caixa e bigodes.

56. Vamos construir o diagrama de extremos e quartis das
classificações da Bárbara.

57. 73, 74, 75, 75, 76, 77
Mínimo: 73 Máximo: 77
Exercício da ficha de trabalho:
Vamos ordenar as classificações da Bárbara.
~

58. 73, 74, 75, 75, 76, 77
73, 74, 75 75, 76, 77
Vamos determinar os quartis para as classificações da Bárbara.
76= =33.ºQuartil Q74= =11.ºQuartil Q

59. Diagrama de extremos e quartis das classificações da Bárbara.
Mín: 73
Máx: 77
Med.: 75
Q1: 74
Q3: 76

60. A amplitude e a amplitude interquartis são medidas
indicadas para estudar a dispersão dos dados.
A amplitude é a diferença entre o máximo e o mínimo do
conjunto de dados (os extremos).
Amplitude e Amplitude Interquartis
A = máximo − mínimo
A amplitude é muito dependente dos valores extremos do
conjunto de dados, pelo que, em determinadas situações, pode
não descrever correctamente a sua dispersão.

62. A amplitude interquartis é a diferença entre o 3.º quartil e o
1.º quartil.
AIQ = Q3 − Q1
A amplitude interquartis fornece informação acerca da amplitude
do intervalo que contém 50% dos dados centrais.
Como é óbvio, quanto mais variados forem os dados, maior será a
amplitude interquartis.

64. Média
Medidas de
localização central
Medidas de
localização
Medidas de
dispersão
Mediana
Moda
Quartis
Amplitude
Amplitude
interquartis