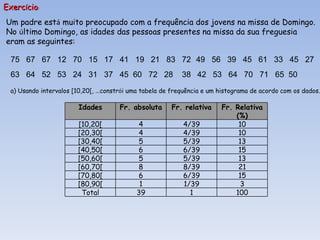
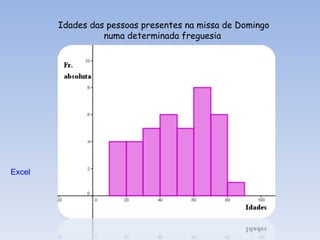
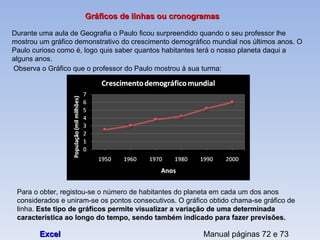
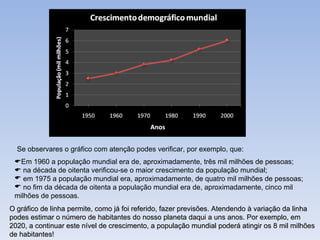
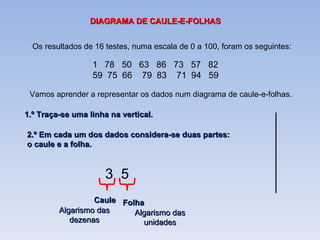
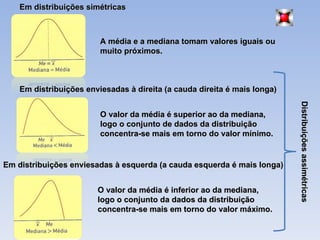
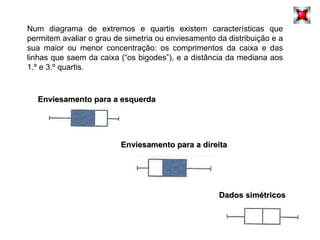
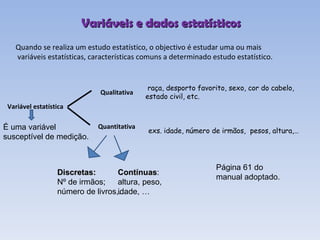
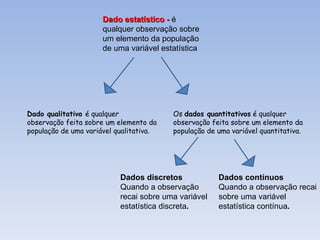
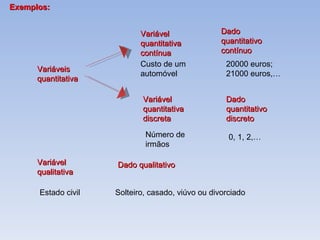
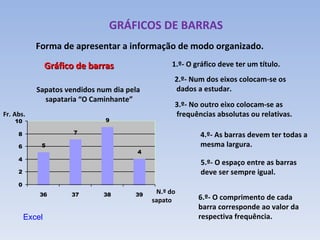
O documento introduz os conceitos básicos de estatística, incluindo a definição de população e amostra, variáveis qualitativas e quantitativas, recolha e organização de dados em tabelas e gráficos. Explica como a estatística é usada para analisar conjuntos de dados e tirar conclusões sobre as características das fontes de onde os dados foram retirados.

1. ESTATÍSTICA

3. Introdução ao estudo da Estatística Ao folheares os jornais ou revistas, ao consultares um livro de História, Ciências ou outra disciplina já encontraste informação sobre os mais diversos assuntos, apresentada sob a forma de tabelas e gráficos .

6. Recolher e organizar a informação é muito importante no mundo actual. Analisando os dados recolhidos podem tirar-se conclusões que permitem prever situações e planificar actividades com muita segurança. Cabe à Estatística, recolher, organizar e analisar a informação, tirar conclusões e fazer previsões. A Estatística é um dos ramos da Matemática que se dedica à recolha, análise e interpretação de dados. Preocupa-se com os métodos de recolha, organização, resumo, apresentação e interpretação dos dados, assim como em tirar conclusões sobre as características das fontes donde estes foram retirados, para melhor compreender as situações.

7. A Estatística parte da observação de conjuntos de pessoas, objectos ou acontecimentos. Exemplo 1- Idade dos alunos de uma turma Quando se pretende saber a idade dos alunos de uma turma é possível fazê-lo, perguntando a cada um a sua idade, dado que o número de inquiridos é finito e pouco numeroso. Neste caso, podemos dizer que a população - são todos os alunos da turma. Ao conjunto de pessoas, objectos ou acontecimentos que têm uma ou mais características em comum e que vai ser alvo de um estudo estatístico chamamos POPULAÇÃO OU UNIVERSO ESTATÍSTICO. Censos e sondagens. População e amostra

9. Nem sempre é possível estudar toda a população. Por vezes, temos de escolher uma amostra , ou seja, uma parte representativa da população. Exemplo II- Sondagem Quando se faz uma sondagem, não se interroga toda a população, mas apenas uma parte desta, ou seja uma amostra. Intenção de voto para as eleições de 1996 Neste caso, População - conjunto de todos os eleitores Amostra- 1013 indivíduos dos 18 aos 64 anos residentes em Lisboa e no Porto, em lares com telefone. AMOSTRA – é um subconjunto da população que se estuda com o objectivo de tirar conclusões sobre a população onde foi recolhida. DIMENSÃO DA AMOSTRA- é o nº de elementos da amostra.

10. Curiosidade – O primeiro censo geral da população portuguesa teve lugar em 1864. São feitos de 10 em 10 anos e trata-se de uma contagem oficial dos indivíduos que vivem em Portugal. Quando o estudo estatístico tem em conta toda a população, estamos perante um censo ou recenseamento ; quando incide sobre uma amostra da população, trata-se de uma sondagem. Escola virtual Estudo científico efectuado a partir da análise de uma amostra. Definições - pág. 58 do manual.

12. Variáveis e dados estatísticos Quando se realiza um estudo estatístico, o objectivo é estudar uma ou mais variáveis estatísticas, características comuns a determinado estudo estatístico. Variável estatística Qualitativa Quantitativa raça, desporto favorito, sexo, cor do cabelo, estado civil, etc. exs. idade, número de irmãos, pesos, altura,… É uma variável susceptível de medição. Discretas: Nº de irmãos; número de livros,… Contínuas : altura, peso, idade, … Página 61 do manual adoptado.

13. Dado qualitativo é qualquer observação feita sobre um elemento da população de uma variável qualitativa. Os dados quantitativos é qualquer observação feita sobre um elemento da população de uma variável quantitativa. Dado estatístico - é qualquer observação sobre um elemento da população de uma variável estatística Dados discretos Quando a observação recai sobre uma variável estatística discreta . Dados contínuos Quando a observação recai sobre uma variável estatística contínua .

14. Exemplos: Custo de um automóvel Variável quantitativa contínua Dado quantitativo contínuo 20000 euros; 21000 euros,… Variável quantitativa discreta Dado quantitativo discreto Número de irmãos 0, 1, 2,… Variável qualitativa Estado civil Solteiro, casado, viúvo ou divorciado Dado qualitativo Variáveis quantitativa

15. Exercícios do manual adoptado das páginas 59 e 61.

16. RECOLHA, ORGANIZAÇÃO E APRESENTAÇÃO DE DADOS

17. RECOLHA, ORGANIZAÇÃO E APRESENTAÇÃO DE DADOS Tabela de frequências absoluta e relativa – forma de apresentar os dados estatísticos de modo organizado. Exemplo: Duas sapatarias, “O Caminhante” e o “O Confortável”, efectuaram um estudo para saber qual o número de sapatos femininos mais procurados. Para tal, consideraram como amostra todos os pares de sapatos vendidos num certo dia, registando o seu número. O Caminhante 36 38 36 37 37 39 38 38 36 39 37 37 38 38 38 39 37 36 36 37 38 38 37 38 39 O Confortável 38 38 37 39 36 38 37 36 37 37 37 38 38 37 38 38 37 36 38 37 38 37 37 36 37 Vamos construir a tabela de frequência destas duas distribuições.

18. a) Qual é o número mais pedido em cada sapataria? Caminhante - 38 Confortável – 37 b ) Em qual das duas sapatarias houve uma maior percentagem de pedidos do número 37? Na sapataria “O Confortável”, 44%. A frequência relativa de um acontecimento é o quociente entre a frequência absoluta e o número total de dados . Definições: A frequência absoluta ou efectivo de um dado estatístico é o número de vezes que esse acontecimento (dado) se verifica. Agora, dá-mos facilmente resposta a qualquer questão.

19. GRÁFICOS

20. São muito utilizados para representar graficamente dados qualitativos ou quantitativos discretos. GRÁFICOS DE BARRAS

21. Sapatos vendidos num dia pela sapataria “O Caminhante” Forma de apresentar a informação de modo organizado. Gráfico de barras 6.º- O comprimento de cada barra corresponde ao valor da respectiva frequência. 1.º- O gráfico deve ter um título. 2.º- Num dos eixos colocam-se os dados a estudar. 3.º- No outro eixo colocam-se as frequências absolutas ou relativas. 4.º- As barras devem ter todas a mesma largura. 5.º- O espaço entre as barras deve ser sempre igual. Excel GRÁFICOS DE BARRAS N.º do sapato Fr. Abs.

22. Exercícios do manual adoptado da página 67.

23. GRÁFICOS CIRCULARES

24. GRÁFICOS CIRCULARES Os gráficos circulares são muito utilizados. São constituídos por círculos divididos em sectores em que as amplitudes dos sectores são proporcionais às respectivas frequências. Podem mostrar-nos as frequências absolutas, mas, na maioria das vezes, apresentam as frequências relativas sob a forma de percentagem.

25. Exemplo 1 Durante um campeonato, o número de vitórias, de empates e de derrotas de uma equipa desportiva tem a seguinte distribuição: A partir da informa ç ão dada pode-se construir uma tabela de frequências . Para construir um gr á fico circular come ç a-se por determinar as amplitudes dos ângulos correspondentes aos sectores circulares. Vitórias 10 Empates 7 Derrotas 8 Resultados Freq. absoluta Freq. relativa Freq. Relativa (em %) Vitórias 10 0,4 40 Empates 7 0,28 28 Derrotas 8 0,32 32 Total 25 1 100

26. Sector correspondente à s vit ó rias Considerando que um c í rculo representa o n ú mero total dos dados (100%) e que corresponde 360º, utilizando uma regra de 3 simples, tem-se: 100% ______360 º 40% ______ x Assim, podemos concluir que, para determinar a amplitude de um sector circular, basta, multiplicar a frequência relativa por 360º. Conhecidas as amplitudes dos diversos sectores, com uma r é gua, um transferidor e um compasso faz-se a constru ç ão do diagrama circular, percorrendo as seguintes fases: Amplitude = frequência relativa  360º Resultados Freq. absoluta Freq. relativa Freq. Relativa (em %) Vitórias 10 0,4 40 Empates 7 0,28 28 Derrotas 8 0,32 32 Total 25 1 100 Amplitude fix360º 144º 100,8º 115,2º 360º

27. Desenha-se um c í rculo e marca-se um raio qualquer. A partir desse raio, com o transferidor, marca-se um arco de 144º de amplitude. Tendo o primeiro sector marcado, os restantes são obtidos, como é sugerido nas figuras abaixo.

28. Assim, os resultados podem ser representados no seguinte diagrama circular . Por fim, atribuí-se um t í tulo e uma legenda ao gráfico circular. Nunca te esqueças que os gráficos transmitem informação. Por isso, é fundamental atribuir um título ao gráfico e legendá-lo.

29. Exerc í cio: Regressemos ao exemplo da sapataria “ O Confort á vel ” . Número de sapatos femininos vendidos num dia pela sapataria “O Confortável” Excel Número Freq. absoluta Freq. relativa 36 4 0,16 37 11 0,44 38 9 0,36 39 1 0,04 Total 25 1 Amplitudes fix360º 0,16x360º = 58º 158º 130º 14º 360

30. PICTOGRAMAS Um pictograma é um gráfico que utiliza figuras ou símbolos para apresentar a informação.

31. Para construir um pictograma: Começa-se por escolher um símbolo alusivo ao tema em estudo e atribui-se-lhe um certo valor; representa-se graficamente a informação repetindo esse símbolo em linhas ou colunas igualmente espaçadas; indica-se o significado de cada símbolo; dá-se um título ao gráfico.

32. DADOS AGRUPADOS EM CLASSES

33. Exemplo Os pesos, em quilogramas, dos 36 alunos de uma escola de t é nis são os seguintes: 55 66 60 53 58 50 58 69 57 59 59 64 56 59 55 59 64 58 54 57 61 51 55 70 65 58 60 61 62 56 54 61 60 62 58 61 1. Elabora uma tabela de frequências. 2. Quantos alunos pesam: 2.1) menos de 58 kg? 2.2) pelo menos 62kg? 2.3) menos de 66 kg mas 62 kg ou mais? Como os dados são muitos e variados, é dif í cil responder a estas questões. Nestes casos é conveniente agrupar os dados em classes. Isto é :

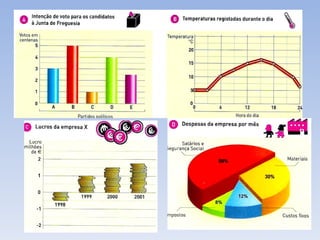
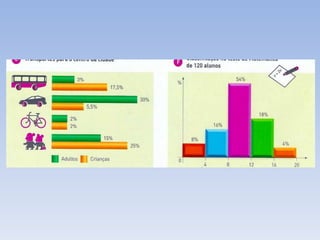
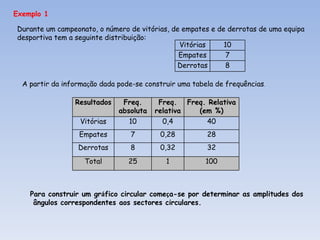
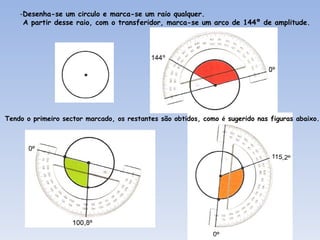
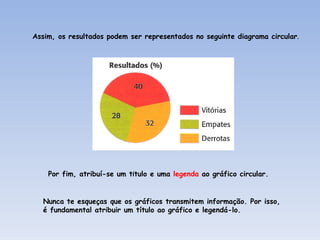
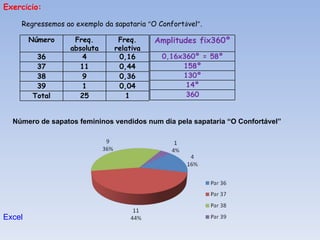
34. Como construímos as classes? Identificámos os valores máximos e mínimo observados. Máximo 70 kg Mínimo 50 kg Adoptámos 5 classes de amplitude 4 (p.e.) Construímos uma tabela de frequências . 55 66 60 53 58 50 58 69 57 59 59 64 56 59 55 59 64 58 54 57 61 51 55 70 65 58 60 61 62 56 54 61 60 62 58 61 2.1) 12 alunos. 2.2) 8 alunos. 2.3) 5 alunos . 2. Quantos alunos pesam: 2.1) menos de 58 kg? 2.2) pelo menos 62kg? 2.3) menos de 66 kg mas 62 kg ou mais? Agora, dá-mos facilmente resposta a qualquer questão. Classes Frequência absoluta [50,54[ 3 [54,58[ 9 [58,62[ 16 [62,66[ 5 [66,70] 3 Total 36

35. HISTOGRAMA O histograma usa-se para representar graficamente dados agrupados em classes. É constitu í do por uma sucessão de rectângulos adjacentes, tendo por base o intervalo da classe e a á rea das suas barras é proporcional à frequência da classe que representa. Na constru ç ão de um histograma deve ter-se em aten ç ão o seguinte: O gr á fico deve ter um t í tulo; Os dados devem ser agrupados em classes; No eixo horizontal representam-se os intervalos das classes; No eixo vertical representam-se as frequências absolutas ou relativas das classes; As barras são desenhadas verticalmente e sem qualquer espa ç o entre elas; A área de cada barra é directamente proporcional à respectiva frequência. Vamos então construir o histograma, respeitante à distribuição anterior.

36. Exerc í cio : Um padre est á muito preocupado com a frequência dos jovens na missa de Domingo. No ú ltimo Domingo, as idades das pessoas presentes na missa da sua freguesia eram as seguintes: 75 67 67 12 70 15 17 41 19 21 83 72 49 56 39 45 61 33 45 27 63 64 52 53 24 31 37 45 60 72 28 38 42 53 64 70 71 65 50 a) Usando intervalos [10,20[, … constr ó i uma tabela de frequência e um histograma de acordo com os dados. Idades Fr. absoluta Fr. relativa Fr. Relativa (%) [10,20[ 4 4/39 10 [20,30[ 4 4/39 10 [30,40[ 5 5/39 13 [40,50[ 6 6/39 15 [50,60[ 5 5/39 13 [60,70[ 8 8/39 21 [70,80[ 6 6/39 15 [80,90[ 1 1/39 3 Total 39 1 100

37. Idades das pessoas presentes na missa de Domingo numa determinada freguesia Excel

38. b) Comenta a preocupa ç ão do padre? c) Quantas pessoas têm 50 anos ou mais? d) Qual a percentagem de pessoas que têm pelo menos 30 anos? Idades Fr. absoluta Fr. relativa Fr. Relativa (%) [10,20[ 4 4/39 10 [20,30[ 4 4/39 10 [30,40[ 5 5/39 13 [40,50[ 6 6/39 15 [50,60[ 5 5/39 13 [60,70[ 8 8/39 21 [70,80[ 6 6/39 15 [80,90[ 1 1/39 3 Total 39 1 100

39. GRÁFICOS DE LINHAS OU CRONOGRAMAS

40. Gráficos de linhas ou cronogramas Manual páginas 72 e 73 Durante uma aula de Geografia o Paulo ficou surpreendido quando o seu professor lhe mostrou um gráfico demonstrativo do crescimento demográfico mundial nos últimos anos. O Paulo curioso como é, logo quis saber quantos habitantes terá o nosso planeta daqui a alguns anos. Observa o Gráfico que o professor do Paulo mostrou à sua turma: Para o obter, registou-se o número de habitantes do planeta em cada um dos anos considerados e uniram-se os pontos consecutivos. O gráfico obtido chama-se gráfico de linha. Este tipo de gráficos permite visualizar a variação de uma determinada característica ao longo do tempo, sendo também indicado para fazer previsões. Excel

41. Se observares o gráfico com atenção podes verificar, por exemplo, que:  Em 1960 a população mundial era de, aproximadamente, três mil milhões de pessoas;  na década de oitenta verificou-se o maior crescimento da população mundial; em 1975 a população mundial era, aproximadamente, de quatro mil milhões de pessoas; no fim da década de oitenta a população mundial era de, aproximadamente, cinco mil milhões de pessoas. O gráfico de linha permite, como já foi referido, fazer previsões. Atendendo à variação da linha podes estimar o número de habitantes do nosso planeta daqui a uns anos. Por exemplo, em 2020, a continuar este nível de crescimento, a população mundial poderá atingir os 8 mil milhões de habitantes!

42. DIAGRAMA DE CAULE-E-FOLHAS Os resultados de 16 testes, numa escala de 0 a 100, foram os seguintes: 78 50 63 86 73 57 82 59 75 66 79 83 71 94 59 Vamos aprender a representar os dados num diagrama de caule-e-folhas. 1.º Traça-se uma linha na vertical. 2.º Em cada um dos dados considera-se duas partes: o caule e a folha. 3 5 Caule Folha Algarismo das dezenas Algarismo das unidades

43. 3 5 6 9 8 7 3.º Do lado esquerdo da linha vertical colocam-se os caules sem os repetir. 78 50 63 86 73 57 82 59 75 66 79 83 71 94 59 4.º Do lado direito da linha vertical colocam-se as folhas correspondentes aos respectivos caules. 5 0 3 4 6 8 9 7 6 2 3 9 3 1 5 9 5. Para cada caule ordenam-se as folhas, por ordem crescente. 3 5 6 9 8 7 5 0 3 4 2 1 9 7 6 3 3 9 6 9 5 8 Vantagens: Não se perde informação; È de fácil construção; Por simples observação, permite verificar facilmente o modo como os dados estão distribuídos; Possibilita a ordenaçã o dos dados da amostra;

44. Observação: O caule pode conter um qualquer número de algarismos mas, por norma, cada folha é constituída apenas por um algarismo. Por exemplo: Para representar 230, procede-se do seguinte modo: 23 0

45. Que gráficos se deve utilizar? Nos dados de natureza qualitativa, os gráficos mais utilizados são: Gráficos de barras; Gráficos de pontos; Pictogramas; Diagramas circulares. Nos dados de natureza quantitativa discreta, os gráficos mais utilizados são: Gráficos de barras; Gráficos de pontos. Nos dados de natureza quantitativa contínua, o gráfico mais utilizado é o: Histograma O diagrama caule-e-folhas pode ser usado para dados contínuos ou discretos . Os gráficos de linhas usam-se para analisar a evolução de uma variável com o tempo.

46. MEDIDAS DE LOCALIZAÇÃO OU MEDIDAS DE TENDÊNCIA CENTRAL

47. Habitualmente os valores de um conjunto de dados estão dispersos, pelo que é aconselhável verificar se os valores têm tendência a concentrar-se em torno de um valor central ou médio. As medidas estatísticas que nos dão uma indicação deste valor, designam-se por medidas de localização ou medidas de tendência central . São usadas para indicar um valor que represente melhor um conjunto de dados. Nesta aula vais poder recordar a média aritmética e a moda e aprender uma nova medida estatística: a mediana . No nosso quotidiano colocámos questões tais como: Qual é o programa de televisão com maior audiência? Qual é a altura média dos habitantes de uma cidade? Qual é a classificação mediana dos alunos de uma turma a Matemática? Qual é o tempo médio necessário para produzir um medicamento? Quantos golos sofre em média, uma equipa por jogo?

48. M é dia aritm é tica

49. Exemplo 1 A visita de estudo. Alguns amigos foram a uma visita de estudo. Cada um deles levou uma certa quantia em dinheiro para as suas despesas. Patrícia €15 Catarina €35 Bruno €40 Joana €10 Carlota €50 Sebastião €60 Pedro € 35 João €50 Susana €55 Daniel €35 Vera €55 Se os amigos juntarem o dinheiro, e dividirem igualmente entre si o total do dinheiro, com quanto ficará cada um? Cada um dos amigos ficará com 40 euros.

50. Regressemos ao exemplo da sapataria “O Confortável”. A partir de uma tabela de frequências, também podemos determinar a média. Para calcular a média de um conjunto de valores, ____________ todos os valores e ___________ a soma pelo número de valores considerados. Representa-se por . Nota: Só se pode calcular a média se os dados forem _____________ Qual a média do número do par de sapatos vendidos nesse dia? quantitativos. somam-se divide-se Número Freq. absoluta 36 4 37 11 38 9 39 1 Total 25

51. Moda

52. No ano lectivo 2008/2009, três amigos que frequentam o 10.º ano, tiveram nos testes de Matemática, as seguinte notas: ZÉ: 10 10 12 13 14 16 ARTUR: 10 11 12 13 14 15 RICARDO : 10 10 12 14 14 15 A nota mais frequente é 10. Logo, a moda do conjunto das notas do Z é é 10. ( Unimodal ) Não h á nenhum valor que seja mais frequente. Logo, o conjunto das notas do Artur é amodal , não tem moda. H á dois valores mais frequentes: 10 e 14 Logo, o conjunto das notas do Ricardo é bimodal. Exemplo 2

53. Se os dados estiverem representados, por exemplo, num gráfico de barras, a moda, é o dado (qualitativo ou quantitativo) que corresponde à barra mais alta; se a informação estiver representada num gráfico circular, a moda será o elemento que corresponde ao sector com maior amplitude ou o dado que corresponde ao maior número de símbolos, no caso dos pictogramas. Excel Moda de um conjunto de dados é o valor _______________ de uma distribuição. Representa-se por M 0 . mais frequente

54. Mediana

55.  N ú mero í mpar de dados Exemplo 3 Mediram-se as alturas de 7 soldadinhos de chumbo e obtiveram-se os resultados que, depois de ordenados são: 168 mm é o valor mediano deste conjunto de dados. Mediana é o valor central de uma distribuição. Como o número total de dados é impar há apenas ______________ . Ao valor __________, que neste exemplo é ______ chama-se _________. um valor central central 168 mediana

56.  N ú mero par de dados E se o número de soldadinhos de chumbo fosse 6 ?! A mediana é 169 mm. Repara na altura dos soldadinhos, já ordenada por ordem crescente: Qual será agora a mediana?! Quando o número de valores é par há _______ valores centrais. Logo, a mediana é igual à ________________ dos dois valores centrais. dois média aritmética

57.  Se o número de dados é par, a mediana é igual à _______________ dos dois valores centrais. Representa-se por . Passos que devemos seguir para determinar a mediana.  Verificar se o número de dados é par ou ímpar,  Para determinar a mediana devemos começar por ________ os valores, isto é, escrevê-los por ordem ___________ ou ____________. ordenar crescente decrescente  Se o número de dados é ímpar , a mediana é o valor que ocupa a ______________. posição central média aritmética

58. E se o número de dados for muito grande?! Como fazemos para determinar a mediana? Na tabela seguinte estão representados os valores médios da temperatura do ar, em graus Celsius, durante o mês de Janeiro, numa cidade do interior do país. Identifica a mediana das temperaturas médias do ar. Como o número de dados é ímpar, a mediana só há um valor central. Significa que a mediana será o valor que se encontra em décimo sexto lugar. Então: Temperaturas (ºC) fr. absoluta 4 1 5 1 6 4 7 4 8 4 9 8 10 4 11 4 12 1 Total 31 Fa 1 2 6 10 14 22 26 30 31

59. E se o número de dados for par? Como o número de dados é par, há dois valores centrais. Significa que a mediana será igual à média aritmética dos dois valores centrais. Os valores centrais são os que se encontram em décimo sexto e décimo sétimo lugares . Então: 4 5 6 6 6 6 6 6 7 7 7 7 7 8 8 8 9 9 9 9 9 9 10 10 10 10 11 11 11 11 12 12 15 valores 15 valores Temperaturas (ºC) fr. absoluta 4 1 5 1 6 6 7 5 8 3 9 6 10 4 11 4 12 2 Total 32 Fa 1 2 8 13 16 22 26 30 32

60. Como determinar a média a moda e a mediana, utilizando o Exel. Exemplo: Perguntou-se a um grupo de 19 rapazes de 12 anos o valor da sua mesada (em euros). As respostas foram as seguintes: 0 20 90 20 40 25 10 30 0 50 10 20 25 45 12 60 15 0 60 1. Calcula a média, a moda e a mediana do conjunto de dados. 2. Baseando-te nos cálculos anteriores, um dos elementos desse grupo, o Domingos (que recebia 10 euros mensais), decidiu pedir um aumento da mesada ao seu pai. Qual te parece ter sido a medida de localização utilizada pelo Domingos na sua argumentação? Explica o teu raciocínio. Excel Moda: 0 e 20 bimodal

61. A média é afectada por valores extremos, isto é, por valores muito altos ou muito baixos. Assim, quando o valor da mediana é muito diferente do da média, é aconselhável considerar sempre a mediana como valor de referência mais importante. Portanto, pode-se concluir que:

62. QUARTIS ESCOLA VIRTUAL Já estudamos a média, a moda e a mediana. Agora vamos estudar os quartis. A estas 4 medidas chamamos medidas de localização.

63. Como determinar os quartis? 1.º- Ordenar os dados, por ordem crescente e determinar a mediana. 2.º- O 1.º quartil, Q 1 , é a mediana dos dados que se encontram à esquerda do valor da mediana. 3.º- O 3.º quartil, Q 3 , é a mediana dos dados que ficam para a direita do valor da mediana. A mediana é o 2.º quartil, Q 2.

64. Exemplo: Determinar os quartis num número par de dados 15 16 16 17 18 19 20 21 22 25 Repara que os dados já se encontram ordenados mas, na maioria dos casos não estão, portanto, deves começar por ordená-los. 18,5 1.º Quartil 3.º Quartil A mediana e os quartis são medidas de localização que dividem o conjunto de dados em 4 partes, cada uma delas contendo 25% dos dados. As posições centrais ocupadas por 50% dos dados ficam entre o 1.º e o 3.º quartil.

65. Exemplo: Determinar os quartis num número ímpar de dados 15 16 16 17 18 19 20 21 22 25 26 Como neste caso a mediana pertence ao conjunto de dados, podemos determinar o 1.º e 3.º quartis por dois processos diferentes. 1.º Processo : não considerar o valor da mediana. 15 16 16 17 18 20 21 22 25 26 2.º Processo : considerar o valor da mediana nas duas metades do conjunto de dados. 15 16 16 17 18 19 19 20 21 22 25 26

66. 25% dos dados têm valor igual ou inferior ao 1.º quartil (75% dos dados têm valor superior ou igual ao 1.º quartil); 75% dos dados têm valor igual ou inferior ao 3.º quartil (25% dos dados têm valor superior ou igual a este) 75% 25% 25% 75%

67. AMPLITUDE E AMPLITUDES INTERQUARTIS

68. Consideremos a distribuição das classificações, em percentagem, obtidas pela Helena e pelo Pedro em 5 testes de Matemática. Classificações da Helena Classificações do Pedro 15 25 55 65 70 10 15 55 60 80 Repara que os dois conjuntos de dados têm a mesma média, moda e mediana e no entanto são diferentes. As classificações do Pedro estão mais dispersas . Para resumir os dados, para além das medidas de localização já estudadas, vamos ainda estudar duas medidas de dispersão : a amplitude e a amplitude interquartis.

69. Classificações da Helena Classificações do Pedro 15 25 55 65 70 10 15 55 60 80 70-15=55 80-10=70 amplitude amplitude As classificações do Pedro apresentam uma maior variabilidade entre a classificação mais alta e mais baixa. AMPLITUDE: A amplitude de um conjunto de dados é a diferença entre o maior e o menor desses valores. Amplitude = máximo - mínimo Representa-se por R (range).

70. Classificações da Helena Classificações do Pedro 15 25 55 65 70 10 15 55 60 80 Amplitude interquartis A amplitude interquartis é a diferença entre o 3.º quartil e o 1.º quartil. Amplitude interquartis= Q 3 – Q 1 Fornece-nos informação acerca da amplitude do intervalo que contém 50% dos dados centrais.

71. Propriedades:  A amplitude interquartis será tanto maior quanto mais variabilidade houver entre o conjunto da dados.  Se não houver v ariabilidade, então a amplitude interquartis é zero.  Uma amplitude i nterquartis nula, não significa que não haja variabilidade no conjunto de dados. 1 2 4 4 4 4 4 4 4 4 7 Q 3 Q 1 Q 3 – Q 1 =0

72. DIAGRAMA DE EXTREMOS E QUARTIS Também conhecido por “caixa de bigodes”.

73. Construção: 1.º - Desenhamos um eixo graduado desde o valor do dado mínimo até ao valor do dado máximo. 2.º - Desenhamos um rectângulo cujo comprimento é a diferença entre o 3.º e o 1.º quartis, ou seja, a amplitude interquartis. 3.º - Dividimos o rectângulo por uma linha correspondente à mediana. Completamos o gráfico unido o rectângulo aos extremos. Geogebra Observação: O diagrama de extremos e quartis pode ser construído na vertical ou na horizontal.

74. Exemplo: Para representar as classificações obtidas por duas das suas turmas num determinado teste, o professor de Matemática da Rita construiu os seguintes diagramas: Classificações Em que turma se verificou a classificação mais alta? E a mais baixa? Em que turma se verifica uma maior amplitude das classificações? Indica a percentagem de alunos da turma A que obteve uma classificação positiva no teste. Explica o teu raciocínio. A classificação mais elevada, verificou-se na turma A, 100% e a mais baixa na turma B, 15%. A turma A tem uma amplitude de 60 e a turma B tem uma amplitude de 75. Logo, na turma B verifica-se uma maior amplitude. Para um aluno ter classificação positiva num teste tem de obter, pelo menos, 50%. Na turma A, 50% é o 1.º quartil da distribuição. Como até ao 1.º quartil se encontram 25% dos dados, podemos afirmar que, na turma A, houve 25% de negativas. Assim, 75% dos alunos desta turma tiveram classificação positiva. Turma A Turma B

75. Comparação da posição relativa da mediana e da média. Numa escola há 3 clubes: a Clube do Ambiente, o Clube da Leitura e o Clube da Matemática. Cada clube integra 15 alunos. As distribuições das idades dos alunos dos três cubes são apresentadas a seguir. Determinando a média e a mediana de cada uma das distribuições, obtemos o seguinte:

76. Repara que: No 1.º caso a média e a mediana têm o mesmo valor, então dizemos que a distribuição dos dados é simétrica. No 2.º caso, o valor da média é superior ao da mediana, a distribuição dos dados concentra-se mais junto ao valor mínimo, assim diz-se que distribuição é enviesada à direita. No 3.º caso, o valor da média é inferior ao da mediana, a distribuição dos dados concentra-se mais junto ao valor máximo, assim diz-se que distribuição é enviesada à esquerda.

77. Em distribuições simétricas A média e a mediana tomam valores iguais ou muito próximos. Em distribuições enviesadas à esquerda (a cauda esquerda é mais longa) Em distribuições enviesadas à direita (a cauda direita é mais longa) O valor da média é superior ao da mediana, logo o conjunto de dados da distribuição concentra-se mais em torno do valor mínimo. O valor da média é inferior ao da mediana, logo o conjunto da dados da distribuição concentra-se mais em torno do valor máximo. Distribuições assimétricas

78. Quais as medidas mais adequadas a estudar para cada caso concreto?! Não há regras que nos permitam decidir à priori, qual é a melhor medida a adoptar, uma vez que tal decisão depende inteiramente da situação em estudo. No entanto, há alguns critérios que facilitam a escolha… Se pretendermos saber o valor mais popular num determinado conjunto utiliza-se a moda, por exemplo: “ Qual é a cor automóvel preferida pelos portugueses?” Média, moda, mediana ou amplitude interquartis?

79. E entre a média e a mediana, qual será a melhor opção? Em princípio se todos os valores tiverem a mesma importância, deve-se utilizar a média, por exemplo: “ Em média, quantos golos sofre uma equipa por jogo?” No entanto, a mediana pode ser preferível em alguns casos, já que não é tão afectada por valores muito baixos ou muito altos. Considera, por exemplo, os seguintes dados relativos às notas de um aluno à disciplina de Inglês. Repara que a nota do 1.º teste é muito mais baixa que as restantes . Se o professor entender desvalorizar a 1.ª nota e utilizar todos os dados, qual a medida de tendência central que devia utilizar para melhor traduzir a avaliação do aluno ao longo do ano? 1.º período 2.º período 3.º período 22% 68% 72% 71% 75% 65%

80. Neste caso, o professor deveria escolher a mediana, uma vez que entendeu desvalorizar o resultado do 1.º teste comparativamente aos restantes. 22 65 68 71 72 75 1.º período 2.º período 3.º período 22% 68% 72% 71% 75% 65%

81. Os salários dos 160 operários de uma determinada empresa, distribuem-se de acordo com a seguinte tabela de frequências: Vamos determinar a média e a mediana e analisar os resultados obtidos. O facto de termos obtido uma média de 628 e uma mediana de 475, é reflexo do facto de existirem alguns, embora poucos, salários muito altos, relativamente aos restantes. Repara que, numa perspectiva social, a mediana é uma característica mais importante do que a média. Na realidade 50% dos trabalhadores têm salário inferior a 475 €, embora a média de 628€ (aproximadamente) não transmita essa ideia. Exemplo: Salário (em euros) Frequência absoluta 450 80 500 48 750 20 1500 7 3000 5 Total 160

82. Nestes casos e em muitos outros a média transmite-nos uma falsa informação, assim, o valor da mediana e a amplitude interquartis são os mais adequados para caracterizar a distribuição global dos dados.

83. A média é afectada por valores extremos, isto é, por valores muito altos ou muito baixos. Assim, quando o valor da mediana é muito diferente do da média, é aconselhável considerar sempre a mediana e a amplitude interquartis como valores de referência mais importante. Portanto, pode-se concluir que:

84. Como dizer ao meu pai que tive 8 (0 a 20) a matemática? O teste de Estatística não que correu bem, tive um 8. Como vou dizer ao meu pai? Pensando bem, o resto das notas da turma não foram famosas. Somos 10 e os resultados foram catastróficos! O geniozinho teve 19, é claro, mas, excluindo-o houve um 10, quatro 9 e três 2. Bom, a moda é 9 e a mediana também é 9, mas a média é de 7,9. Boa! Direi ao meu pai que mesmo assim estou acima da média. Mais um 8! Mas, desta vez as notas são: 2, 3, 4, 5, 7, 8 (eu), 9, 9, 18 e 19 (o génio). A média é 8,4; bolas, estou abaixo dela. A moda é 9. Já sei, direi ao meu pai que estou acima da mediana (7,5). Não tenho mesmo sorte nenhuma! Não saio do 8! Deve ser culpa da prof! Desta vez as questões eram tão difíceis que houve três 7. Os outros tiveram 19 (sempre o mesmo), 18, 12, 11, 10 e 2 (também sempre o mesmo). Já calculei a média, é 10,1. Não me serve de nada. Desta vez há 5 colegas com nota melhor que a minha! Já não posso contar com a mediana. Felizmente, houve três colegas que tiraram 7, logo a moda é 7. Chico esperto Ih, ih, ih, desta vez direi ao meu pai que estou acima da moda, e espero que ele não saiba as diferenças entre a média, moda e a mediana!

85. Ficha de trabalho FIM

86. Existe mais do que um processo para determinar os quartis quando o número de dados é ímpar. Podemos optar por qualquer um destes processos, apesar dos valores obtidos serem diferentes (repara no entanto que os valores são aproximados). Exercícios da página 83.

87. Num diagrama de extremos e quartis existem características que permitem avaliar o grau de simetria ou enviesamento da distribuição e a sua maior ou menor concentração: os comprimentos da caixa e das linhas que saem da caixa (“os bigodes”), e a distância da mediana aos 1.º e 3.º quartis. Enviesamento para a esquerda Enviesamento para a direita Dados simétricos