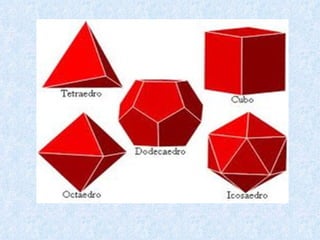
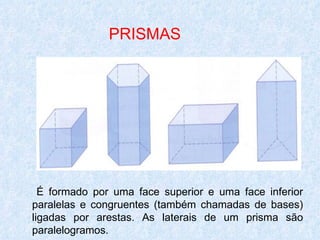
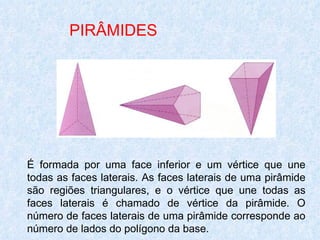
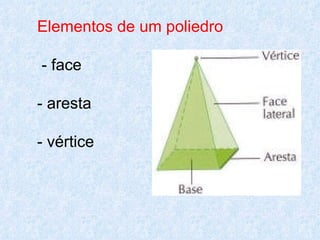
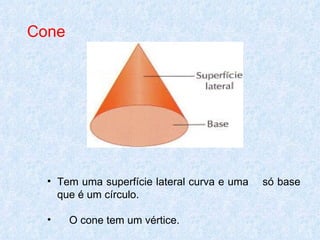
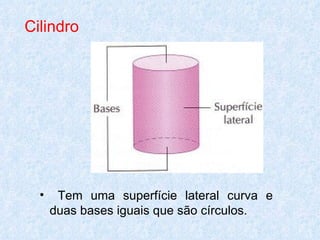
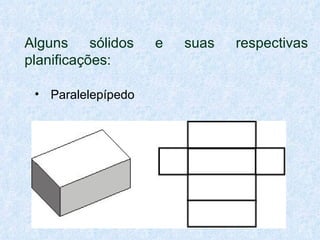
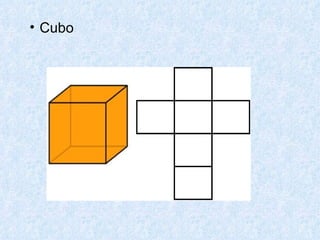
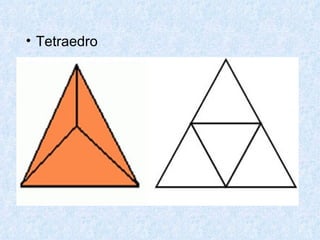
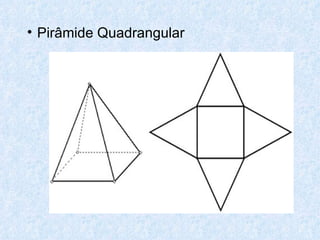
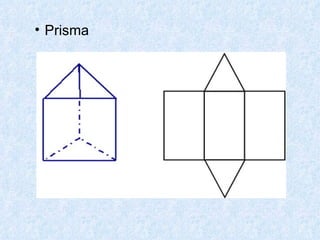
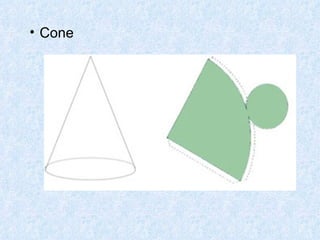
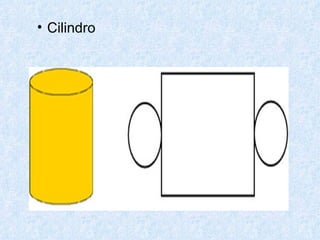
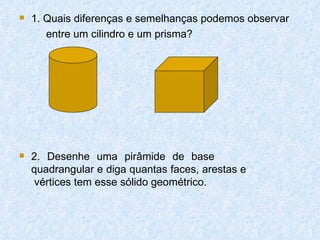
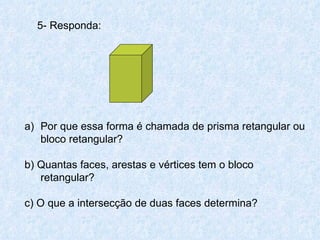
O documento discute os diferentes tipos de sólidos geométricos, divididos em poliedros e não poliedros. Os poliedros incluem figuras como cubos, pirâmides e prismas, cujas faces são polígonos. Os não poliedros como esferas, cones e cilindros têm pelo menos uma face curva. Exemplos comuns de cada tipo de sólido são dados, com suas características e elementos definidos.