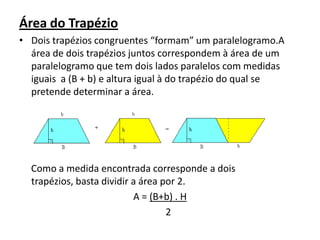
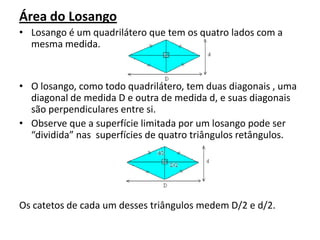
O documento explica os métodos para calcular as áreas e perímetros de várias figuras planas como retângulos, quadrados, paralelogramos, trapézios, triângulos e losangos. Inicialmente, descreve a evolução das unidades de medida e a criação do sistema métrico decimal. Em seguida, apresenta as fórmulas para calcular áreas e perímetros de cada figura plana e exemplos ilustrativos.

1. Objeto de Aprendizagem:Áreas e Perímetros de Figuras PlanasAluna:Fabiana Candida Accorinte Maia

2. Um pouco da história... Nem sempre a unidade de medida escolhida pelo homem, forneceu um único resultado numérico.O palmo, o pé, o passo, dentre outros, variavam de pessoa para pessoa.Ao longo da evolução, as unidades para medir comprimentos e superfícies variavam em diversas partes do mundo e isso gerou alguns problemas, principalmente comerciais.

3. Para acabar com esses problemas, no final do século XVIII, na frança, em plena Revolução Francesa, foi criada uma comissão de cientistas e matemáticos que estabeleceram um sistema universal de medidas: o sistema métrico decimal.A unidade de medida de comprimento é o metro, que se abrevia m, e a unidade fundamental da superfície é o metro quadrado, que se abrevia m².

4. Perímetro e Área Para calcular o perímetro de um quadrado de um metro de lado, basta somar a medida de todos os seus lados. Assim: 1m + 1m + 1m + 1m = 4m.E a área desse quadrado é 1m².

5. RetânguloPara todo e qualquer retângulo de base(b) e altura (h), pode-se escrever:Área do Retângulo = medida da base (b) x medida da altura (h)A = b. h Exemplo:Determine a área e o perímetro de uma cozinha que tem 4m de comprimento e 2m de largura. A = 4m x 2m P = 4m + 4m + 2m + 2m A = 8m² P = 12m

6. QuadradoO Quadrado é um retângulo cuja base e altura têm medidas iguais. Exemplo: Determine a área e o perímetro de uma praça quadrada sabendo que seu lado mede 45m A = 45m x 45m P = 45m + 45m + 45m + 45m A = 2.025 m² P = 180 m

7. Área do ParalelogramoTodo paralelogramo pode ser decomposto para compor um retângulo.Área do paralelogramo = medida da base(b) x medida da altura(h) A = b . h Exemplo: Calcule a área e o perímetro de um paralelogramo com 5cm de base e 1,5cm de altura. A = 5cm x 1,5cm P = 5cm + 5cm + 1,5cm + 1,5cm A = 7,5 cm² P = 13 cm

8. Área do TrapézioDois trapézios congruentes “formam” um paralelogramo.A área de dois trapézios juntos correspondem à área de um paralelogramo que tem dois lados paralelos com medidas iguais a (B + b) e altura igual à do trapézio do qual se pretende determinar a área. Como a medida encontrada corresponde a dois trapézios, basta dividir a área por 2.A = (B+b) . H 2

9. Exemplo:Num trapézio, as bases medem 20cm e 12cm, e a altura mede 6cm.Determine a área do trapézio. A = (20 + 12). 6 = 96 cm² 2Área do Triângulo A área de um triângulo qualquer de base(b) e altura (h) pode ser determinada da seguinte forma:Área do triângulo = medida da base (b) x medida da altura(h) 2A = b.h 2

10. Área do LosangoLosango é um quadrilátero que tem os quatro lados com a mesma medida.O losango, como todo quadrilátero, tem duas diagonais , uma diagonal de medida D e outra de medida d, e suas diagonais são perpendiculares entre si. Observe que a superfície limitada por um losango pode ser “dividida” nas superfícies de quatro triângulos retângulos.Os catetos de cada um desses triângulos medem D/2 e d/2.

11. Assim, a área do losango pode ser dada pela área de um triângulo retângulo multiplicada por 4. Área do Losango = Exemplo: Determine a área de um losango sabendo que a sua diagonal maior mede 12cm e sua diagonal menor, 8cm.

12. Referências:Apostila de Matemática do CoC,7°Ano – Ensino Fundamental,2010.http://www.mundoeducacao.com.br/matematica/area-losango.htm