O documento apresenta um resumo de um curso introdutório sobre álgebra matricial, abordando tópicos como espaços vetoriais, transformações lineares e métodos numéricos. É introduzido o conceito de matrizes e operações matriciais, como soma, subtração, multiplicação por escalar e produto. Propriedades como transposta, traço e inversa também são explicadas.

1. Aula 1
UFBA
10/07/2021

2. O curso
Introdução à álgebra matricial
Espaços vetoriais
Transformações lineares
Métodos numéricos

3. O curso
Introdução à álgebra matricial
Espaços vetoriais
Transformações lineares
Métodos numéricos
Bibliografia
Anton, H., & Rorres, C. (2001). Álgebra linear com aplicações (Vol.
8). Bookman.
Gentle, J. E. (2007). Matrix algebra: theory, computations, and
applications in statistics. Springer Science & Business Media.

4. Matrizes
Para resolver o sistema de equações lineares
�
5x + y = 3
2x − y = 4

5. Matrizes
Para resolver o sistema de equações lineares
�
5x + y = 3
2x − y = 4
�





a11 a12 · · · a1n
a21 a22 · · · a2n
.
.
.
.
.
.
...
.
.
.
am1 am2 · · · amn





= A

6. Uma matriz A, m×n (m por n), é uma tabela de mn números dispostos
em m linhas e n colunas.
Exemplos:
�
1 2 3
4 5 6
�


2
−3
0

 [10]
�
1 0, 3 π e
−102
√
2 0 2
�

7. A = [aij ]m×n = [aij ] = (aij ) e aij = (A)ij
Uma matriz de tamanho n × n é dita matriz quadrada de ordem n:
A =





a11 a12 · · · a1n
a21 a22 · · · a2n
.
.
.
.
.
.
...
.
.
.
an1 an2 · · · ann





A e B são iguais se tiverem o mesmo tamanho e suas entradas
correspondentes forem iguais:
Se A = [aij ] e B = [bij ] têm o mesmo tamanho, então são iguais se
aij = bij para todo i = 1, . . . , m e j = 1, . . . , n.

9. Notação
Mm×n(R) = {matrizes m × n com entradas reais}
Mn(R) = {matrizes quadradas de ordem n}
Matriz identidade de ordem n:
In =





1 0 0 · · · 0
0 1 0 · · · 0
.
.
.
.
.
.
.
.
.
...
.
.
.
0 0 0 · · · 1





Matriz nula de tamanho m × n:
0m×n =



0 0 0 · · · 0
.
.
.
.
.
.
.
.
.
...
.
.
.
0 0 0 · · · 0




10. Operações matriciais: Sejam A = [aij ] e B = [bij ] matrizes do
mesmo tamanho
A soma A + B é a matriz obtida somando as entradas
correspondentes de A e B:
A + B = [aij + bij ]

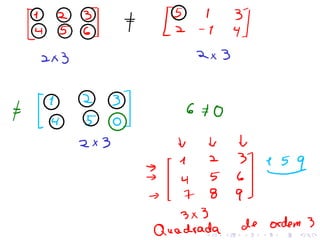
11. Operações matriciais: Sejam A = [aij ] e B = [bij ] matrizes do
mesmo tamanho
A soma A + B é a matriz obtida somando as entradas
correspondentes de A e B:
A + B = [aij + bij ]
A diferença A − B é a matriz obtida subtraindo as entradas de B
das entradas correspondentes de A:
A − B = [aij − bij ]

12. Operações matriciais: Sejam A = [aij ] e B = [bij ] matrizes do
mesmo tamanho
A soma A + B é a matriz obtida somando as entradas
correspondentes de A e B:
A + B = [aij + bij ]
A diferença A − B é a matriz obtida subtraindo as entradas de B
das entradas correspondentes de A:
A − B = [aij − bij ]
Se c é um escalar qualquer, a multiplicação por um escalar cA é a
matriz obtida pela multiplicação de cada entrada de A por c:
cA = [caij ]

13. Exemplos: Dadas A =
�
2 3 4
1 3 1
�
e B =
�
0 2 7
−1 3 −5
�
,
determine A + B, (−1)A, B + 2A.

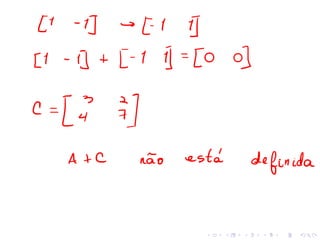
15. Sejam A = [aij ]m×p e B = [bij ]p×n, o produto AB é a matriz de
tamanho m × n cuja entrada ij é a soma dos produtos dos
elementos da i-ésima linha de A pelos elementos correspondentes da
j-ésima coluna de B:
(AB)ij = ai1b1j + ai2b2j + · · · + aipbpj

16. Sejam A = [aij ]m×p e B = [bij ]p×n, o produto AB é a matriz de
tamanho m × n cuja entrada ij é a soma dos produtos dos
elementos da i-ésima linha de A pelos elementos correspondentes da
j-ésima coluna de B:
(AB)ij = ai1b1j + ai2b2j + · · · + aipbpj
AB =





a11 a12 · · · a1p
a21 a22 · · · a2p
.
.
.
.
.
.
...
.
.
.
am1 am2 · · · amp





m×p
·





b11 b12 · · · b1n
b21 b22 · · · b2n
.
.
.
.
.
.
...
.
.
.
bp1 bp2 · · · bpn





p×n

17. Exemplos: Dadas A =
�
1 2 −3
3 4 0
�
e B =


−2 1 0
0 3 −1
5 −4 0

,
determine AB.

19. Seja A = [aij ], definimos a sua transposta como sendo a matriz
AT = [bij ], onde bij = aji .

20. Seja A = [aij ], definimos a sua transposta como sendo a matriz
AT = [bij ], onde bij = aji .
Se A = [aij ] é uma matriz quadrada, definimos o traço de A como
sendo a soma dos entradas na diagonal principal de A:
tr(A) = a11 + a22 + · · · + ann

21. Exemplos: Dadas A =
�
−2 1 0
4 0 π
�
e B =


1 2 3
4 5 6
7 8 9

, determine
AT , BT e tr(B).

22. Propriedades da aritmética matricial
A + B = B + A
A + (B + C) = (A + B) + C
A(BC) = (AB)C
A(B + C) = AB + AC
a(A + B) = aA + aB
(AT )T = A
(A + B)T = AT + BT
(AB)T = BT AT

24. Inversa de uma matriz
Seja A uma matriz quadrada de ordem n, dizemos que A é invertı́vel se
existe uma matriz B também de ordem n tal que AB = BA = In.

25. Inversa de uma matriz
Seja A uma matriz quadrada de ordem n, dizemos que A é invertı́vel se
existe uma matriz B também de ordem n tal que AB = BA = In.
Uma tal matriz B, quando existe, é chamada de matriz inversa de A
Se não existe uma tal B, A é dita não invertı́vel
Dizemos que A e B são inversas entre si

26. A matriz A =
�
a b
c d
�
é invertı́vel se e somente se ad −bc �= 0. Neste
caso,
A−1
=
1
ad − bc
�
d −b
−c a
�

27. Exemplos: Determine, quando possı́vel, a inversa das matrizes
A =
�
1 1
4 2
�
e B =
�
−1 2
3 −6
�
.

28. Propriedades: Se A e B são matrizes invertı́veis do mesmo tamanho,
então
AB é invertı́vel e (AB)−1 = B−1A−1
A−1 é invertı́vel e (A−1)−1 = A
AT é invertı́vel e (AT )−1 = (A−1)T
se n é um número natural, então An = A · A · · · A é invertı́vel e
(An)−1 = (A−1)n
se k é um número real não nulo, então kA é invertı́vel e
(kA)−1 =
1
k
A−1

29. Algoritmo da inversão
Se a matriz quadrada A é invertı́vel, construimos a matriz [A| I ] e através
de operações elementares a transformamos numa matriz da forma [ I |B].
Então A−1 = B.

30. Algoritmo da inversão
Se a matriz quadrada A é invertı́vel, construimos a matriz [A| I ] e através
de operações elementares a transformamos numa matriz da forma [ I |B].
Então A−1 = B.
Operações elementares com as linhas de uma matriz
Multiplicar uma linha por uma constante não nula
Trocar duas linhas entre si
Somar uma constante vezes uma linha a uma outra linha

31. Exemplos: Determine a matriz inversa de A =


1 1 0
0 2 1
1 0 1

.

34. Uma matriz quadrada A é invertı́vel se, e somente se, det(A) �= 0.