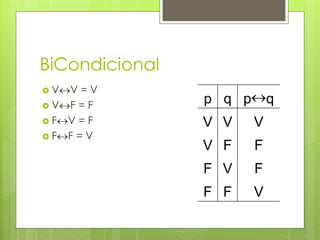
O documento discute os operadores lógicos condicional e bicondicional. Explica que o condicional (p → q) representa "se p então q" e que p é o antecedente e q é o consequente. O bicondicional (p ↔ q) representa "p se e somente se q" e ambos p e q devem ser verdadeiros ou falsos.

1. Lógica Matemática
Aula 04

2. Condicional()

3. Condicional
Chama-se proposição condicional uma proposição representada por “se p então q”.
pq
Se p então q
p implica q

4. Condicional
pq
p é antecedente
q é consequente

5. Condicional
pq
p é condição suficiente para q
q é condição necessária para p

6. Condicional
pq
Se p então q;
p implica em q;
p somente se q;
p é condição suficiente para q;
q é condição necessária para p.

7. Condicional
Se amanhã é domingo, então hoje é sábado.
Se eu estudo, então obtenho uma boa nota na prova.
Se está chovendo, então existem nuvens.
Se João vai à Igreja, então João é uma boa pessoa.

8. Condicional
Se está chovendo, então existem nuvens.
p: Está chovendo.
q: Existem nuvens.
Estar chovendo implica existir nuvens.
Está chovendo somente se existem nuvens.
Estar chovendo é condição suficiente para existir nuvens.
Existir nuvens é necessário para estar chovendo.

9. Condicional
Se está chovendo então existem nuvens.
Estar chovendo (A) é condição suficiente para existir nuvens (B).
Basta que A seja verdade para B também ser verdade.

10. Condicional
Se está chovendo então existem nuvens.
Existir nuvens (B) é condição necessária para estar chovendo (A).

11. Condicional
Quando uma condicional é verdadeira?
Se está chovendo então existem nuvens.
A condicional é verdadeira quando a verdade do antecedente implica na verdade do consequente.
V → V = V

12. Condicional
Quando uma condicional é falsa?
Se está chovendo então existem nuvens.
A condicional é falsa quando a verdade do antecedente não implica na verdade do consequente.
V → F = F

13. Condicional
E as outras situações? Quando o antecedente é falso?
Se está chovendo então existem nuvens.
A condicional só afirma a relação entre consequente e antecedente, quando o antecedente é verdadeiro.
Se o antecedente é falso não temos como mostrar que a condicional é falsa.
F → V = V
F → F = V

14. Condicional
VV = V
VF = F
FV = V
FF = V
p
q
pq
V
V
V
V
F
F
F
V
V
F
F
V

15. Condicional
VV = V
Se de fato a verdade de p se fizer seguir da de q, ou seja, se p for de fato suficiente para q, a implicação é verdadeira.
p
q
pq
V
V
V
V
F
F
F
V
V
F
F
V

16. Condicional
VF = F
p não é suficiente para q, assim, a implicação é falsa.
p
q
pq
V
V
V
V
F
F
F
V
V
F
F
V

17. Condicional
FV = V
FF = V
p não é satisfeito, é falso. Tanto q sendo V ou F, tornam a implicação verdadeira.
p
q
pq
V
V
V
V
F
F
F
V
V
F
F
V

18. Condicional
p: João é engenheiro.
q: João sabe matemática.
p  q
Se João é engenheiro
então sabe matemática.
p
q
pq
V
V
V
V
F
F
F
V
V
F
F
V

19. Condicional
Se João vai à igreja, então João é uma boa pessoa.
O que seria necessário para mostrar que essa afirmação é falsa?

20. BiCondicional()

21. BiCondicional
Chama-se proposição bicondicional uma proposição representada por “p se e somente se q”, cujo valor lógico é a verdade (V) quando p e q são ambas verdadeiras ou ambas falsas, e a falsidade (F) nos demais casos.
p se e somente se q
p  q

22. BiCondicional
p  q
p é condição necessária e suficiente para q
q é condição necessária e suficiente para p
(p  q) ∧ (q  p)

23. BiCondicional
VV = V
VF = F
FV = F
FF = V
p
q
pq
V
V
V
V
F
F
F
V
F
F
F
V

24. BiCondicional
João é careca, se e somente se, João não tem cabelo.
p: João é careca.
q: João não tem cabelo.
pq:
Se João é careca, então João não tem cabelo e
Se João não tem cabelo, então João é careca.

25. BiCondicional
p: João é careca.
q: João não tem cabelo.
pq
p
q
pq
V
V
V
V
F
F
F
V
F
F
F
V

26. Ordem de precedência
Negação (~)
Conjunção
Disjunção
Condicional
Bicondicional

27. Ordem de precedência
p  q  r
(p  (q  r))
Bicondicional
p ∨ ~q  q ∧ r
p ∨ (~q)  q ∧ r
((p ∨ (~q)) ( q ∧ r ))
Condicional

28. Tabela Verdade
http://www.calculadoraonline.com.br/tabela-verdade