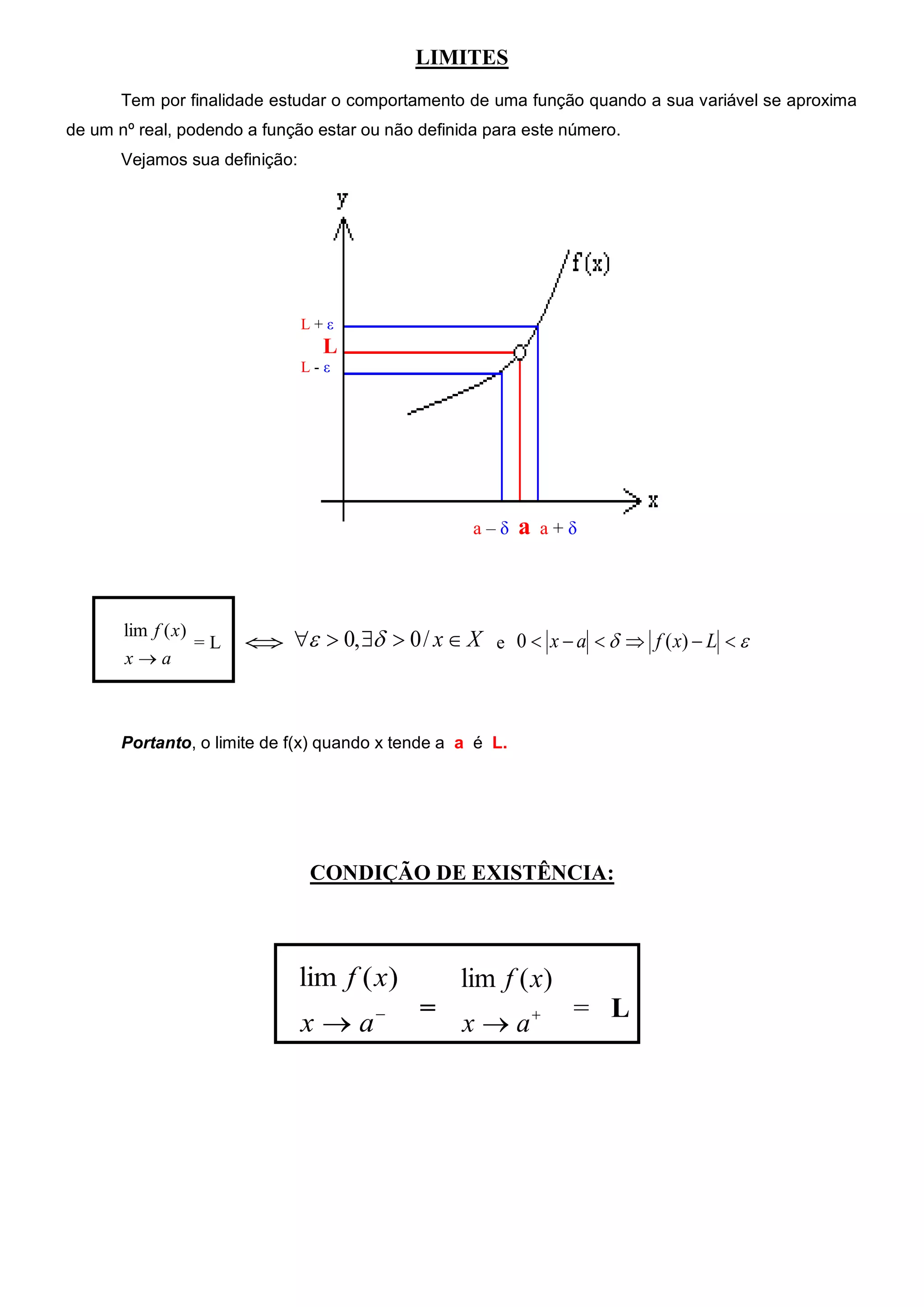
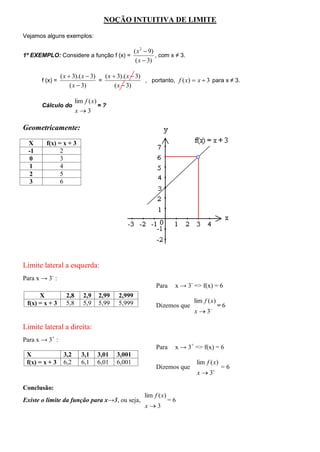
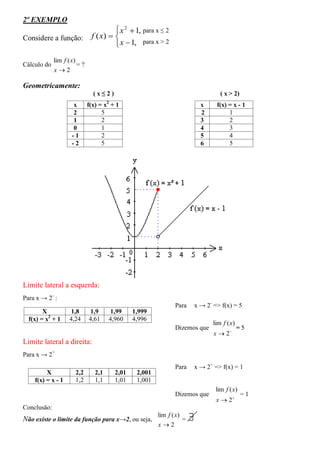
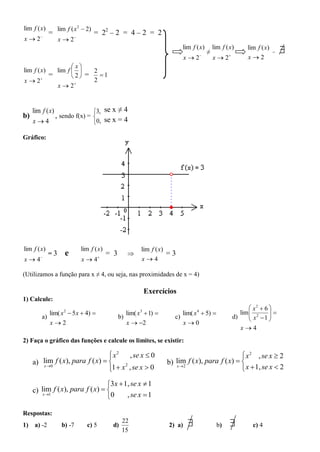
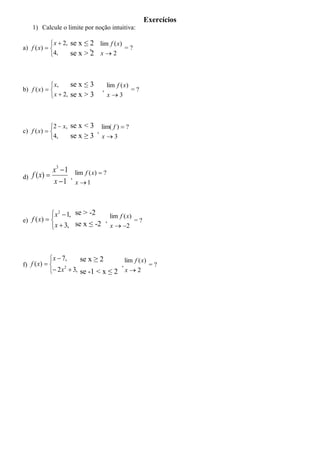1) O documento discute limites de funções, definindo-os formalmente como a aproximação do comportamento de uma função quando sua variável se aproxima de um número real. 2) Apresenta exemplos numéricos e gráficos para ilustrar o cálculo de limites laterais esquerdo e direito. 3) Lista propriedades algébricas dos limites, como a soma, produto e quociente de limites.

1. LIMITES
Tem por finalidade estudar o comportamento de uma função quando a sua variável se aproxima
de um nº real, podendo a função estar ou não definida para este número.
Vejamos sua definição:
L+ε
L
L-ε
a–δ a a+δ
   0,   0 / x  X e 0  x  a    f ( x)  L  
lim f ( x)
=L
xa
Portanto, o limite de f(x) quando x tende a a é L.
CONDIÇÃO DE EXISTÊNCIA:
lim f ( x) lim f ( x)
= = L
x  a x  a

2. NOÇÃO INTUITIVA DE LIMITE
Vejamos alguns exemplos:
( x 2  9)
1º EXEMPLO: Considere a função f (x) = , com x ≠ 3.
( x  3)
( x  3).( x  3) ( x  3).( x  3)
f (x) = = , portanto, f ( x)  x  3 para x ≠ 3.
( x  3) ( x  3)
lim f ( x)
Cálculo do =?
x3
Geometricamente:
X f(x) = x + 3
-1 2
0 3
1 4
2 5
3 6
Limite lateral a esquerda:
Para x → 3- :
Para x → 3- => f(x) = 6
X 2,8 2,9 2,99 2,999
f(x) = x + 3 5,8 5,9 5,99 5,999 lim f ( x)
Dizemos que =6
x  3
Limite lateral a direita:
Para x → 3+ :
Para x → 3+ => f(x) = 6
X 3,2 3,1 3,01 3,001
f(x) = x + 3 6,2 6,1 6,01 6,001 lim f ( x)
Dizemos que =6
x  3
Conclusão:
lim f ( x)
Existe o limite da função para x→3, ou seja, =6
x3

3. 2º EXEMPLO
 x 2  1, para x ≤ 2
Considere a função: f ( x)  
 x  1, para x > 2
lim f ( x)
Cálculo do =?
x2
Geometricamente:
(x≤2) ( x > 2)
x f(x) = x2 + 1 x f(x) = x - 1
2 5 2 1
1 2 3 2
0 1 4 3
-1 2 5 4
-2 5 6 5
Limite lateral a esquerda:
Para x → 2- :
Para x → 2- => f(x) = 5
X 1,8 1,9 1,99 1,999
f(x) = x2 + 1 4,24 4,61 4,960 4,996
lim f ( x)
Dizemos que =5
x  2
Limite lateral a direita:
Para x → 2+
Para x → 2+ => f(x) = 1
X 2,2 2,1 2,01 2,001
f(x) = x - 1 1,2 1,1 1,01 1,001
lim f ( x)
Dizemos que =1
x  2
Conclusão:
Não existe o limite da função para x→2, ou seja,
lim f ( x)
= 
x2

4. Exercícios
1) Calcule o limite por noção intuitiva:
 x  2, se x ≤ 2 lim f ( x)
a) f ( x)   , =?
4, se x > 2 x  2
 x, se x ≤ 3 lim f ( x)
b) f ( x)   , =?
 x  2, se x > 3 x3
2  x, se x < 3 lim( f )  ?
c) f ( x)   ,
4, se x ≥ 3 x  3
x3  1 lim f ( x)  ?
d) f ( x)  ,
x 1 x 1
 x 2  1, se > -2 lim f ( x)
e) f ( x)   , =?
 x  3, se x ≤ -2 x  2
 x  7, se x ≥ 2 lim f ( x)
f) f ( x)   , =?
 2 x  3, se -1 < x ≤ 2 x2
2

5. TEOREMAS DOS LIMITES (PROPRIEDADES)
Vamos mostrar agora alguns teoremas que admitiremos verdadeiros sem efetuarmos suas demonstrações.
1. Limite da função constante: o limite de uma constante é a própria constante, isto é,
lim c  c
x a
EXEMPLOS:
lim 2
a) f ( x)  2 => =2
x 1
b) f ( x)  5 => lim 5  5
x0
c) f ( x)  3 => lim  3  3
x 2
2. Limite da função identidade: se f ( x)  x , então:
lim x  a
x a
EXEMPLOS:
a) lim x  2
x 2
b) lim x  3
x 3
3. Limite da soma de funções: é igual à soma dos limites dessas funções.
lim  f1( x)  f 2 ( x)   f n ( x)  lim f1( x) lim f 2 ( x)  lim f n ( x)
x a x a x a
EXEMPLO:
lim( x  3)  lim x  lim 3  2  3  5
x 2 x 2 x 2
4. Limite do produto de funções: é igual ao produto dos limites dessas funções.
lim  f1( x). f 2 ( x)   f n ( x)  lim f1( x). lim f 2 ( x)   lim f n ( x)
x a x a x a
EXEMPLO:
lim 3.( x  1)  lim 3. lim( x  1)  3.3  9
x 2 x 2 x 2
5. Limite da constante multiplicada pela função: é igual ao produto da constante pelo limite da
função.
lim c. f ( x)  c. lim( x)
x a x a

6. EXEMPLO:
lim 3x  3.lim x  3.2  6
x 2 x 2
6. Limite de uma potência enésima de uma função: é igual à potência enésima do limite dessa
função.
n
lim  f ( x)   lim f ( x) 
n
x a  x a
 

EXEMPLO:
  2 8
3
lim x3  lim x 3
x 2 x 2
7. Limite de uma raiz enésima de uma função: é igual à raiz enésima do limite dessa função.
lim n f ( x)  n lim f ( x)
x a x a
EXEMPLOS:
a) lim x lim x  100  10
x 100 x 100
b) lim
5
2 x 4  5 lim 2 x 4  5 2.24  5 32  2
x 2 x 2
8. Limite do módulo ou valor absoluto de uma função: é igual ao módulo ou valor absoluto
do limite.
lim f ( x)  lim f ( x)
x a x a
EXEMPLO:
lim x  lim x  3  3
x 3 x 3
9. Limite do quociente de duas funções: é o quociente dos limites dessas funções (exceto quando
o limite do denominador for igual a zero).
f ( x) x  a f ( x)
lim
lim  ,
x a g ( x) lim g ( x)
xa
com lim g ( x)  0 e g ( x)  0
x a
EXEMPLO:
x x 8 x 8
lim
lim   4
x 8 2 lim 2 2
x 8

7. CÁLCULO DE LIMITE DE FUNÇÃO POLINOMIAL
n 1
Dado o polinômio P( x)  an x  an 1x
n
 ...  a1x  a0 , então lim P( x)  P(a)
x a
EXEMPLOS:
1) Calcule os limites:
lim( x5  2 x3  x)
a) = 15 + 2 . 13 – 1 = 1 + 2 – 1 = 2
x 1
b) lim( x  3)  2  3  5
x 2
lim( x 2  x  2) 2
c) = ( 32 – 3 + 2 )2 = ( 9 – 3 + 2 )2 = ( 6 + 2 )2 = ( 8 )2 = 64
x3
2) Calcule os limites, se existir, e faça um esboço do gráfico.
 x 2  2, se x < 2
lim f ( x) 
a) , sendo f(x) =  x se x ≥ 2
x2  ,
2
Gráfico:
(x<2) ( x ≥ 2)
x
x f(x) = x2 - 2 x f(x) =
2
2 2 2 1
3
1 -1 3 = 1,5
2
0 -2 4 2
5
-1 -1 5 = 2,5
2

8. lim f ( x) lim f ( x 2  2)

= = 22 – 2 = 4 – 2 = 2
x2 x  2
lim f ( x)
≠
lim f ( x) lim f ( x)
= 
x2 
x2 
x2
 x
lim f ( x) lim f   2
= 2 = 1
x  2 2
x  2
lim f ( x) 3, se x ≠ 4
b) , sendo f(x) = 
x4 0, se x = 4
Gráfico:
lim f ( x) lim f ( x) lim f ( x)
=3 e = 3  =3
x4 
x4 
x4
(Utilizamos a função para x ≠ 4, ou seja, nas proximidades de x = 4)
Exercícios
1) Calcule:
 x2  6 
lim( x 2  5 x  4)  lim( x3  1)  lim( x 4  5)  lim  2
 x 1  

a) b) c) d)  
x2 x  2 x0
x4
2) Faça o gráfico das funções e calcule os limites, se existir:
 x2
 , se x  0  x 2 , se x  2
a) lim f ( x), para f ( x)   b) lim f ( x), para f ( x)  
x 0
1  x , se x  0 x 2
 x  1, se x  2
2

3x  1, se x  1
c) lim f ( x), para f ( x)  
x 1
0 , se x  1
Respostas:
1) a) -2 b) -7 c) 5 d)
22
2) a)  b)  c) 4
15

9. CÁLCULO DE LIMITES QUANDO O NUMERADOR E O DENOMINADOR
TENDEM A ZERO
Quando o numerador e o denominador de uma função tender a zero, no cálculo de um limite
para determinado valor de x, devemos efetuar e simplificar a função antes de efetuarmos a substituição,
porque ela não é definida para aquele valor de x.
EXEMPLOS:
x2  9
1) Calcular lim
x 3 x  3
Fatorando e simplificando, temos:
x2  9 ( x  3).( x  3)
lim  lim  lim( x  3)  6
x 3 x  3 x 3 ( x  3) x 3
x 1  3
2) Calcular lim
x 8  x  8
Neste caso devemos multiplicar e dividir a fração pelo conjugado do numerador.
x 1  3 ( x  1  3).( x  1  3)
lim  lim 
x 8  x  8 x 8  x  8.( x  1  3)
( x  1) 2  32 x 1 9
 lim  lim 
x 8  x  8  .( x  1  3) x 8  x  8  .( x  1  3)
 lim
 x  8  lim
1

x 8  x  8  .( x  1  3) x 8 ( x  1  3)
1 1 1
  
( 8  1  3) ( 9  3) 6
x2  5x  6
3) Calcular lim
x 2 x2
Resolvendo a equação x 2  5x  6  0
  b 2  4ac
  25  24  1
 1
 5 1 6
 b    (5)  1  5  1  x1  2  2  3

x   
2a 2  (1) 2 x  5  1  4  2
 2
 2 2
Obtemos duas raízes distintas: x1  3 e x2  2 .
Fatoramos o trinômio do 2º grau: x 2  5x  6  x  3  x  2
x2  5x  6 ( x  2).( x  3)
Então, lim  lim  1
x 2 x2 x 2 x2

10. x3  8
4) Calcular lim
x 2 x  2
Fazendo a divisão de x3  8 por x  2 , para simplificar, temos:
 x  0x  0x  8 x  2
3 2
 x3  2 x 2 x2  2x  4
 2 x2  0 x  8
 2 x2  4 x
 4x  8
 4x  8
0
x3  8
Então, lim  lim( x 2  2 x  4)  22  2.(2)  4  4  4  4  12
x 2 x  2 x 2
Observação:
Poderíamos ter fatorado o numerador pela “diferença de cubos”
a3  b3  (a 2  ab  b2 ).(a  b)
Assim, teríamos:
   
x3  8  x3  23  x 2  2 x  22  x  2  x 2  2 x  4  x  2
x 3  8 x 2  2 x  4 x  2
Depois, simplificaríamos:   x 2  2x  4 
x 2 x2
E, então, calcularíamos o limite desejado:
x3  8
lim  lim( x 2  2 x  4)  22  2.(2)  4  4  4  4  12
x 2 x  2 x 2
x2  5x  6
5) Calcular lim
x 3 x 2  x  12
Fazendo a divisão de polinômios (numerador pelo denominador):
 x 2  5 x  6 x 2  x  12
 x 2  x  12 1
 6 x  18 Resto!

11. Como a divisão não é exata, temos que simplificar a fração algébrica pela fatoração do numerador e do
denominador. Assim:
Resolvendo a equação (numerador): Resolvendo a equação (denominador):
x  5x  6  0
2
x 2  x  12  0
5  25  24 1  1  48
x x
2 2
5  1  x '  3 1  7 x '  4
x  x 
2  x ''  2 2  x ''  3
Fatorando: Fatorando:
x  5x  6  1.( x  3).( x  2)
2
x2  x  12  1.( x  4).( x  3)
Substituindo os trinômios fatorados no limite, temos:
x2  5x  6 ( x  3) .( x  2)
lim 2  lim 
x 3 x  x  12 x 3 ( x  4). ( x  3)
x  2 3  2 1 1
lim   
x 3 x  4 3  4 7 7
2
 x 2  4x  4 
6) Calcular lim  
x 2
 x2 
x 2  4x  4
Fazendo u  , temos que:
x2
lim u  lim
x 2  4x  4
 lim
x  22  lim x  2  0 , logo: lim u  0 ,
x 2 x 2 x2 x 2  x  2  x 2 x 2
então limu   0 2  0
2
x 2
Exercícios
1) Calcule:
x4 x 2 x3  x x 2  16
a) lim b) lim c) lim d) lim
x 4 x 2  16 x 2 x2 x 0 x x 4 x4
Respostas:
1 1
1) a) b) c) - 1 d) 8
8 2 2