Este documento apresenta os conceitos fundamentais de cálculo, como:
1) Limites, definidos como a aproximação de uma função quando sua variável independente tende a um valor;
2) Derivadas, definidas como a razão entre o incremento da função e o incremento da variável independente, representando a taxa de variação da função;
3) Continuidade, relacionada à ausência de descontinuidades no gráfico da função.

![Apostila de Cálculo I
2
Limites
Diz-se que uma variável x tende a um número real a se a diferença em
módulo de x-a tende a zero. ( ax ≠ ). Escreve-se: ax → ( x tende a a).
Exemplo : Se .1,2,3,4,..N,
N
1
x == quando N aumenta, x diminui, tendendo a zero.
Definição:
f(x)lim
ax→
é igual a L se e somente se, dado 0εeax 〉→ , existe 0δ 〉 tal que se
εa-x0 〈〈 então δL-(x)f 〈 .
Propriedades:
constante)C(CC1. lim
ax
==
→
[ ] (x)g(x)f(x)g(x)f2. limlimlim
axaxax →→→
±=±
[ ] (x)g.(x)f(x)g.(x)f.3 limlimlim
axaxax →→→
=
[ ]
n
ax
n
ax
(x)f(x)f4. limlim
=
→→
(x)g
(x)f
(x)g
(x)f
5.
lim
lim
lim
ax
ax
ax
→
→
→
=
n
ax
n
ax
(x)f(x)f.6 limlim →→
=](https://image.slidesharecdn.com/apostiladecalculoi-160817154757/85/Apostila-de-calculo-i-2-320.jpg)

![Apostila de Cálculo I
4
Exercícios :
1) Calcular os limites:
a)
3
4x2
1x
lim +
+
→ x
b) 3
2
2x x1
x2x-8
lim
−
+
→
c)
2
8x3
2x
lim −
−
→ x
d)
( )
x
x-4-2
lim
0x→
e)
2y
8y3
2x
lim
+
+
−→
f)
2-2x
232
1x
lim
+−
→
xx
g)
6-x-2x
103
2
2
2x
lim
−+
→
xx
h)
5-x
23
lim
5x
−−
→
x
i)
3x-
2 23
1x
lim +
−
−→
xx
j)
x-4
7 3
2x
lim
xx −−
→
l)
3-x
273
3x
lim
−
→
x
m) ( )273x2
3x
lim +−
→
x
n) ( ) ( )[ ]13
1x
2.4xlim
−
−→
++ x
o)
2t
65tt2
2x
lim +
++
→
p)
2t
65tt2
2x
lim −
+−
→](https://image.slidesharecdn.com/apostiladecalculoi-160817154757/85/Apostila-de-calculo-i-4-320.jpg)
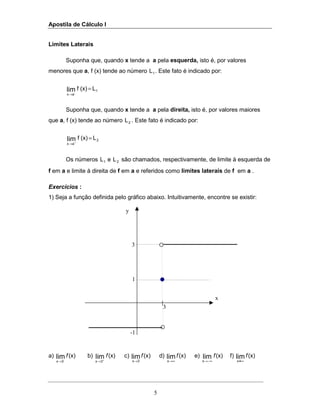




















![Apostila de Cálculo I
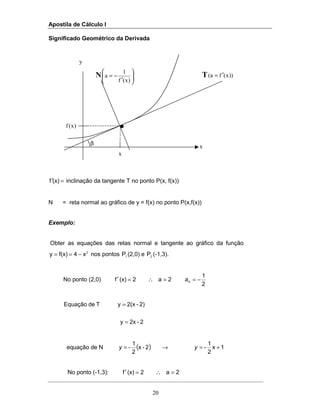
30
Pela Regra da Cadeia: Se uy sec==== ⇒ utguuy ′′′′====′′′′ ..sec
Derivada da função cossecante
xsen
xsen
1
xseccosy 1−
===
( ) ( ) xtgcossecx.co
xsen
cosx
cosxxsen1y
2
2
−=
−
=−=′ −
Pela Regra da Cadeia: Se ug.u .-yuy ′′′′====′′′′⇒⇒⇒⇒==== cotseccosseccos
Exemplos: Calcular as derivadas de:
( )1x2xtgy)1 2
++=
[ ] ( )1x2xsec2x2y 22
+++=′
2)
x
tgx
y
seccos
=
xgxgxg
xfxtgf
cot.seccosseccos
sec
1
2'
−=⇒=
=⇒=
x
gxtgxxxx
y 2
2
'
seccos
cot..seccosseccos.sec +
= =
x
x
seccos
1sec2
+](https://image.slidesharecdn.com/apostiladecalculoi-160817154757/85/Apostila-de-calculo-i-30-320.jpg)

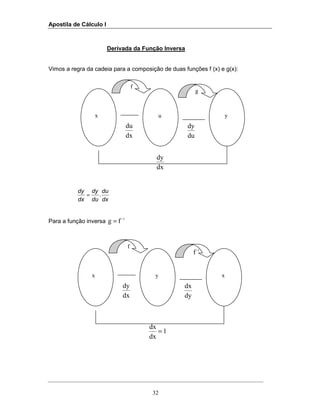


![Apostila de Cálculo I
35
1)
x
2
x
2x
yxlny
2
2
==′⇒=
2)
x2
1
x
x2
1
yxlny ==′⇒=
3)
3ln2
1
3lnx
x2
1
yxlog3 ==′⇒
Lembrar que :
ln (p . q) = ln p + ln q
ln
q
p
= ln p – ln q
ln r
p = r . ln p
Exercícios: Derivar
1) ( )[ ]3
5x4.1-6xlny +=
2) 3
2
2
1x
1x
lny
+
−
=
3)
( )
( )2
32
5x
12xx
lny
+
−
=
4)
−+= 1xxlny 2
5) ( )4xtg.ey -2x
=](https://image.slidesharecdn.com/apostiladecalculoi-160817154757/85/Apostila-de-calculo-i-35-320.jpg)






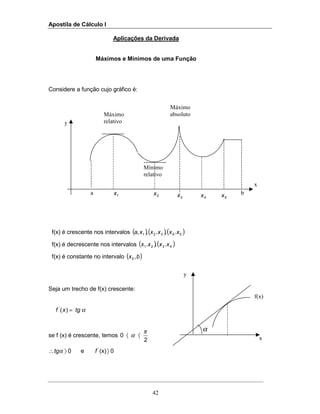





![Apostila de Cálculo I
49
∴=
〉′′⇒=
∴=
〈′′⇒=
=′′
relativomínimodeé
2
13
3,ponto
2
13
(3)f
0(x)f3x
relativomáximodeé
3
20
2,ponto
3
20
(2)f
0(x)f2x
5-x2(x)f
c) inflexão
+∴
==
para-depassa(x)f
2
5
x5-x20(x)f ''
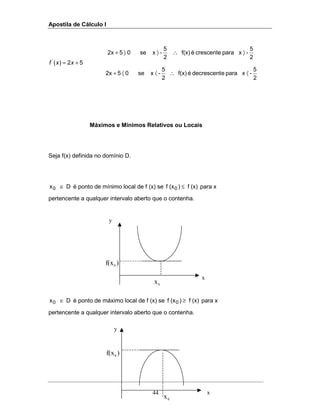
Máximos e Mínimos Absolutos
Se y = f (x) é contínua e definida num intervalo fechado [a,b], derivável em [a,b]
então existem pontos 10 xex tais que:
( ) [ ]
( ) [ ]ba,x,(x)fxf2)
eba,x,(x)fxf)1
1
0
∈∀≤
∈∀≥
0
x = ponto de mínimo absoluto de f(x)
1
x = ponto de máximo absoluto de f(x)
5
2
+](https://image.slidesharecdn.com/apostiladecalculoi-160817154757/85/Apostila-de-calculo-i-49-320.jpg)
![Apostila de Cálculo I
50
Para se obter os pontos de mínimo e máximo absoluto determina-se inicialmente os
pontos de mínimo e máximo relativos. Compara-se esses valores com os da função
no extremo do intervalo.
Exemplo:
Seja 2
x-16(x)fy == no intervalo [ -1, 4 ]
Pontos de máximo e mínimo relativos
[ ]41,-0x0x2-0(x)f'
∈=⇒=⇒=
0xentão0)x(fcomo2)x(f ''''
=〈−= é ponto de máximo local
e o valor máximo da função f (0)=16.
Calculando f (x) nos extremos f (-1)=15 e f (4) =0
Por comparação f (x) = 0 é ponto de máximo absoluto e x =4 é
ponto de mínimo absoluto.
Exercícios:
1) Dada a função 1x9x3
3
x
)x(fy 2
3
++−== verifique os intervalos
para os quais a função é crescente e decrescente. Determine os
pontos críticos, verificando se são de máximo ou mínimo.
Determine o ponto de inflexão, se houver.
2) Idem para x5x3
3
x
)x(fy 2
3
−+−==
3) Determinar números positivos x e y,cujo produto seja igual a 12 e
cuja soma seja a menor possível.
4) Determinar números positivos x e y,cuja soma seja igual a 12 e
cujo produto seja o maior possível.
5) Encontre os pontos críticos, indicando se são máximos ou mínimos
locais para ( )32
1xy −= .](https://image.slidesharecdn.com/apostiladecalculoi-160817154757/85/Apostila-de-calculo-i-50-320.jpg)
