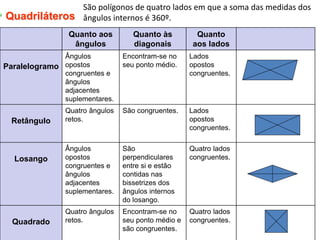
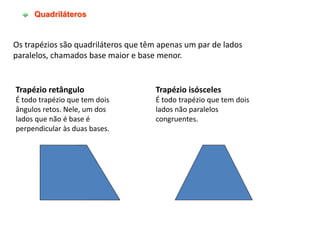
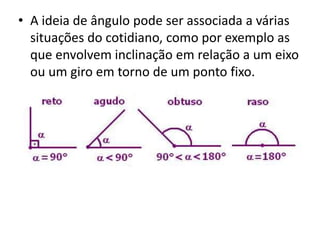
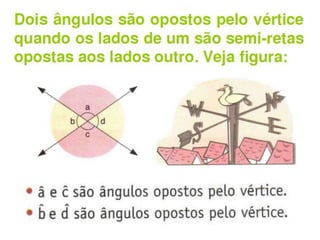
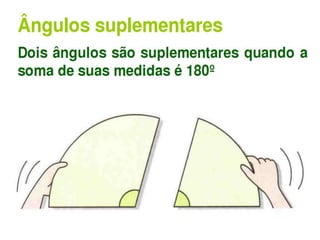
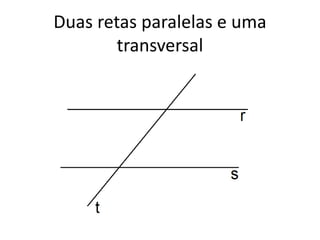
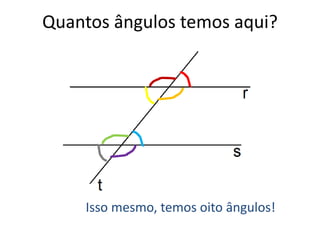
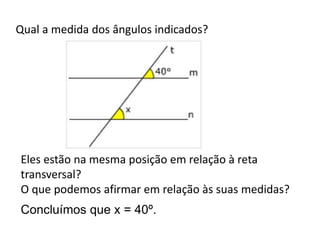
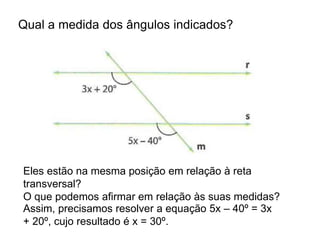
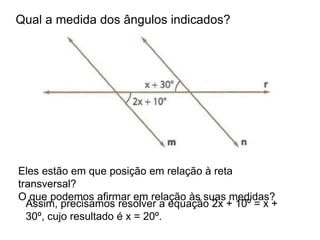
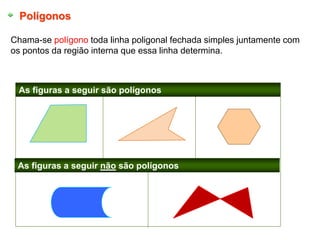
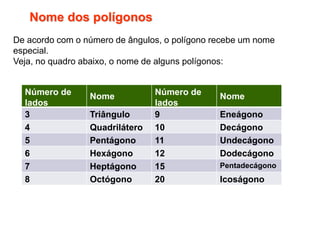
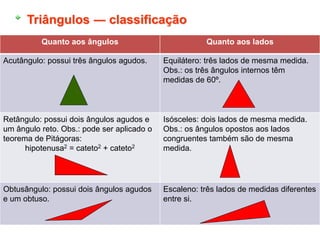
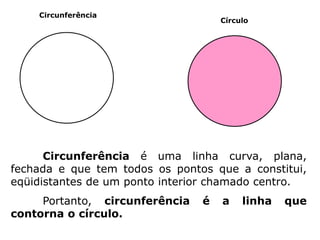
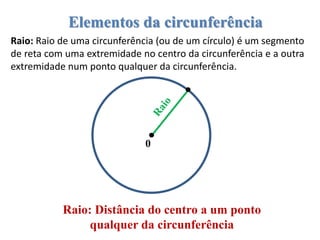
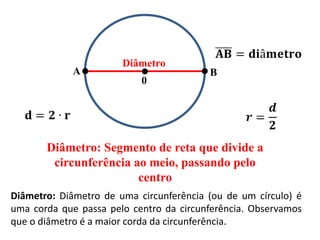
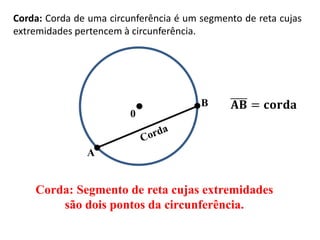
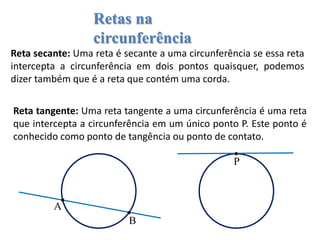
O documento discute conceitos básicos de geometria, incluindo: 1) A origem do termo "geometria" e seu desenvolvimento inicial pelos egípcios e outras civilizações antigas. 2) Elementos básicos da geometria plana como ponto, reta e plano. 3) Conceitos relacionados a circunferências e círculos como raio, diâmetro e corda.

1. AULA 4
MATEMÁTICA

2. A palavra “geometria” vem do grego “geometrien” onde
“geo” significa terra e “metrien” medida. Geometria foi, em sua
origem, a ciência de medição de terras.
O historiador grego Heródoto (500 a.C.) atribuiu aos egípcios
o início da geometria, mas outras civilizações antigas (babilônios,
hindus, chineses) também possuíam muitas informações
geométricas.
A geometria plana, também chamada geometria elementar ou
Euclidiana, teve início na Grécia antiga. Esse estudo analisava as
diferentes formas de objetos, e baseia-se em três conceitos básicos:
ponto, reta e plano.

3. Circunferência é uma linha curva, plana,
fechada e que tem todos os pontos que a constitui,
eqüidistantes de um ponto interior chamado centro.
Portanto, circunferência é a linha que
contorna o círculo.
Círculo
Circunferência

4. Raio: Raio de uma circunferência (ou de um círculo) é um segmento
de reta com uma extremidade no centro da circunferência e a outra
extremidade num ponto qualquer da circunferência.
Elementos da circunferência
0
Raio: Distância do centro a um ponto
qualquer da circunferência

5. Diâmetro
0
Diâmetro: Segmento de reta que divide a
circunferência ao meio, passando pelo
centro
A B
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é
uma corda que passa pelo centro da circunferência. Observamos
que o diâmetro é a maior corda da circunferência.

6. Corda: Corda de uma circunferência é um segmento de reta cujas
extremidades pertencem à circunferência.
0
Corda: Segmento de reta cujas extremidades
são dois pontos da circunferência.
A
B

7. Retas na
circunferência
Reta secante: Uma reta é secante a uma circunferência se essa reta
intercepta a circunferência em dois pontos quaisquer, podemos
dizer também que é a reta que contém uma corda.
Reta tangente: Uma reta tangente a uma circunferência é uma reta
que intercepta a circunferência em um único ponto P. Este ponto é
conhecido como ponto de tangência ou ponto de contato.
B
A
P

8. Polígonos
Chama-se polígono toda linha poligonal fechada simples juntamente com
os pontos da região interna que essa linha determina.
As figuras a seguir são polígonos
As figuras a seguir não são polígonos

9. Nome dos polígonos
De acordo com o número de ângulos, o polígono recebe um nome
especial.
Veja, no quadro abaixo, o nome de alguns polígonos:
Número de
lados
Nome Número de
lados
Nome
3 Triângulo 9 Eneágono
4 Quadrilátero 10 Decágono
5 Pentágono 11 Undecágono
6 Hexágono 12 Dodecágono
7 Heptágono 15 Pentadecágono
8 Octógono 20 Icoságono

10. Triângulos ― classificação
Quanto aos ângulos Quanto aos lados
Acutângulo: possui três ângulos agudos. Equilátero: três lados de mesma medida.
Obs.: os três ângulos internos têm
medidas de 60º.
Retângulo: possui dois ângulos agudos e
um ângulo reto. Obs.: pode ser aplicado o
teorema de Pitágoras:
hipotenusa2 = cateto2 + cateto2
Isósceles: dois lados de mesma medida.
Obs.: os ângulos opostos aos lados
congruentes também são de mesma
medida.
Obtusângulo: possui dois ângulos agudos
e um obtuso.
Escaleno: três lados de medidas diferentes
entre si.

11. Quadriláteros
Quanto aos
ângulos
Quanto às
diagonais
Quanto
aos lados
Paralelogramo
Ângulos
opostos
congruentes e
ângulos
adjacentes
suplementares.
Encontram-se no
seu ponto médio.
Lados
opostos
congruentes.
Retângulo
Quatro ângulos
retos.
São congruentes. Lados
opostos
congruentes.
Losango
Ângulos
opostos
congruentes e
ângulos
adjacentes
suplementares.
São
perpendiculares
entre si e estão
contidas nas
bissetrizes dos
ângulos internos
do losango.
Quatro lados
congruentes.
Quadrado
Quatro ângulos
retos.
Encontram-se no
seu ponto médio e
são congruentes.
Quatro lados
congruentes.
São polígonos de quatro lados em que a soma das medidas dos
ângulos internos é 360º.

12. Quadriláteros
Os trapézios são quadriláteros que têm apenas um par de lados
paralelos, chamados base maior e base menor.
Trapézio retângulo
É todo trapézio que tem dois
ângulos retos. Nele, um dos
lados que não é base é
perpendicular às duas bases.
Trapézio isósceles
É todo trapézio que tem dois
lados não paralelos
congruentes.

13. • A ideia de ângulo pode ser associada a várias
situações do cotidiano, como por exemplo as
que envolvem inclinação em relação a um eixo
ou um giro em torno de um ponto fixo.

16. Duas retas paralelas

17. Duas retas paralelas e uma
transversal

18. Quantos ângulos temos aqui?
Isso mesmo, temos oito ângulos!

19. Qual a medida dos ângulos indicados?
Eles estão na mesma posição em relação à reta
transversal?
O que podemos afirmar em relação às suas medidas?
Concluímos que x = 40º.

20. Qual a medida dos ângulos indicados?
Eles estão na mesma posição em relação à reta
transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 5x – 40º = 3x
+ 20º, cujo resultado é x = 30º.

21. Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta
transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 2x + 10º = x +
30º, cujo resultado é x = 20º.