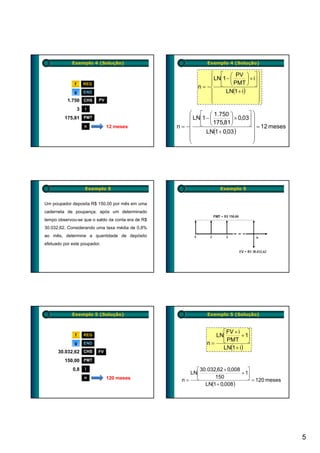
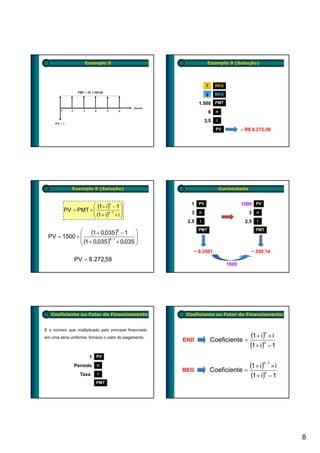
1) O documento apresenta exemplos de cálculos envolvendo séries uniformes, como financiamentos, aplicações e aposentadoria. 2) São mostrados conceitos como taxa de juros, valor presente, valor futuro, número de períodos e valor das prestações. 3) Os exemplos são resolvidos passo a passo utilizando fórmulas de séries uniformes para cálculo de valor presente, valor futuro e valor das prestações.

1. Séries Uniformes Financiamentos
Séries Uniformes são aquelas em que os Piroca financiou um carro no valor de
pagamentos ou recebimentos são constantes e R$ 30.000,00 em 60 parcelas sem entrada, a
ocorrem em intervalos iguais juros de 2,08% a.m. Quanto deverá pagar de
prestações?
t õ ?
Financiamentos Aposentadoria
Quanto eu tenho que depositar
mensalmente durante 30 anos
f REG
a juros de 1,5% a.m. para ter
30000 PV
R$ 1 000 000 00?
1.000.000,00?
60 n
2,08 i
PMT − R$ 879,84
1

2. Aposentadoria Aplicação de Séries Uniformes
Leasing
f REG
1.000.000 FV Crédito Financiamentos
Pessoal Imobiliários
360 n
1,5 i
PMT − R$ 70,85
Crediários CDC
Tipos de Séries Uniformes Tipos de Séries Uniformes
Séries Antecipadas = Begin = BEG Séries Postecipadas = END
g BEG g END
Exemplo 1 Exemplo 1
Um produto é comercializado a vista por R$ 500,00.
Qual deve ser o valor da prestação se o comprador
resolver financiar em cinco prestações mensais
iguais e sem entrada, considerando que a t
i i t d id d taxa d
de
juros cobrada seja de 5% a.m.?
2

3. Exemplo 1 (Solução) Exemplo 1 (Solução)
⎛ (1 + i)n × i ⎞
f REG PMT = PV × ⎜
⎜ (1 + i)n − 1⎟
⎟
g END
⎝ ⎠
500 CHS PV
⎛ (1 + 0,05 )5 × 0,05 ⎞
5 n PMT = 500 × ⎜
⎜ (1 + 0,05 )5 − 1 ⎟
⎟
5 i ⎝ ⎠
PMT R$ 115,49
PMT = 115,49
Exemplo 2 Exemplo 2
Qual é o valor de um financiamento a ser quitado
através de 6 pagamentos mensais de R$ 1.500,00,
vencendo a primeira parcela após 30 dias da
liberação dos recursos (sem entrada), sendo de
3,5% a.m. a taxa de juros negociada na operação?
Exemplo 2 (Solução) Exemplo 2 (Solução)
⎛ (1 + i)n − 1⎞
f REG PV = PMT × ⎜ ⎟
⎜ (1 + i)n × i ⎟
g END ⎝ ⎠
1.500
1 500 PMT
⎛ (1 + 0,035 )6 − 1 ⎞
6 n
PV = 1500 × ⎜ ⎟
⎜ (1 + 0,035 )6 × 0,035 ⎟
3,5 i ⎝ ⎠
PV – R$ 7.992,83
PV = 7.992,83
3

4. Exemplo 3 Exemplo 3
Determinar o valor dos depósitos mensais que,
quando aplicado a uma taxa de 4% ao mês durante
7 meses, produz um montante de R$ 5.000,00,
pelo regime de juros compostos.
Exemplo 3 (Solução) Exemplo 3 (Solução)
⎛ i ⎞
f REG PMT = FV × ⎜ ⎟
⎜ (1 + i)n − 1 ⎟
g END ⎝ ⎠
5.000
5 000 CHS FV
7 n ⎛ 0,04 ⎞
PMT = 5000 × ⎜ ⎟
⎜ (1 + 0,04 )7 − 1⎟
4 i ⎝ ⎠
PMT R$ 633,05
PMT = 633,05
Exemplo 4 Exemplo 4
Um produto é comercializado a vista por R$
1.750,00. Uma outra alternativa seria financiar
este produto a uma taxa de 3% ao mês, gerando
uma prestação de R$ 175,81; considerando que o
comprador escolha a segunda alternativa,
determinar a quantidade de prestações deste
financiamento (sem entrada)
4

5. Exemplo 4 (Solução) Exemplo 4 (Solução)
⎧ ⎡ ⎛ PV ⎞ ⎤ ⎫
⎪ LN⎢1 − ⎜ ⎟ × i⎥ ⎪
f REG ⎪ ⎣ ⎝ PMT ⎠ ⎦ ⎪
n = −⎨ ⎬
g END ⎪ LN(1 + i) ⎪
1.750
1 750 CHS PV ⎪
⎩ ⎪
⎭
3 i
⎛ ⎡ ⎛ 1.750 ⎞ ⎤⎞
175,81 PMT ⎜ LN⎢1 − ⎜ ⎟ × 0,03⎥ ⎟
⎜ ⎝ 175,81 ⎠ ⎦ ⎟ = 12 meses
n 12 meses n = −⎜ ⎣ ⎟
⎜ LN(1 + 0,03 ) ⎟
⎜ ⎟
⎝ ⎠
Exemplo 5 Exemplo 5
Um poupador deposita R$ 150,00 por mês em uma
caderneta de poupança; após um determinado
tempo observou-se que o saldo da conta era de R$
30.032,62. Considerando uma t
30 032 62 C id d taxa média d 0 8%
édi de 0,8%
ao mês, determine a quantidade de depósito
efetuado por este poupador.
Exemplo 5 (Solução) Exemplo 5 (Solução)
⎡ FV × i ⎤
f REG LN⎢ + 1⎥
g END n= ⎣ PMT ⎦
LN(1 + i)
30.032,62
30 032 62 CHS FV
150,00 PMT
0,8 i ⎡ 30.032,62 × 0,008 ⎤
LN⎢ + 1⎥
n 120 meses n= ⎣ 150 ⎦ = 120 meses
LN(1 + 0,008 )
5

6. Exemplo 6 Exemplo 6
Um automóvel é comercializado por R$ 17.800,00 à
vista; sabendo-se que pode ser financiado em 36
parcelas mensais (sem entrada) de R$ 1.075,73,
determinar a taxa de juros da operação.
Exemplo 6 (Exemplo) Exemplo 7
f REG Uma pessoa realiza depósitos mensais no valor de
g END R$ 100,00 em uma caderneta de poupança;
considerando uma taxa de 0,8% ao mês, e um
17.800
17 800 CHS PV
prazo de trinta anos, qual será o valor acumulado
1.075,73 PMT
após este período?
36 n
i 5% a.m.
Exemplo 7 Exemplo 7 (Solução)
f REG
g END
100 PMT
0,8 i
360 n
FV – R$ 207.641,32
6

7. Exemplo 7 (Solução) Exemplo 8
⎡ (1 + i)n − 1⎤ Um produto é comercializado a vista por R$
FV = PMT × ⎢ ⎥
i 500,00. Qual deve ser o valor da prestação se o
⎣ ⎦
comprador resolver financiar em cinco prestações
⎡ (1 + 0,008 )360 − 1⎤ mensais iguais e com entrada, considerando que
FV = 100 × ⎢ ⎥ a taxa de juros cobrada seja de 5% a.m.?
⎣ 0,008 ⎦
FV = 207.641,32
Exemplo 8 Exemplo 8 (Solução)
f REG
g BEG
500 CHS PV
5 n
5 i
PMT R$ 109,99
Exemplo 8 (Solução) Exemplo 9
⎛ (1 + i)n−1 × i ⎞ Qual é o valor de um financiamento a ser quitado
PMT = PV × ⎜
⎜ (1 + i)n − 1 ⎟
⎟
⎝ ⎠ através de 6 pagamentos mensais de R$ 1.500,00,
vencendo a primeira parcela no ato da liberação
⎛ (1 + 0,05 )5−1 × 0,05 ⎞ dos recursos (com entrada), sendo de 3,5% a.m. a
PMT = 500 × ⎜
⎜ (1 + 0,05 )5 − 1 ⎟
⎟ taxa de juros negociada na operação?
⎝ ⎠
PMT = 109,99
7

8. Exemplo 9 Exemplo 9 (Solução)
f REG
g BEG
1.500 PMT
6 n
3,5 i
PV – R$ 8.272,58
Exemplo 9 (Solução) Curiosidade
⎛ (1 + i)n − 1 ⎞ 1 PV 1000 PV
PV = PMT × ⎜ ⎟
⎜ (1 + i)n−1 × i ⎟ 3 n 3 n
⎝ ⎠
2,5 i 2,5 i
⎛ (1 + 0,035 )6 − 1 ⎞ PMT PMT
PV = 1500 × ⎜ ⎟
⎜ (1 + 0,035 )6−1 × 0,035 ⎟
⎝ ⎠
− 0,3501 − 350,14
PV = 8.272,58
1000
Coeficiente ou Fator de Financiamento Coeficiente ou Fator de Financiamento
É o número que multiplicado pelo principal financiado
em uma série uniforme, fornece o valor do pagamento.
END Coeficiente =
(1 + i)n × i
(1 + i)n − 1
1 PV
Período n
BEG Coeficiente =
(1 + i)n−1 × i
Taxa i
(1 + i)n − 1
PMT
8