O documento explica o conceito de juros compostos, onde os juros de cada período são calculados sobre o montante acumulado anterior. Apresenta a fórmula matemática para calcular juros compostos e exemplos numéricos ilustrando o cálculo do montante, valor dos juros, taxa e períodos de capitalização.

1. Juros Compostos Juros Compostos
No regime de capitalização composta o valor dos No Brasil os juros compostos são conhecidos
juros para o período atual é obtido pela aplicação da popularmente como “juros sobre juros”
taxa de juros sobre o montante acumulado até o início
desse período
Juros Compostos Juros Compostos
No Brasil, a maioria das operações do mercado Podemos calcular juros compostos fazendo uma
financeiro é calculada a juros compostos, por sucessão de cálculos de juros simples, calculando o
exemplo: Certificados de Depósitos Bancários, Fundos montante para cada período de capitalização, utilizando
de Investimento, Caderneta de Poupança, sempre como base de cálculo o valor futuro ou o
Financiamentos H bit i
Fi i t Habitacionais, C diá i
i Crediários, L
Leasing etc.
i t montante conseguido no período d capitalização
t t id í d de it li ã
anterior.
1

2. Juros Compostos Juros Compostos
A fórmula de juros simples para cada período de Valor futuro após o primeiro período de capitalização:
capitalização (cada dia, cada mês etc.) é a seguinte:
FV1 = PV × (1 + i)
FV = PV × (1 + i) Valor futuro após o segundo período de capitalização:
FV2 = FV1 × (1 + i)
Nota: a variável “n” será desprezada pois será sempre 1
FV2 = PV × (1 + i) × (1 + i)
Juros Compostos Juros Compostos
Valor futuro após o terceiro período de capitalização:
FV3 = FV2 × (1 + i)
FV = PV (1 + i)n
FV3 = PV × (1 + i) × (1 + i) × (1 + i)
FV = Valor Futuro (Future Value)
Valor futuro após “n” períodos de capitalização:
PV = Valor Presente (Present Value)
i = Taxa (Interest Rate)
FVn = PV × (1 + i)n n = Período (Number of periods)
Exemplo 1 (Método Algébrico) Exemplo 1 (HP-12C)
Uma pessoa aplicou o valor de R$ 600,00 à taxa de Uma pessoa aplicou o valor de R$ 600,00 à taxa de
2% a.m. durante 5 meses. Calcule o montante. 2% a.m. durante 5 meses. Calcule o montante.
f FIN
600 PV
2 i
5 n
FV – 662,45
2

3. Cálculo do Juros Cálculo do Juros
Para calcular apenas o valor dos juros, partimos da
n
idéia de que: INT = PV × (1 + i) – PV
FV = PV + INT
E, deixando o PV em evidência, teremos:
Daí pode-se dizer que:
INT = PV × [(1 + i)n – 1]
INT = FV – PV
E, finalmente:
INT = PV × (1 + i)n – PV
Exemplo 2 (Método Algébrico) Derivações da Fórmula
Uma pessoa aplicou o valor de R$ 600,00 à taxa de
2% a.m. durante 5 meses. Calcule o valor dos juros.
.
n
FV PV 1 i .
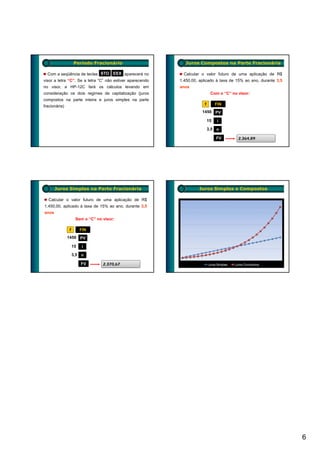
Exemplo 3 (Método Algébrico) Exemplo 3 (HP-12C)
Calcule o montante para um principal de R$ 1.470,00 Calcule o montante para um principal de R$ 1.470,00
a uma taxa de 2,00% a.m. num prazo de 5 meses a uma taxa de 2,00% a.m. num prazo de 5 meses
f FIN
1470 PV
2 i
5 n
FV – 1.623,00
3

4. Exemplo 4 (Método Algébrico) Exemplo 4 (HP-12C)
Calcule o principal que gerou um montante de Calcule o principal que gerou um montante de
R$ 1.623,00 a uma taxa de 2,00% a.m. num prazo de 5 R$ 1.623,00 a uma taxa de 2,00% a.m. num prazo de 5
meses. meses.
f FIN
1623 FV
2 i
5 n
PV – 1.470,00
Exemplo 5 (Método Algébrico) Exemplo 5 (HP-12C)
Calcule a taxa mensal para um principal de Calcule a taxa mensal para um principal de
R$ 1.470,00 que gerou um montante de R$ 1.623,00 R$ 1.470,00 que gerou um montante de R$ 1.623,00
num prazo de 5 meses. num prazo de 5 meses.
f FIN
1470 PV
1623 CHS FV
5 n
i 2%
Exemplo 6 (Método Algébrico) Exemplo 6 (HP-12C)
Calcule o número de períodos de capitalização para Calcule o número de períodos de capitalização para
um principal de R$ 1.470,00, montante de um principal de R$ 1.470,00, montante de
R$ 1.623,00 à taxa de 2,00% a.m. R$ 1.623,00 à taxa de 2,00% a.m.
f FIN
1470 PV
1623 CHS FV
2 i
n 5 meses
4

5. Exemplo 7 (Método Algébrico) Exemplo 7 (HP-12C)
Calcule o número de períodos de capitalização para Calcule o número de períodos de capitalização para
um principal de R$ 1.000,00, montante de um principal de R$ 1.000,00, montante de
R$ 1.211,83 à taxa de 3,00% a.m. R$ 1.211,83 à taxa de 3,00% a.m.
f FIN
1211,83 PV
1000 CHS FV
3 i
n 7 meses
Curiosidade Curiosidade
Observe que os resultados encontrados pela fórmula A HP-12C arredonda a resposta n para o inteiro
e pela HP-12C são diferentes, e fica evidente que a imediatamente superior nos casos em que o resultado
resposta encontrada pela HP-12C não está correta for fracionário. No exemplo anterior, o resultado correto
é de 6,5 meses; assim, a HP-12C arredondou o
resultado para 7
Curiosidade Período Fracionário
Para contornar esse problema de arredondamento na Quando o tempo de uma aplicação não for um número
HP-12C, deve-se armazenar no registrador financeiro inteiro, podemos ter três possibilidades:
i a taxa equivalente diária a juros compostos para
que o resultado do prazo seja calculado e fornecido em Somente ter remuneração pelo número inteiro de
uma quantidade exata de dias. períodos de capitalização, como ocorre com a
caderneta de poupança
Os juros do número inteiro de períodos de
capitalização são calculados a juros compostos e a
parte fracionária a juros simples
São calculados juros compostos pelo tempo todo,
inclusive na parte fracionária
5

6. Período Fracionário Juros Compostos na Parte Fracionária
Com a seqüência de teclas STO EEX aparecerá no Calcular o valor futuro de uma aplicação de R$
visor a letra “C”. Se a letra “C” não estiver aparecendo 1.450,00, aplicado à taxa de 15% ao ano, durante 3,5
no visor, a HP-12C fará os cálculos levando em anos
consideração os dois regimes de capitalização (juros Com o “C” no visor:
compostos na parte inteira e juros simples na parte
fracionária) f FIN
1450 PV
15 i
3,5 n
FV 2.364,89
Juros Simples na Parte Fracionária Juros Simples e Compostos
Calcular o valor futuro de uma aplicação de R$
1.450,00, aplicado à taxa de 15% ao ano, durante 3,5
anos
Sem o “C” no visor:
f FIN
1450 PV
15 i
3,5 n
FV 2.370,67
6