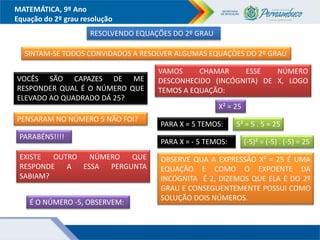
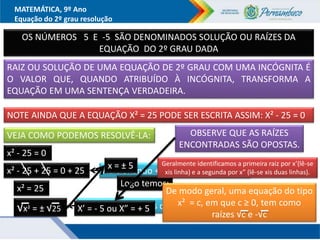
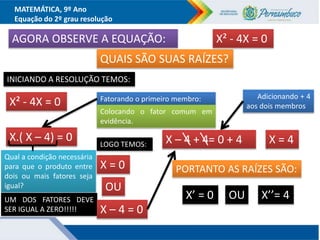
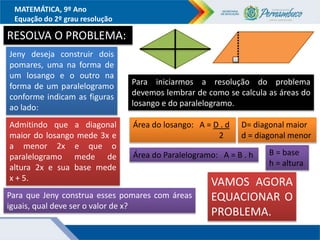
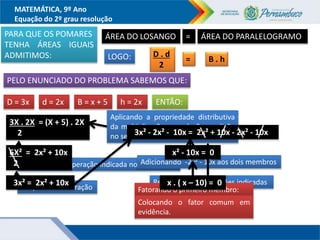
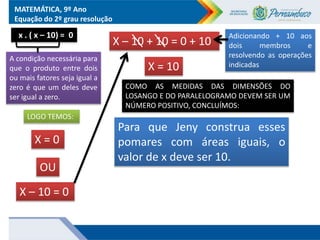
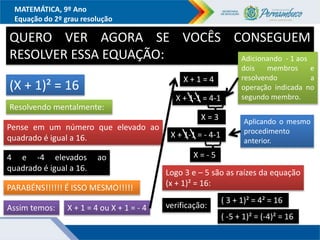
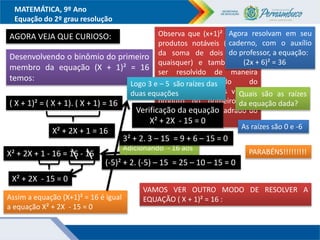
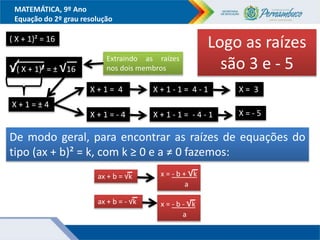
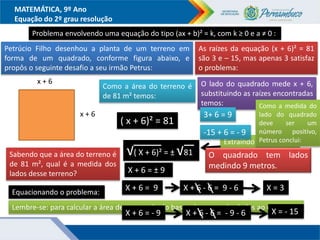
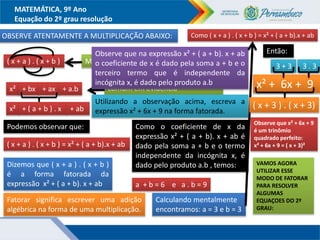
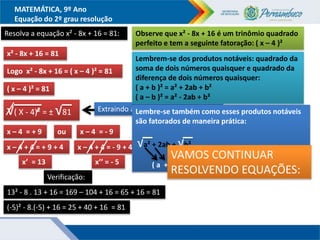
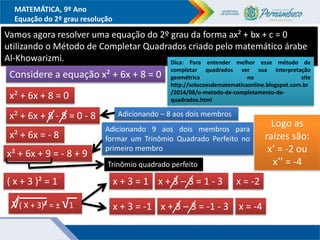
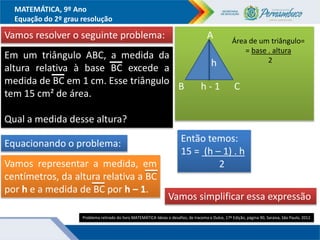
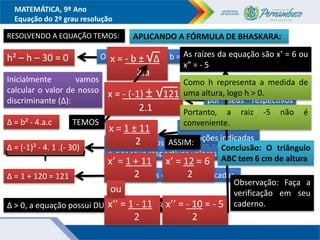
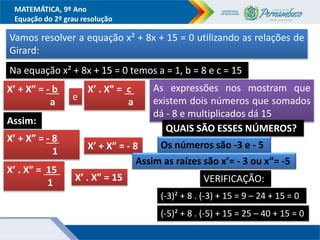
O documento discute métodos para resolver equações do segundo grau, incluindo fatoração, completar quadrados e a fórmula de Bhaskara. Recomenda-se ensinar esses métodos além da fórmula para que os alunos entendam melhor o significado da fórmula. Exemplos ilustram como aplicar os métodos para encontrar as raízes das equações.