Baixado 18 vezes
Carregado porRosana Santos Quirino
Solidos cilindro
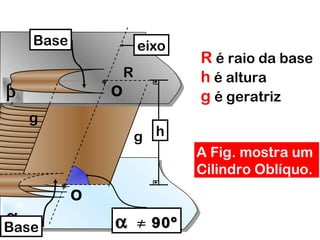
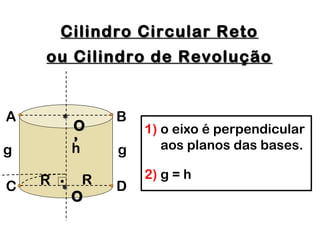
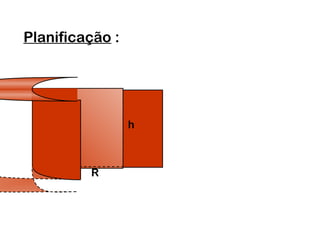
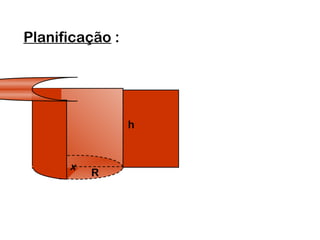
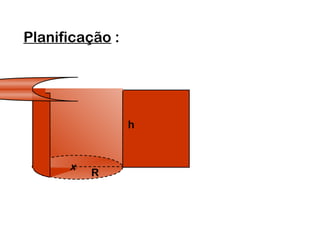
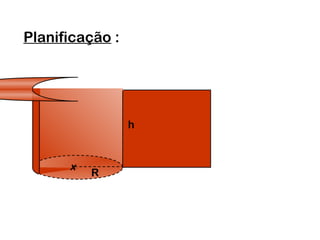
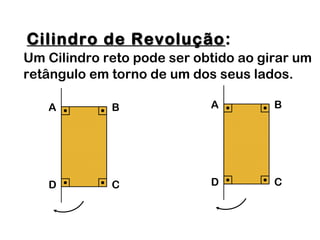
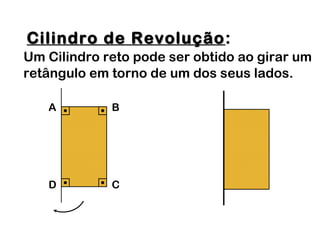
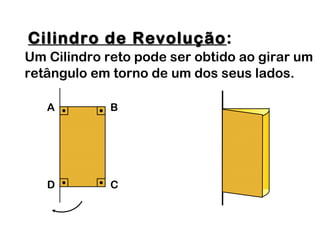
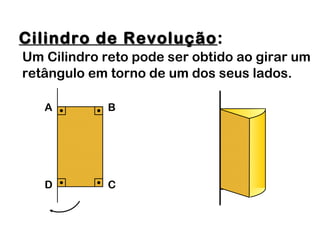
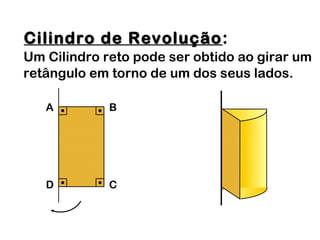
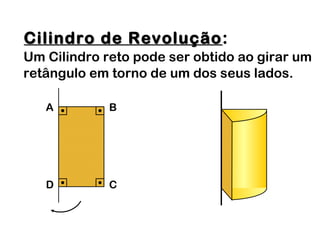
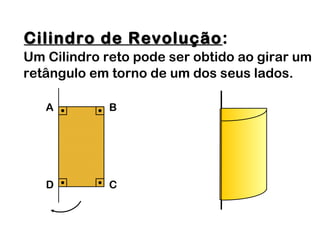
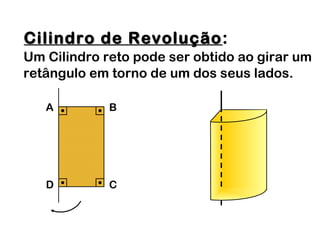
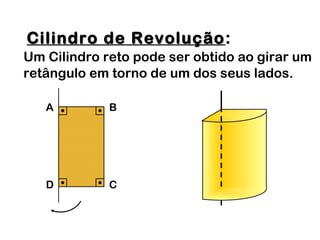
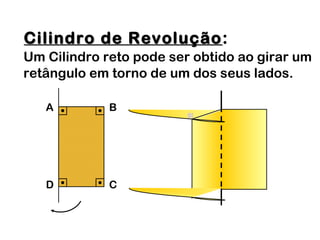
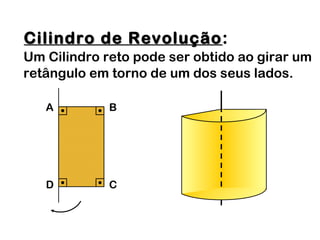
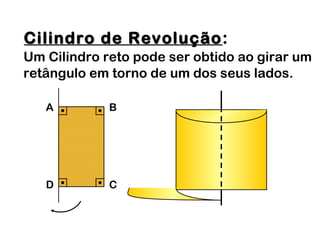
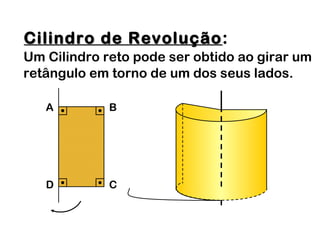
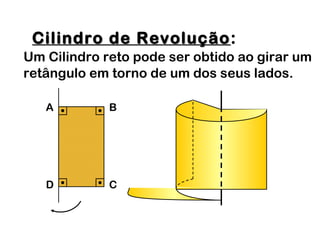
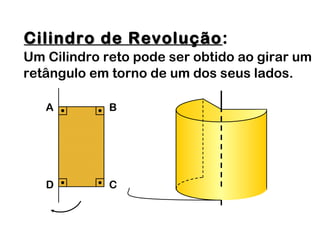
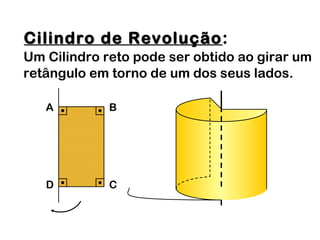
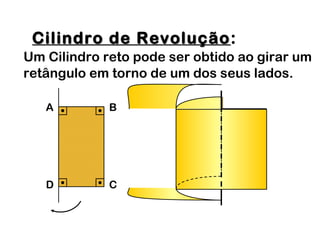
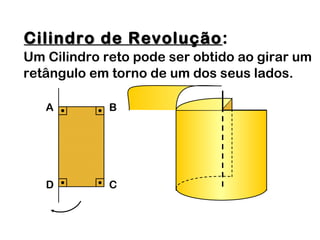
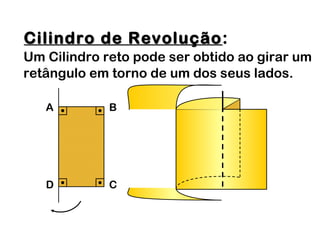
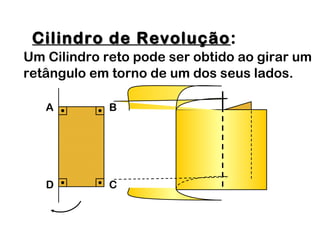
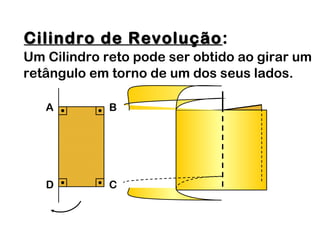
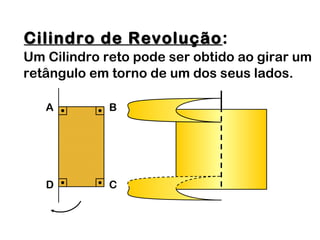
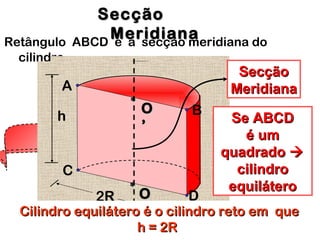
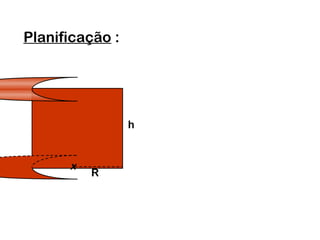
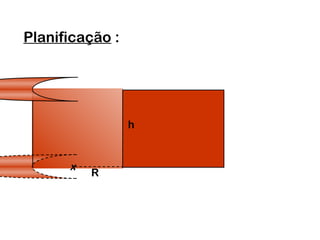
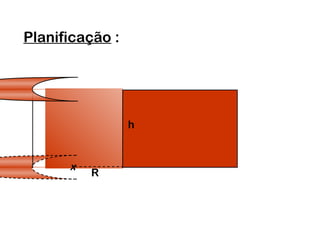
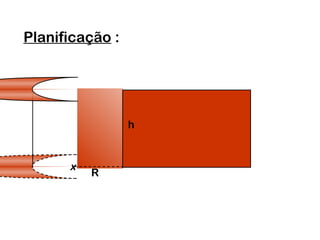
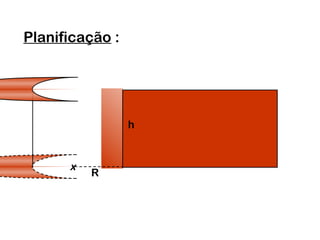
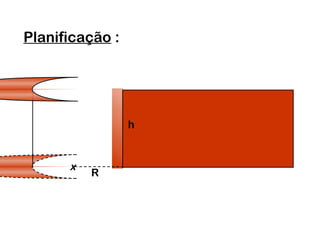
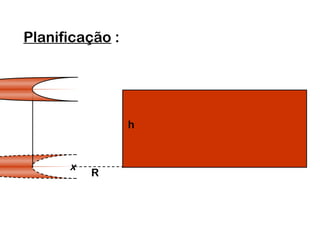
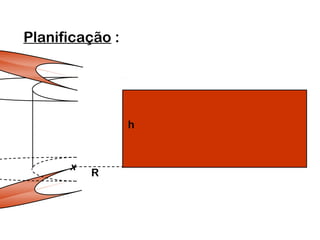
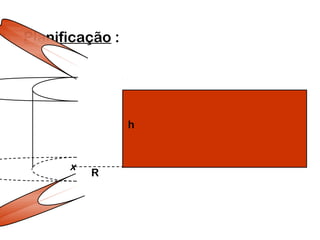
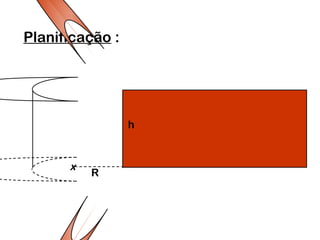
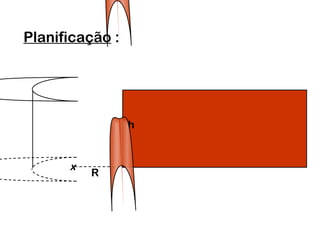
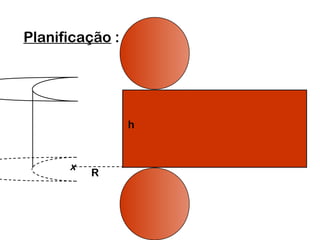
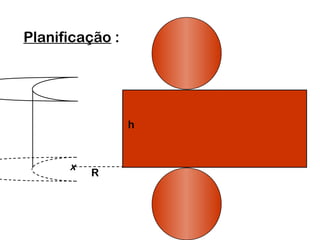
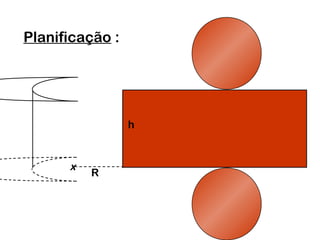
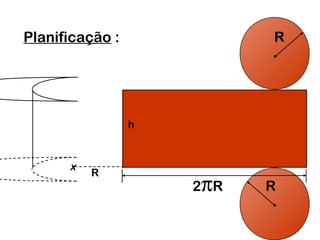
1) O documento discute os tipos de cilindros geométricos, incluindo cilindros oblíquos, retos e de revolução. 2) Um cilindro reto pode ser formado girando um retângulo em torno de um de seus lados. 3) O documento fornece fórmulas para calcular a área lateral, área total e volume de um cilindro.
Solidos cilindro
- 1. Disciplina: Matemática Tema: SólidosGeométricos - Cilindros Professora:ROSANA QUIRINO
- 2. αα g g ββββ eixo αα 90º90ºBase Base O** O** R h A Fig.mostra um Cilindro Oblíquo. R é raio da base h é altura g é geratriz
- 3. Cilindro Circular RetoCilindroCircular Reto OO** g gh 1) o eixo é perpendicular aos planos das bases. R DC ou Cilindro de Revoluçãoou Cilindro de Revolução R BA OO ’’ ** 2) g = h
- 4. A B D C AB D C Cilindro de RevoluçãoCilindro de Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados.
- 5. A B D C Cilindrode RevoluçãoCilindro de Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados.
- 6. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 7. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 8. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 9. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 10. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 11. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 12. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 13. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 14. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 15. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 16. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 17. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 18. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 19. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 20. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 21. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 22. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 23. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 24. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 25. Cilindro de RevoluçãoCilindrode Revolução: Um Cilindro reto pode ser obtido ao girar um retângulo em torno de um dos seus lados. A B D C
- 26. Retângulo ABCD éa secção meridiana do cilindro. 2R SecçãoSecção MeridianaMeridianaA B C DOO** OO ’’ ** h Se ABCDSe ABCD é umé um quadradoquadrado cilindrocilindro equiláteroequilátero Cilindro equilátero é o cilindro reto em queCilindro equilátero é o cilindro reto em que h = 2Rh = 2R SecçãoSecção MeridianaMeridiana
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48. Áreas e VolumesÁrease Volumes AALL = 2= 2ππ RhRhAALL = 2= 2ππ RhRh At = AL+ 2 Ab V = ππ RR22 . h Área Lateral ( AL ) Área Total ( At ) Volume ( V) AAbb == ππ RR22 AAbb == ππ RR22Área Base ( Ab )