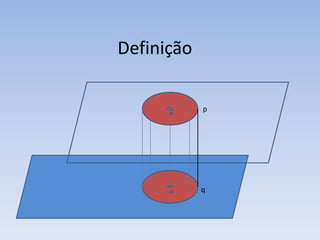
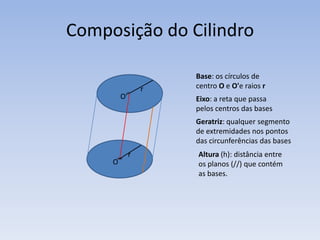
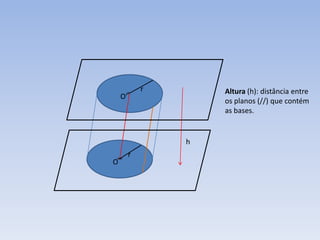
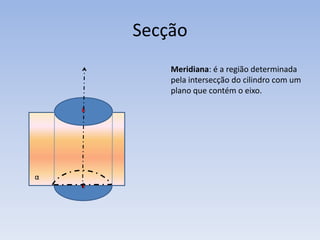
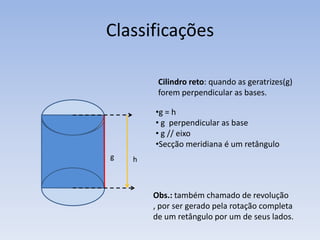
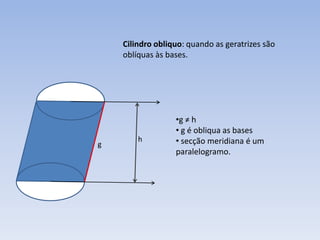
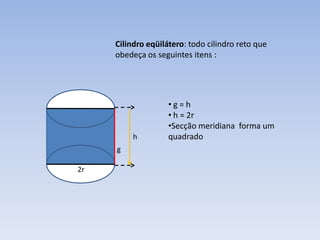
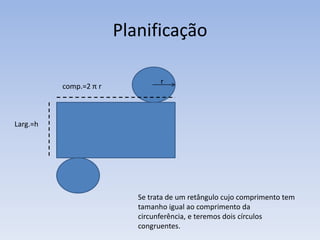
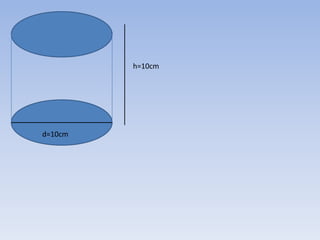
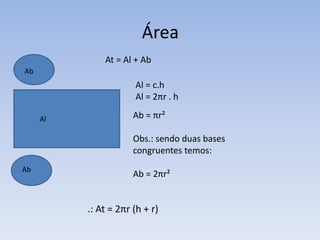
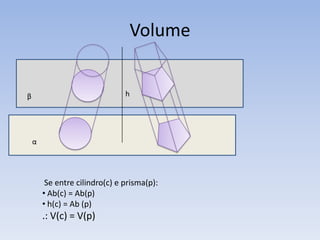
1) O documento descreve as características geométricas de um cilindro, incluindo sua composição, classificações, planificação, área e volume. 2) Um cilindro é formado por duas bases circulares paralelas conectadas por geratrizes retas paralelas ao eixo. Sua altura é a distância entre os planos das bases. 3) O documento fornece fórmulas para calcular a área total e o volume de um cilindro.

1. CILINDROS
Acadêmicos :Camila Campos Carvalho
II Período (Licenciatura Matemática)
Geometria II

2. Definição
p
q

3. Composição do Cilindro
Base: os círculos de
r centro O e O'e raios r
O’ Eixo: a reta que passa
pelos centros das bases
Geratriz: qualquer segmento
de extremidades nos pontos
das circunferências das bases
r Altura (h): distância entre
O os planos (//) que contém
as bases.

4. r Altura (h): distância entre
O’
os planos (//) que contém
as bases.
h
r
O

5. Secção
Meridiana: é a região determinada
pela intersecção do cilindro com um
plano que contém o eixo.
α

6. Classificações
Cilindro reto: quando as geratrizes(g)
forem perpendicular as bases.
•g = h
• g perpendicular as base
• g // eixo
•Secção meridiana é um retângulo
g h
Obs.: também chamado de revolução
, por ser gerado pela rotação completa
de um retângulo por um de seus lados.

7. Cilindro de revolução

8. Cilindro obliquo: quando as geratrizes são
oblíquas às bases.
•g ≠ h
• g é obliqua as bases
g
h • secção meridiana é um
paralelogramo.

9. Cilindro eqüilátero: todo cilindro reto que
obedeça os seguintes itens :
•g=h
• h = 2r
•Secção meridiana forma um
h quadrado
g
2r

10. Planificação
r
comp.=2 π r
Larg.=h
Se trata de um retângulo cujo comprimento tem
tamanho igual ao comprimento da
circunferência, e teremos dois círculos
congruentes.

11. Área
At = Al + Ab
Ab
Al = c.h
Al = 2πr . h
Al Ab = πr²
Obs.: sendo duas bases
congruentes temos:
Ab
Ab = 2πr²
.: At = 2πr (h + r)

12. Volume
β h
α
Se entre cilindro(c) e prisma(p):
• Ab(c) = Ab(p)
• h(c) = Ab (p)
.: V(c) = V(p)

13. Volume
V = Ab . h
Se Ab = πr²
h
.: V = πr² . h
r

14. Exercícios
1. Um tanque, na forma de um cilindro regular
com 10cm de altura e de diâmetro (medidas
externas), tampado superiormente, é usado
como deposito de óleo combustível.
Anualmente, é feita uma pintura de sua
superfície externa (excluindo-se a pintura da
base inferior).Sabe-se que, com uma lata de
tinta, pintam-se 26m² da superfície.
Considerando π=3,14, para se pintar todo o
tanque são necessários, aproximadamente:

15. h=10cm
d=10cm

16. a) 7 latas
b) 15 latas
c) 18 latas
d) 20 latas
e) 21 latas

17. 2. Para medir o volume de uma pedra
irregular,um estudante utilizou um copo de
forma cilíndrica, de diâmetro 6cm, com água
até certa altura. Marcou o nível da água em
repouso, deixou a pedra mergulhar e marcou
o novo nível. Considerando π=3,14, se o
desnível observado foi de 2cm, então o
volume da pedra é:

18. a) 56,52cm³
b) 226,08cm³
c) 18,84cm³
d) 80cm³
e) 160cm³