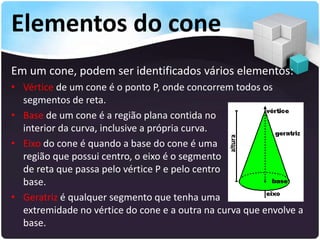
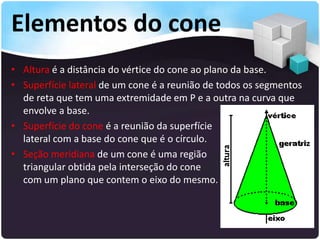
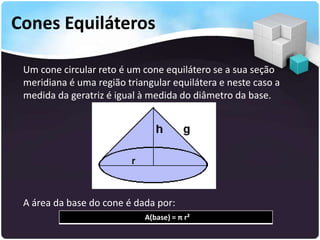
O documento descreve os principais elementos de um cone, incluindo vértice, base, eixo, geratriz, altura, superfícies lateral e total. Explica que os cones podem ser classificados como retos ou oblíquos dependendo da posição do eixo em relação à base. Também fornece fórmulas para calcular áreas laterais e totais de cones circulares retos.

1. GEOMETRIA MÉTRICA ESPACIAL
CONE

2. Conceito
Considere uma região plana limitada por uma curva suave
(sem quinas), fechada e um ponto P fora desse plano.
Denominamos cone ao sólido formado pela reunião de todos os
segmentos de reta que têm uma extremidade em um ponto P
(vértice) e a outra num ponto qualquer da região.

3. Elementos do cone
Em um cone, podem ser identificados vários elementos:
• Vértice de um cone é o ponto P, onde concorrem todos os
segmentos de reta.
• Base de um cone é a região plana contida no
interior da curva, inclusive a própria curva.
• Eixo do cone é quando a base do cone é uma
região que possui centro, o eixo é o segmento
de reta que passa pelo vértice P e pelo centro da
base.
• Geratriz é qualquer segmento que tenha uma
extremidade no vértice do cone e a outra na curva que envolve a
base.

4. Elementos do cone
• Altura é a distância do vértice do cone ao plano da base.
• Superfície lateral de um cone é a reunião de todos os segmentos
de reta que tem uma extremidade em P e a outra na curva que
envolve a base.
• Superfície do cone é a reunião da superfície
lateral com a base do cone que é o círculo.
• Seção meridiana de um cone é uma região
triangular obtida pela interseção do cone
com um plano que contem o eixo do mesmo.

5. Classificação do cone
Ao observar a posição relativa do eixo em relação à base, os
cones podem ser classificados como retos ou oblíquos. Um cone é
dito reto quando o eixo é perpendicular ao plano da base e é
oblíquo quando não é um cone reto. Ao lado apresentamos um
cone oblíquo.
Observação: Para efeito de aplicações, os cones mais
importantes são os cones retos. Em função das bases,
os cones recebem nomes especiais. Por exemplo:
um cone é dito circular se a base é um círculo e é dito
elíptico se a base é uma região elíptica.

6. Observações sobre um cone circular reto
Um cone circular reto é denominado cone de revolução por ser
obtido pela rotação (revolução) de um triângulo retângulo em
torno de um de seus catetos
A seção meridiana do cone circular reto é a interseção do cone com um plano
que contem o eixo do cone. Na figura ao lado, a seção meridiana é a região
triangular limitada pelo triângulo isósceles VAB.

7. Cones
Em um cone circular reto, todas as geratrizes são congruentes
entre si. Se g é a medida da geratriz então, pelo Teorema de
Pitágoras, temos uma relação notável no cone: g²=h²+r², que
pode ser "vista" na figura abaixo:

8. Áreas
A Área Lateral de um cone circular reto pode ser obtida em
função de g (medida da geratriz) e r (raio da base do cone):
Área total de um cone circular reto pode ser obtida em função de
g (medida da geratriz) e r (raio da base do cone):
A(lateral) = π.r.g
A(total) = π.r.g + π.r² = π.r.(g+r)

9. Cones Equiláteros
Um cone circular reto é um cone equilátero se a sua seção
meridiana é uma região triangular equilátera e neste caso a
medida da geratriz é igual à medida do diâmetro da base.
A área da base do cone é dada por:
A(base) = π r²

10. Cones Equiláteros
Pelo Teorema de Pitágoras temos que (2r)²=h²+r², logo
h²=4r²-r²=3r², assim
Como o volume do cone é obtido por 1/3 do produto da
área da base pela altura, então:
Como a área lateral pode ser obtida por:
Então a área total será dada por:
h = r
V = (1/3) π r3
A(lateral) =π.r.g = π.r.2r = 2. π.r²
A(total) = 3 π r²

11. ANEXOS

12. ANEXOS

13. Exercícios Resolvidos
Um cone possui diâmetro da base medindo 24 cm, geratriz 20 cm
e altura igual a 16 cm. Determine sua área total e seu volume.
Área total Volume
A = π * r * (g + r)
A = 3,14 * 12 * (20 + 12)
A = 3,14 * 12 * 32
A = 1 205,76 cm²

14. Exercícios Resolvidos
Um cone possui raio da base medindo 4 cm e altura igual a 10 cm.
Determine a altura de um líquido que ocupa nesse cone o volume
de 100 cm³.

15. Exercícios Resolvidos
No cone reto a seguir, a geratriz (g) mede 20 cm e a altura mede
16 cm. Determine seu volume.
Resposta
Precisamos calcular a medida do raio
da base, e para isso utilizaremos o
teorema de Pitágoras. Observe

16. Exercícios Resolvidos
(Fuvest – SP) Um cone circular reto está Resposta
inscrito em um paralelepípedo reto retângulo,
de base quadrada, como mostra a figura.
A razão b a entre as dimensões do paralelepípedo
é 3/2 e o volume do cone é π. Determine o
comprimento g da geratriz do cone.

17. EQUIPE
• ANTONIO TÁLYSON DO NASCIMENTO
• BÁRBARA JAMYLLE MARTINS PIRES DE OLIVEIRA
• DOUGLAS ROGERIO FREITAS DE SOUZA
• MAURÍLIO FERNANDO CORREIA DA SILVA
• Prof°: Edinaldo
• EAPC – 2° ano EM - 2013