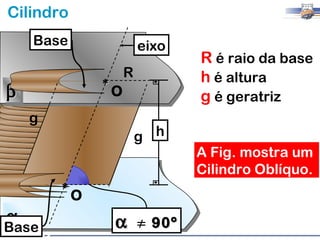
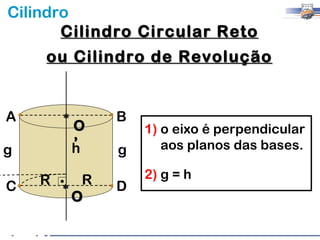
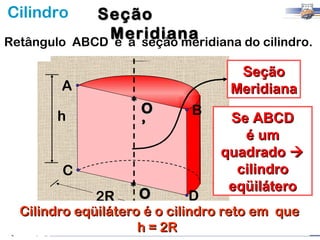
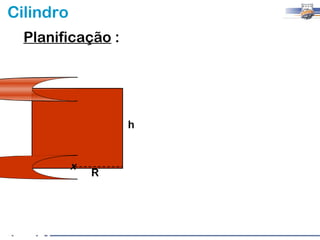
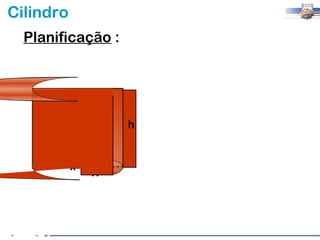
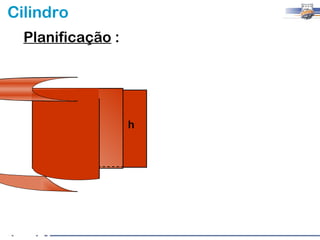
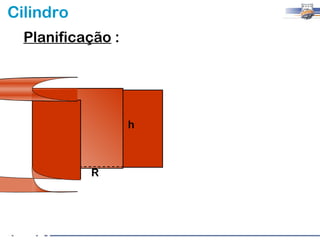
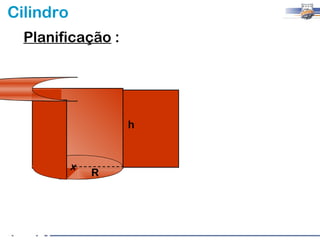
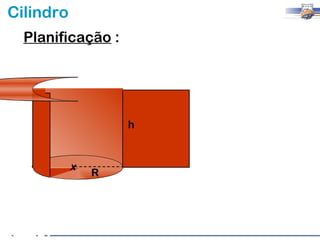
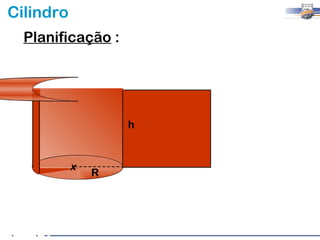
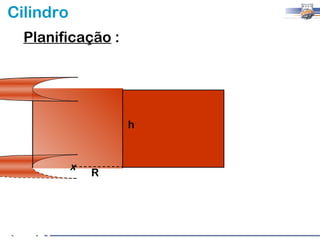
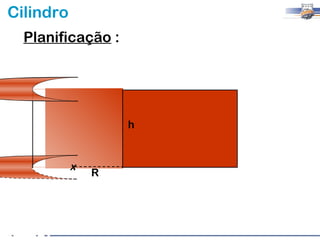
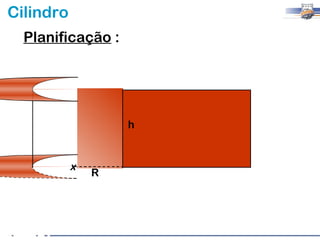
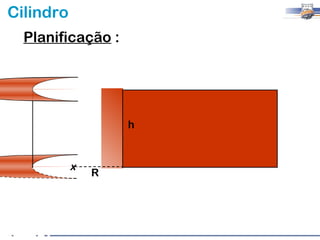
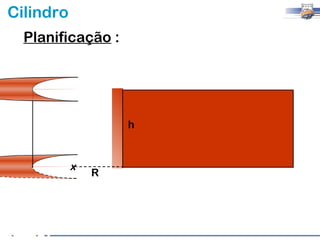
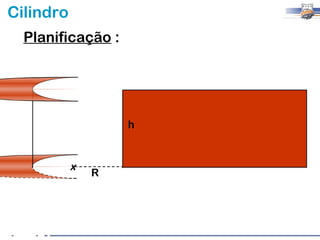
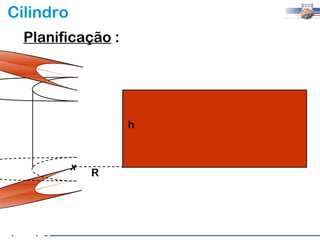
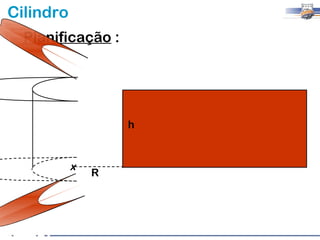
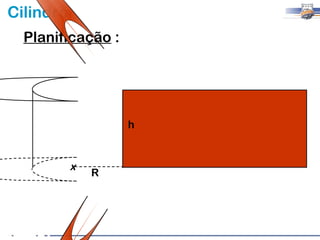
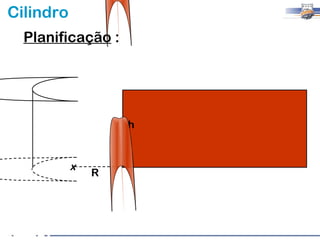
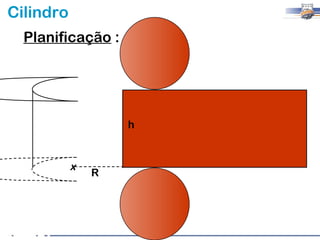
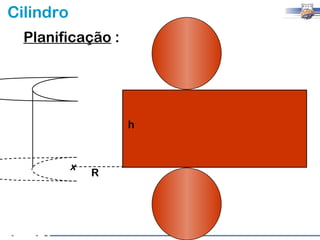
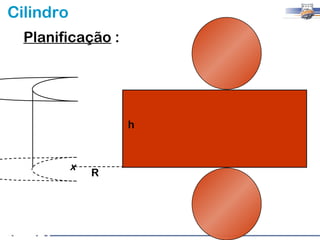
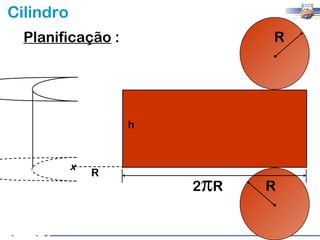
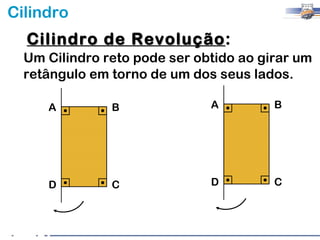
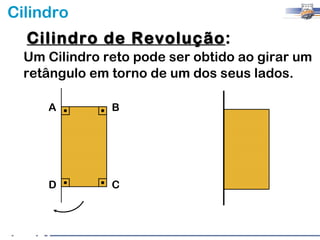
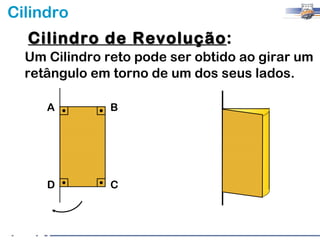
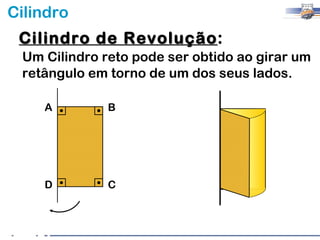
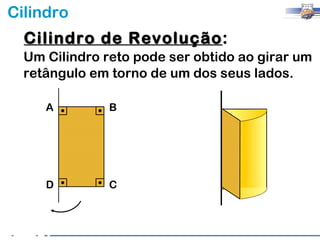
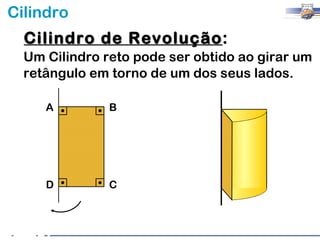
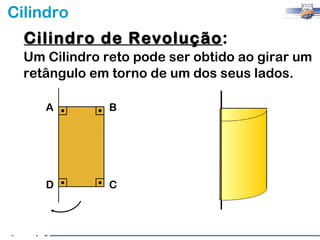
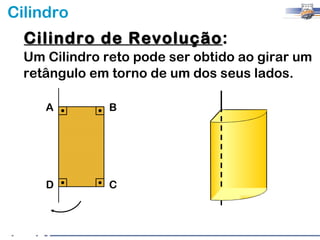
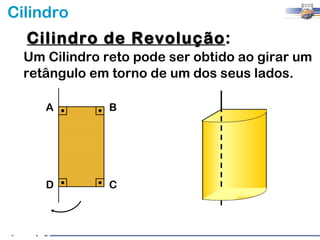
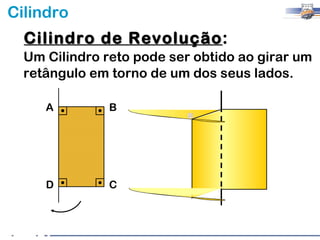
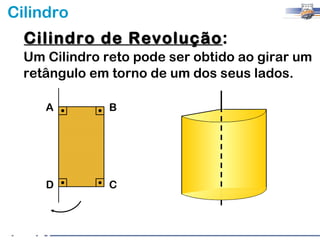
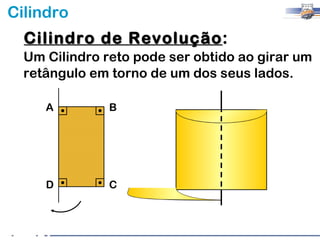
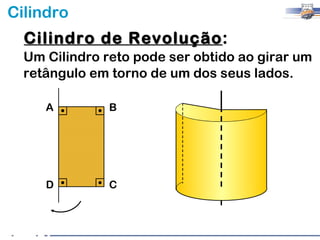
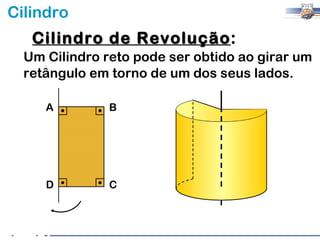
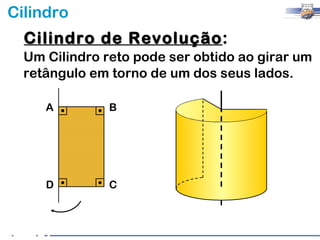
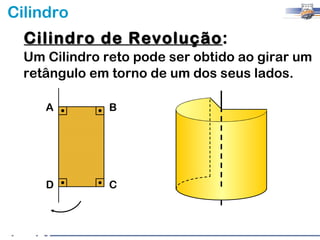
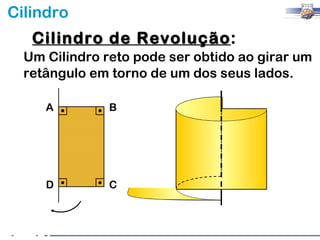
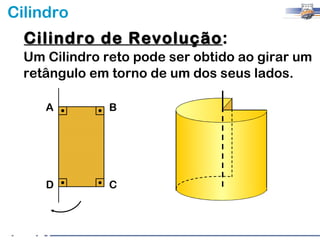
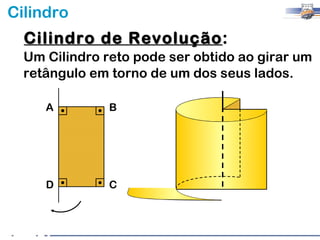
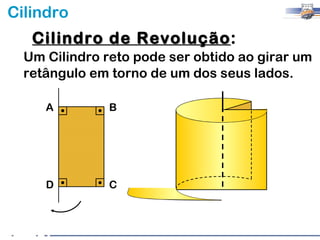
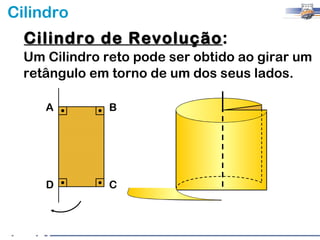
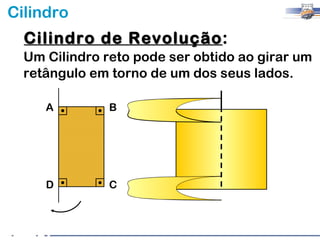
1) O documento descreve as características geométricas de um cilindro, incluindo sua base circular, altura e geratriz. 2) Um cilindro reto pode ser formado girando um retângulo em torno de um de seus lados. 3) As fórmulas para calcular a área total, área lateral e volume de um cilindro são apresentadas.

1. Cilindro
Segmento: Ensino Médio
Disciplina: Matemática
Tema: Sólidos Geométricos - Cilindros

2. Cilindro
Base eixo
R é raio da base
R h é altura
β *O
g é geratriz
g
g h
A Fig. mostra um
Cilindro Oblíquo.
*O
α α 90º
Base

3. Cilindro
Cilindro Circular Reto
ou Cilindro de Revolução
A *O B
1) o eixo é perpendicular
g ’
h g aos planos das bases.
R R 2) g = h
C *O D

4. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B A B
D C D C

5. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

6. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

7. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

8. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

9. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

10. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

11. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

12. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

13. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

14. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

15. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

16. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

17. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

18. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

19. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

20. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

21. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

22. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

23. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

24. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

25. Cilindro
Cilindro de Revolução:
Revolução
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A B
D C

26. Cilindro Seção
Retângulo
Meridiana
ABCD é a seção meridiana do cilindro.
Seção
A Meridiana
*O B
h Se ABCD
’
é um
quadrado 
C cilindro
2R *O D
eqüilátero
Cilindro eqüilátero é o cilindro reto em que
h = 2R

27. Cilindro
Planificação :
h
x
R

28. Cilindro
Planificação :
h
x
R

29. Cilindro
Planificação :
h
x
R

30. Cilindro
Planificação :
h
x
R

31. Cilindro
Planificação :
h
x
R

32. Cilindro
Planificação :
h
x
R

33. Cilindro
Planificação :
h
x
R

34. Cilindro
Planificação :
h
x
R

35. Cilindro
Planificação :
h
x
R

36. Cilindro
Planificação :
h
x
R

37. Cilindro
Planificação :
h
x
R

38. Cilindro
Planificação :
h
x
R

39. Cilindro
Planificação :
h
x
R

40. Cilindro
Planificação :
h
x
R

41. Cilindro
Planificação :
h
x
R

42. Cilindro
Planificação :
h
x
R

43. Cilindro
Planificação :
h
x
R

44. Cilindro
Planificação :
h
x
R

45. Cilindro
Planificação :
h
x
R

46. Cilindro
Planificação :
h
x
R

47. Cilindro
Planificação : R
h
x
R
2 πR R

48. Cilindro Áreas e Volumes
Área Base Ab = π R2
( Ab )
Área Lateral A = 2π Rh
L
( AL )
Área Total
( At ) At = AL+ 2 Ab
Volume
( V) V=πR hR .
2

49. Cilindro
Ex.1:
A base de um cilindro de revolução é equiva-
lente a secção meridiana. Se o raio da base é
unitário, então a altura do cilindro é:
a) π b) 1 c) π d) π e) π
2 2 2
(FUVEST-SP)

50. Cilindro
Ex.2:
Dois cilindros, um de altura 4 e outro de altu-
ra 6, tem para perímetro de suas bases 6 e 4,
respectivamente. Se V1 é volume do primeiro
e V2 o volume do segundo, então:
a) V1 = V2
b) V1 = 2V2
c) V1 = 3V2
d) 2V1 = 3V2
e) 2V1 = V2
(PUC - RS)

51. Cilindro
Ex.3:
Um cilindro eqüilátero está inscrito em um
cubo de volume 27 cm3. Qual o volume do
cilindro?
a) 9π cm3 c) 27π cm3 e) 54π cm3
4 4
b) 27π cm3 d) 27π cm3
8
(UF-PA)